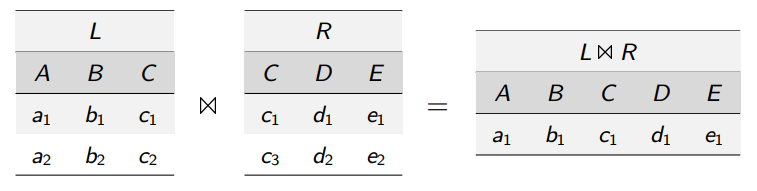Formale Abfragesprachen

Formale Datenbankabfragesprachen (Formal Query Languages)

Theoretische Grundlage für SQL

Alle 3 Sprachen sind gleich mächtig (unter Einschränkung auf sicheren Ausdrücken).

Menge von Tupeln

keine Ordnung

keine Wiederholungen

Relationale Algebra

Manche Operatoren manipulieren ganze Relation, andere nur einzelne Tupel.

Operatoren

Primitive Operatoren

$\sigma$ Selektion

$\pi$ Projektion

$\cup$ Vereinigung

$-$ Differenz

$\times$ Kreuzprodukt

$\rho$ Umbenennung

Ableitbate Operatoren (Syntactic Sugar)

$\bowtie$ join (Natürlicher Verbund)

$⟗$ full outer join

$⟕, ⟖$ left / right full-join

$\rtimes, \ltimes$ left / right semi-join

$\cap$ Durchschnitt

$\div$ Division

$\sigma_{\mathrm{F}}(\mathrm{R })$ Selektion

Wähle alle Tupeln die Formel $\small \mathrm{F}$ erfüllen.

$\operatorname{att}\left(\sigma_{\mathrm{F}}(\mathrm{R})\right)=\operatorname{att}(\mathrm{R})$ Schema von Relation $\small\mathrm{R}$

$\sigma_{\mathrm{F}}(\mathrm{R})=\{t \in R \mid t \text { erfüllt } \mathrm{F}\}$ Ausprägung

$\pi_{A_i}(\mathrm{R})$ Projektion

Wähle alle Attribute $\small A_i$ (und lösche Duplikate).

$\operatorname{att}\left(\pi_{A_{i}}(\mathrm{R})\right)=A_{i}$

$\left\{t^{\prime} \mid \exists t \in \mathrm{R}: t . A_{i}=t^{\prime}\right\}$

In sql stehtselecteigentlich für Projektion und nicht Selektion.

$\mathrm{R} \cup \mathrm{S}$ Vereinigung

Nur wenn Schema von $\small \mathrm{R}$ und $\small \mathrm{S}$ gleich ist: $\small \operatorname{att}(\mathrm{R})=\operatorname{att}(\mathrm{S})$ .

Wähle alle Tupel aus die in $\small \mathrm{R}$ oder $\small \mathrm{S}$ vorkommen.

$\operatorname{att}(\mathrm{R} \cup \mathrm{S})=\operatorname{att}(\mathrm{R})$

$\{t \mid t \in \mathrm{R} \text { oder } t \in \mathrm{S}\}$

$\mathrm{R} - \mathrm{S}$ Differenz

Nur wenn Schema von $\small \mathrm{R}$ und $\small \mathrm{S}$ gleich ist: $\small \operatorname{att}(\mathrm{R})=\operatorname{att}(\mathrm{S})$ .

Wähle alle Tupel die in $\small \mathrm{R}$ aber nicht in $\small \mathrm{S}$ vorkommen

$\operatorname{att}(\mathrm{R} -\mathrm{S})=\operatorname{att}(\mathrm{R})$

$\{t \mid t \in \mathrm{R} \text { und } t \not\in \mathrm{S}\}$

$\mathrm{R} \times \mathrm{S}$ Kreuzprodukt

Gebe alle möglichen Kombinationen von Tupeln aus $\small \mathrm{R}$ und $\small \mathrm{S}$ .

Angenommen: $\small \operatorname{att}(\mathrm{R})=\left(A_{1}, \ldots, A_{m}\right)$ , $\small \operatorname{att}(\mathrm{S})=\left(B_{1}, \ldots, B_{n}\right)$

$\operatorname{att}(\mathrm{R} \times \mathrm{S})=\left(A_{1}, \ldots, A_{m}, B_{1}, \ldots, B_{n}\right)$

$\left\{t_1 \cdot t_2 \mid \exists t_{1} \in \mathrm{R}: t.\left[A_{1}, \ldots, A_{m}\right]=t_{1}\right. \text { und } \left.\exists t_{2} \in \mathrm{S}: t .\left[B_{1}, \ldots, B_{n}\right]=t_{2}\right\}$

Speicherbedarf: $|\mathrm{R}| \cdot |\mathrm{S}|$

Durchschnittlich ist join effizienter als das Kreuzprodukt.

$\rho$ Umbenennung

Umbenennung von Attributen

$\rho_{A \leftarrow B}(\mathrm{R})$

Umbenennung von Relationen

$\rho_{\mathrm{S}}(\mathrm{R})$

$\mathrm{R} \bowtie \mathrm{S}$ Join (natürlicher Verbund)

Bilde $\small \mathrm{R} \times \mathrm{S}$

Finde attribute die doppelt vorkommen und verknüpfe Tupel miteinander die gleichen Attributnamen und Werte haben

Entferne Attribute die doppelt vorkommen mit dem selben Namen
Angenommen
$\mathrm R\left(A_{1}, \ldots, A_{m}, B_{1}, \ldots B_{k}\right)$
$\mathrm S\left(B_{1}, \ldots B_{k}, C_{1}, \ldots C_{n}\right)$
Dann

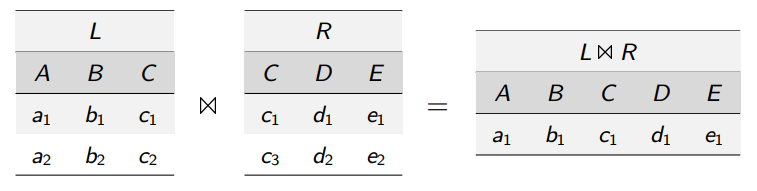
$\mathrm{R} \bowtie_\theta \mathrm{S}$ Join (allgemeiner Verbund)

Keine gleichnamigen attribute notwendig.

$\mathrm R \bowtie_{\theta} \mathrm S=\sigma_{\theta}(\mathrm R \times \mathrm S)$

$\mathrm{R}~ ⟗ ~\mathrm{S}$ full outer join

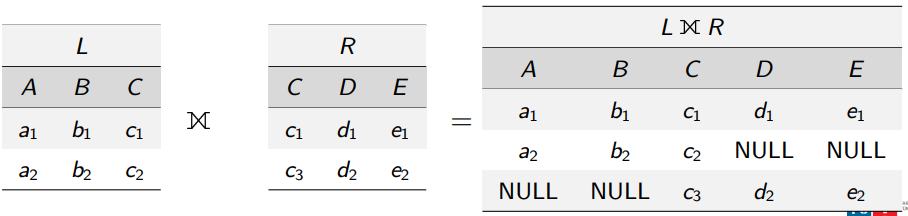
$\mathrm{R}~ ⟕ ~\mathrm{S}$ left full-join

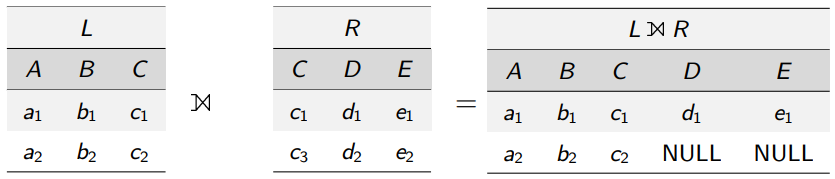
$\mathrm{R~} ⟖\mathrm{~S}$ right full-join

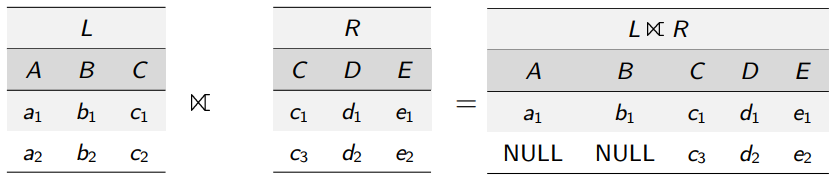
$\mathrm{R}\ltimes\mathrm{S}$ left semi-join

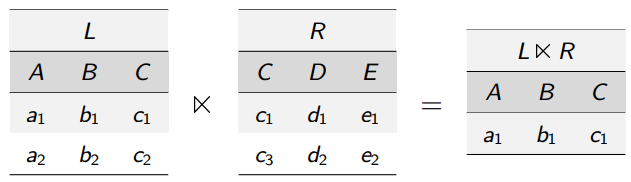
$\mathrm{R} \rtimes \mathrm{S}$ right semi-join

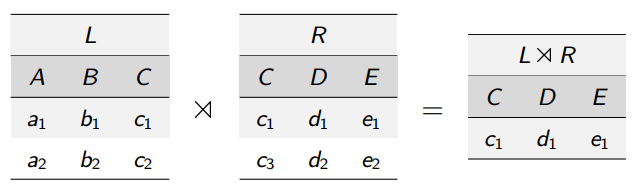
$\mathrm{R} \cap\mathrm{S}$ Durchschnitt

$\mathrm R \cap \mathrm S=\mathrm R-(\mathrm R-\mathrm S)$

$\mathrm{R} \div \mathrm{S}$ Division

Siehe https://de.wikibooks.org/wiki/Relationenalgebra_und_SQL:_Division

$\small \mathrm R$ und $\small \mathrm S$ sind Relationen wobei $\small \operatorname{att}(\mathrm S) \sube \operatorname{att}(\mathrm R)$ .

$t \in \mathrm{R} \div \mathrm{S}$ wenn

$\forall s \in \mathrm S~~\exists r \in \mathrm R: ~~r.\text{att(S)}= s$

Dann nehmen wir für die Tupel diese $r$ (aber entfernen davon die Attribute von $S$ )

$r.(\text{att(R)}-\text{att(S)})= t$

Division lässt sich mit Basisoperationen ausdrücken:

$\mathrm R \div \mathrm S=\pi_{f}(\mathrm R)- \pi_{f}\left(\left(\pi_{f}(\mathrm R) \times \mathrm S\right)-\mathrm R\right)$

$f = {\text{att(R)}-\text{att(S)}}$ Keine Attribute von $\small \mathrm{S}$ in $\small \mathrm{R}$

Syntax

Eine Abfragesprache ist relational abgeschlossen wenn sowohl input als auch output Relationen sind.

Basis-Ausdrücke

Relationen der Datenbank

Konstante Relationen

= nur ein Tupel mit einer Spalte. Kann nur einen Eintrag haben oder keinen Inhalt.

Sind $\small \mathrm R$ und $\mathrm S$ Ausdrücke der relationalen Algebra

dann können rekursiv alle primitiven operatoren auf sie angewendet werden und sie sind weiterhin gültige Ausdrücke.

Relationenkalkül

Formel $\small P(t)$ darf logische, vergleichende Operatoren und Allquantor / Existenzquantor enthalten.

Relationaler Tupelkalkül $\{t \mid P(t)\}$

Relationaler Domänenkalkül $\left\{\left[v_{1}, v_{2}, \ldots, v_{n}\right] \mid P\left(v_{1}, v_{2}, \ldots, v_{n}\right)\right\}$

Sichere Ausdrücke

Keine unendlichen Eingaben oder Ausgaben wie zB

$\{t \mid \neg(t \in R)\}$

$\{[a] \mid \neg([a] \in R)\}$

Definition Sicher

Ein Ausdruck des Tupelkalküls heißt sicher, wenn das Ergebnis des Ausdrucks eine Teilmenge der Domäne ist.

Domäne

Alle Konstanten aus der Formel und Menge aller möglichen Attributwerte.