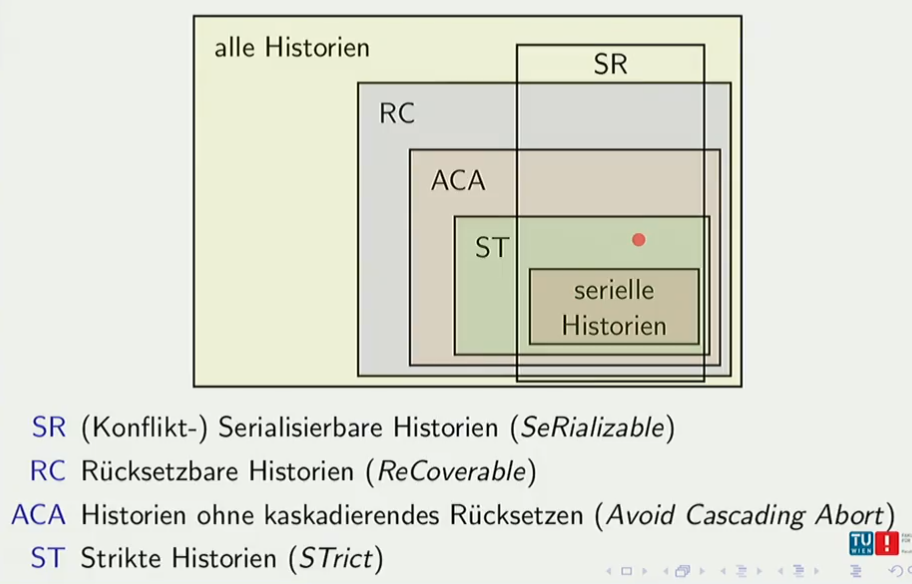
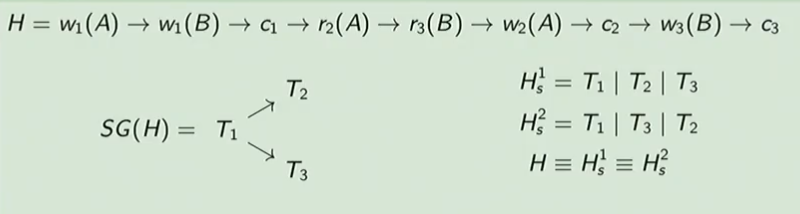Klassifikation von Historien
Je kleiner die Menge, desto eingeschränkter sind die Historien.
konfliktserialisierbar serialisierbar nur ohne
Konflikte
Fehler durch Concurrency wenn auf selben Datensatz zugegriffen wird.
Mindestens eine write-Operation.
- Lost Update
Update durch die erste Schreiboperation geht durch Überschreibung verloren.
- Dirty Read
Datensatz wird gelesen, obwohl es nicht ed wurde.
- DB-Zustand darf während Transaktionen inkonsistent sein.
- Transaktion könnte später ed werden
- Unrepeatable Read
Lese-Operation hat bei mehrfacher Ausführung unterschiedliche Ergebnisse
- Phantomproblem
Gleich aber via
count(*)
Klassifikation von Historien
Transaktion
(steht für die Nummer der Transaktion)
Menge an elementaren Operationen mit partieller Ordnung .
DMBS sieht keine Logik:
Ohne insert und delete.
Ordnung
abort und commit müssen die letzte Aktion sein.
Ordnung muss zwischen allen Operations-Paaren vom selben Datenobjekt definiert sein.
Konflikt-Operation
Paar greift auf das selbe Datenobjekt zu
Historie
Eine mögliche execution-order
Ordnung
Verträglich mit
Ordnung muss zwischen Konfliktoperationen definiert sein.
Seriell
Seriell
sequentielle, ununterbrochene Abarbeitung (eine Transaktion nach dem anderen)
Serialisierbar
Serialisierbar (mit)
Ohne abort sind alle Transaktionen bereits erfolgreich abgeschlossen.
Auswirkung der Historie muss auf jeder konsistenten Ausprägung
... identisch zu einer beliebigen seriellen Historie der selben erfolgreich abgeschlossenen Transaktionen sein
Konflikt-Serialisierbar
Serialisierbarkeit = semantische Definition, nicht syntaktisch. Man müsste zum Überprüfen durchjede konsistente Ausprägungdurchiterieren die es gibt.
Konfliktserialisierbar (conflict serializable)
Konfliktäquivalent zu einer seriellen Historie.
Beispiel
Alle diese Historien sind konfliktäquivalent - die letzte ist eine serielle Historie - dadurch sind alle konfliktserialisierbar.
Sie sind alle über genau 2 Transaktionen und 2 Datenobjekten.
Konflikte sind nur bei Datenobjektmöglich.
Konfliktäquivalenz (conflict equivalence)
von 2 Historien (über die selben, nicht abgebrochenen Transaktionen) wenn
... Reihenfolge von allen Konfliktoperationen gleich ist.
(Reihenfolgeinnerhalbeiner Transaktion darf sich nicht ändern)
Serialisierbarkeits-Theorem
konfliktserilisierbar azyklisch
Jede topologische Sortierung von einem azyklischen ist eine konfliktserialisierbare Historie.
Topologischer Sortierungs-Algorithmus
In jedem azyklischen gerichteten Graphen gibt es mindestens einen Knoten ohne eingehende Kante.
akzyklischer Serialisierbarkeitsgraph
mögliche topologische Sortierung
- wähle Knoten in ohne eingehende Kante
- Schreibe in den Output
- Lösche und alle ausgehenden Kanten
- Falls es noch einen Knoten gibt, gehe zum 1. Schritt
Serialisierbarkeits-Graph
Knoten = abgeschlossene Transaktion
Gerichtete Kante = wenn für min einem Konflikt gilt
Konflikt-Serialisierbar Serialisierbar?
ohne
Konflikt-Serialisierbar Serialisierbar
Nicht umgekehrt: Es gibt serialisierbare Historien die nicht konfliktserialisierbar sind.
mit
Konflikt-Serialisierbar Serialisierbar
Rücksetzbar
Rücksetzbar
Für alle gilt:
Wenn von liest, dann darf nicht vor ed werden.
Transaktion darf nur en wenn alle von denen sie gelesen hat auch ed haben.
Lesen:liest von
Wenn für min ein Datenobjekt genau den Wert liest den geschrieben hat:
a)
schreib-operation vor lese-operation
b)
kein rücksetzen von bevor den Wert gelesen hat
c) dann muss es ein geben
schreib-operation zwischen schreib- und lese-operation rücksetzen
Ohne kaskadierendes Rücksetzen
Dieses Problem hat man bei der logischen Protokollierung nicht, da man Operationen reversieren kann, aber in der Praxis nutzt man physische Protokollierung.
Historie ohne kaskadierendes Rücksetzen
2 mögliche Definitionen:
- Wenn von liest, dann muss gelten: (dann mussed haben)
- Änderungen erst nach zum Lesen freigegeben.

Strikt
Strikte Historie
(Nach jeder schreib-operation muss die Transaktion commited oder aborted werden bevor die nächste Transaktion lesen oder schreibenkann → also auch wenn die nächste Transaktion nicht von der vorherigen liest)
Wenn für ein beliebiges
gilt
dann muss