BCNF⊆3NF⊆2NF⊆1NF
Zerlegung
Es entstehen Anomalien, wenn wir nicht Entities und Relations getrennt speichern.
Deshalb braucht man sinnvolle Zerlegung.
Beispiel
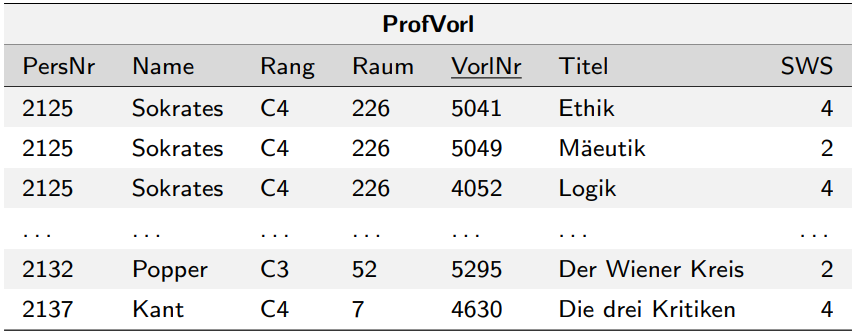
Anomalien
Update-Anomalie Wenn Sokrates umzieht, mehrere Zeilen updaten
Lösch-Anomalie Eine Vorlesung fällt weg
Create-Anomalie kein key, wenn Professor keine Vorlesung ließt
Zerlegung vonRinR1,…,Rn
att(R1)∪⋯∪att(Rn)=att(R)
Kriterien: Verlustlosigkeit und Abhängigkeitstreue
Verlustlostigkeit
Die Informationen in
R
müssen nach der Zerlegung rekonstruierbar sein.
R=πR1(R)⋈πR2(R)⋈⋯⋈πRn(R)
Die Join-Attribute müssen Super-Schlüssel sein.
Abhängigkeitstreue
Die FDs in
R
müssen nach der Zerlegung übertragbar sein.
Sei
R′⊆R
F[R′]={α→β∈F∣α∪β⊆R′}
Es muss gelten
F≡(F+[R1]∪⋯∪F+[Rn])
bzw
F+=(F+
[
R1
]
∪⋯∪F+
[
Rn
]
)+
3. Normalform
Geschichte
1NF: 1. Normalform
Wenn Domänen von
R
atomar sind (keine nested tables)
2NF: 2. Normalform
Wenn nur genau ein einziges Konzept modeliert wird
Definition 3NF
α⊆R
,
B∈R
Wir wandeln alle FDs so um dass rechts nur eine Attribute steht.
∀(α→B)∈F:
muss mindestens eines der Bedingungen gelten:
B∈α
(triviale FD)
α
ist ein Superschlüssel von
R
Attribut
B
ist Teil des Schlüssel von
R
Alternative Definition
💡
Nur damit man die Definition aus Wikipedia auch versteht.
Nicht Teil des Stoffes
Nach Codd: "Es muss 2NF gelten und kein Nicht-Schlüssel-Attribut darf transitiv von einem Schlüssel abhängen"
Das bedeutet - Angenommen es existieren die Attributmengen:
keys, nonKeys
Dann muss gelten:
keys→nonKeys
nonKeys→keys
nonKeys→A,A∈/keys,A∈/nonKeys
Synthese-Algorithmus
Ermöglicht
Zerlegung in 3NF
R=R1∪⋯∪Rn
Verlustlos, Abhängigkeitstreu und alle
Ri
sind in 3NF.
Synthese-Algorithmus
-
Bestimme kanonische Überdeckung
FC
zu
F
Damit wir nur so viel zerlegen wie unbedingt notwendig
- ∀(α→β)∈FC:
Erstelle für jede FD ein eigenes Relationenschema
Ri:=α∪β
Ordne jeder
Ri
die FDs
Fi:=Fc[Ri]
zu
F
C
[Ri]=
{
α→β∈F
C
∣α∪β⊆Ri
}
Damit Abhängigkeitstreue erfüllt ist
-
Falls keines der erzeugten Teilschemata einen Schlüssel von
R
enthält,
-
wähle einen Schlüssel
κ∈R
Keinjoinmöglich, deshalb IDs erzeugen
-
Definiere zusätzlich das Schema
Rκ:=κ
wobei
Fκ:=∅
- Kürze überflüssige Schemata wenn sie in einem anderen enthalten sind.
Boyce-Codd Normalform
Es werden mit 3NF nicht alle Anomalien beseitigt.
Beispiel
R= Sta¨dte(Ort, Land, Chef, EW)
F={{ Ort, Land }→{EW},{ Land }→{ Chef },{ Chef }→{ Land }}
Schlüssel:
{ Ort, Land },{ Ort, Chef }
Redundanz: Wer
chef
von einem
land
ist
Theoretisch weil sie sich gegenseitig bestimmen, müsste nur eines der beiden Attribute vorkommen.
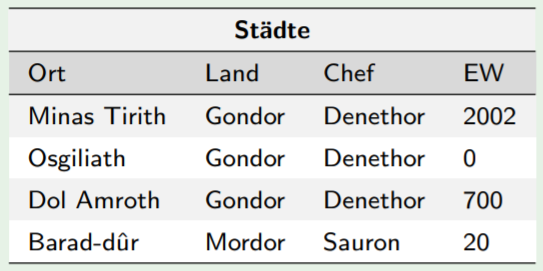
Nur in BCNF wird Anomalie-Freiheit garantiert.
Definition BCNF
α⊆R
,
B∈R
Wir wandeln alle FDs so um dass links nur eine Attribute steht.
∀(α→B)∈F:
muss mindestens eines der Bedingungen gelten:
B∈α
(triviale FD)
α
ist ein Superschlüssel von
R
AttributB∈einem der Schlüssel vonR
Dekompositions-Algorithmus
Ermöglicht
Zerlegung in BCNF
R=R1∪⋯∪Rn
Verlustlos,
Abhängigkeitstreu
und alle
Ri
sind in 3NF.
Es ist nicht immer möglich, dass Zerlegung Abhängigkeitstreu ist.
Dekompositions-Algorithmus
- Z={(R,F)}
- ∀(Ri,Fi)∈Z
:
Wenn nicht in BCNF, dann wähle die
(α→β)∈Fi
welche die Bedingung verletzt
-
Zerlege
Ri
Ri1:=(α∪β)Fi1:=Fi+
[
Ri
1
]
Ri2:=Ri−(β−α)Fi2:=Fi+
[
Ri
2
]
wobeiFi+[Ri]=
{
α→β∈Fi+∣α∪β⊆Ri
}
-
Entferne
(Ri,Fi)
aus
Z
-
Füge
(
Ri1,Fi1
)
und
(
Ri2,Fi2
)
in
Z
ein
Z:=
(
Z−
(
{
Ri,Fi
)
}
)
∪
{
(
Ri
1
,Fi
1
)
}
∪
{
(
Ri
2
,Fi
2
)
}

