Example

Example: Putting on a pair of shoes

$Init()$

$Goal(RightShoeOn \wedge LeftShoeOn)$

$Action(\textcolor{pink}{RightShoe}, \text{PRECOND: }RightSockOn, \text{EFFECT: }RightShoeOn)$

$Action(\textcolor{pink}{RightSock}, \text{EFFECT: }RightSockOn)$

$Action(\textcolor{pink}{LeftShoe}, \text{PRECOND: }LeftSockOn, \text{EFFECT: }LeftShoeOn)$

$Action(\textcolor{pink}{LeftSock}, \text{EFFECT: }LeftSockOn)$

Partial-order planner would come up seperately with:

$[RightSock, RightShoe]$ for goal $RightShoeOn$

$[LeftSock, LeftShoe]$ for goal $LeftShoeOn$

Then these sequences would be combined to construct a final plan.

Every action sequence that maintains the partial order is a solution.

"Every linearisation of a partial-order solution is a total-order solution whose execution from the initial state will reach a goal state."

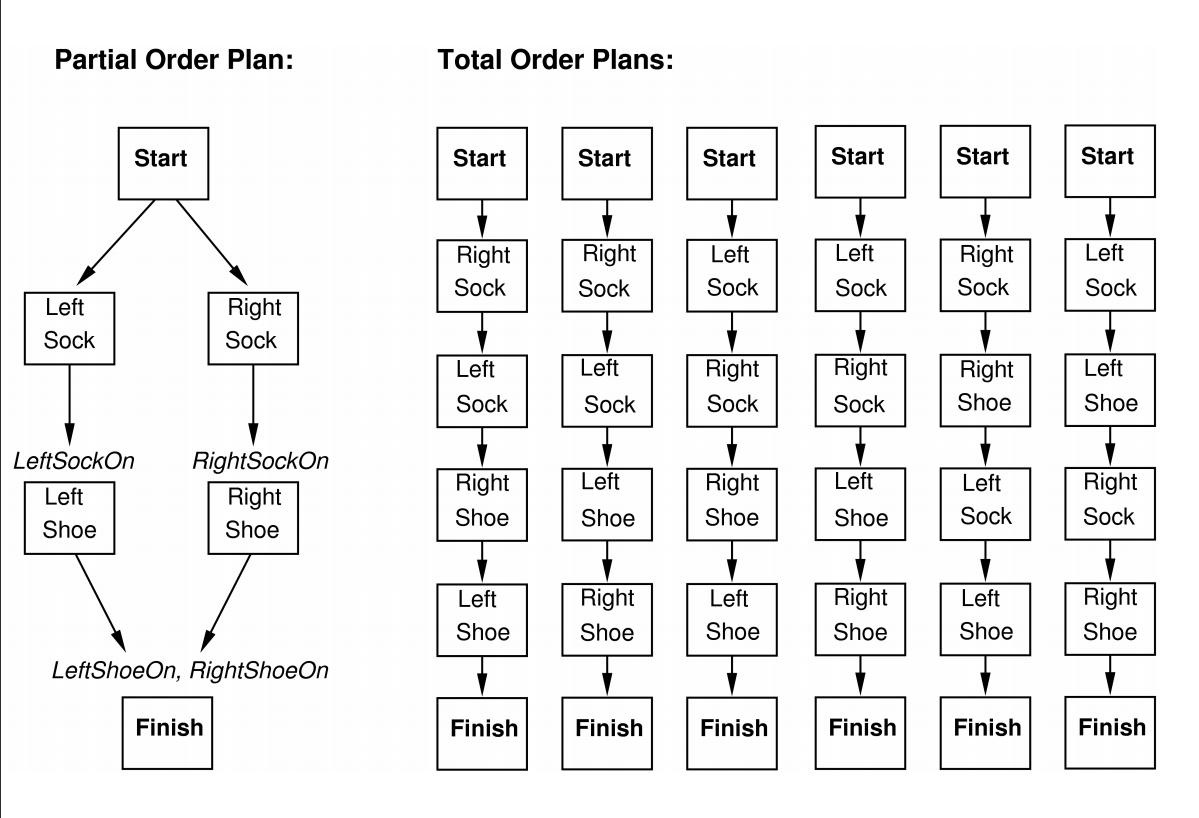
Solution by POP

Actions

$\{RightSock, RightShoe, LeftSock, LeftShoe, Start, Finish\}$

Orderings

$\{ \text{Start} \prec \text {RightSock} \prec \text { RightShoe, Left Sock} \prec \text {LeftShoe} \prec \text{Finish} \}$

Links

$\{\text {RightSock} \stackrel{\text {RightSockOn}}{\longrightarrow} \text {RightShoe, LeftSock} \stackrel{\text {LeftSockOn}}{\longrightarrow} \text { LeftShoe, } \\ \text{RightShoe} \stackrel{\text {RightShoeOn}}{\longrightarrow} \text {Finish, LeftShoe} \stackrel{\text {LeftShoeOn}}{\longrightarrow} \text {Finish}\}$

Open preconditions

$\{\}$