CSP

📎 Examples

Motivation

Until now in search problems: states as a black box.

Constraint satisfaction search problems: space of states with factored representations .

Advantages:

  • Faster search - CSP solvers eliminating space that violates constraits.
  • because its a formal represenation language we can get general purpose heuristics instead of problem specific heuristics

Applications:

  • constrained optimization problem (CSP that uses "objective function")
  • Assignment problems (ie. who teaches what class)
  • Timetabling problems (ie. which class is offered when and where?)
  • Hardware configuration
  • Transportation scheduling

Definition

Variables{X1,…,Xn}\left\{X_{1}, \ldots, X_{n}\right\}

Variable Domains{D1,…,Dn}\left\{D_{1}, \ldots, D_{n}\right\}

Assigned Values{Xi=vi∈Di,Xj=vj∈Dj,…} \left\{X_{i}=\right. \left.v_{i} \textcolor{grey}{\in D_i}, \space X_{j}=v_{j} \textcolor{grey}{\in D_j}, \ldots\right\} 

ConstraintsDi1×⋯×Dij={(d1,…,dj)∣dI∈DiI,1≤I≤j} D_{i_{1}} \times \cdots \times D_{i_{j}}=\left\{\left(d_{1}, \ldots, d_{j}\right) \mid d_{I} \in D_{i_{I}}, 1 \leq I \leq j\right\} 

Is a subset of the cartesian product of the domains - called "goal test"

Unary constraints Restrict value for a single variable.

Binary constraints Relation between two variables - the only type of constraint in binary CSPs

N-ary constraints Higher order constraints / global constraints between multiple variables.

ie:Alldiff{…}\text{Alldiff}\{\dots\}- all variables must have different values

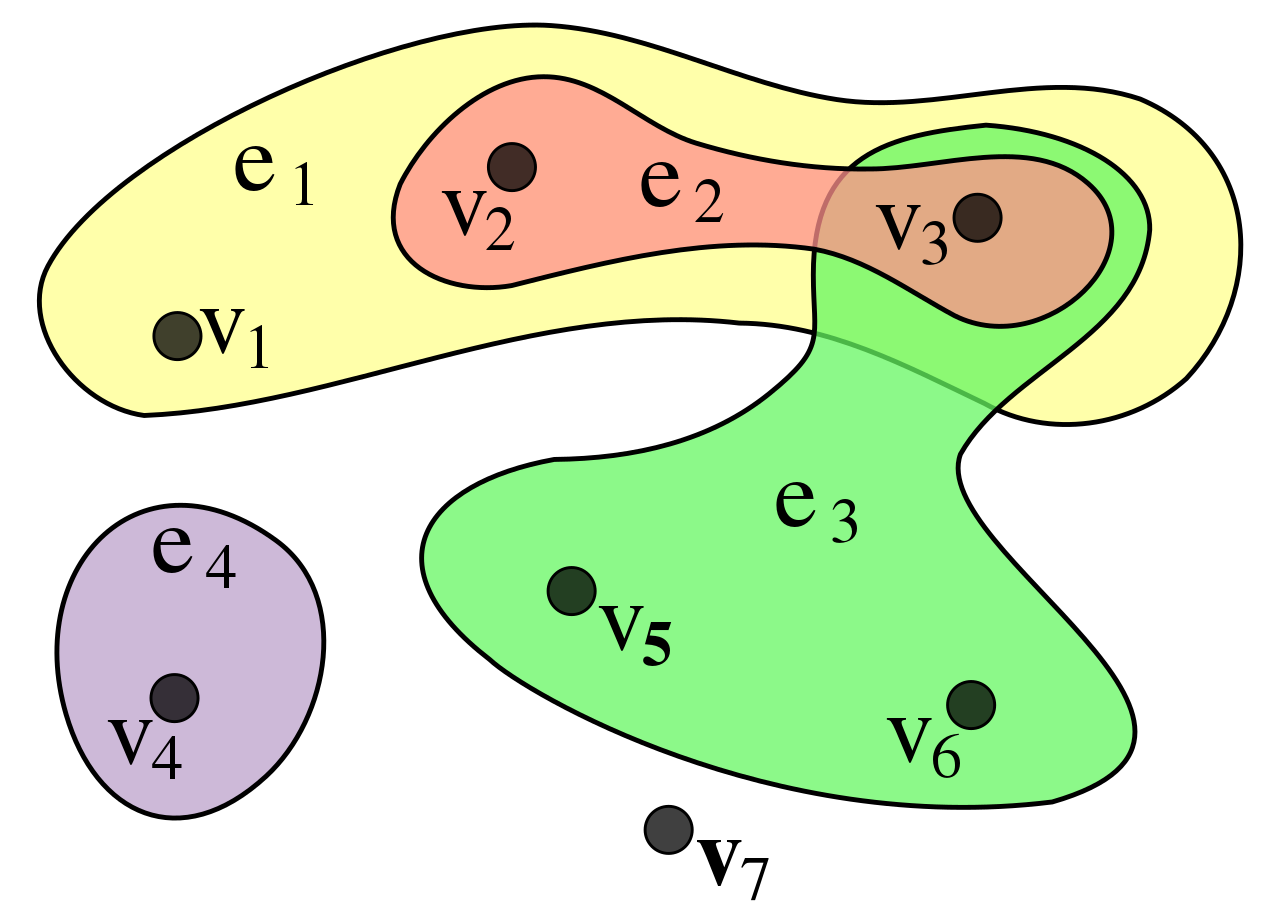
Hyper graph

All higher order constraints can be shown in a hypergraph. (ie. cryptographic puzzles)

In hypergraphs, an edge can join any number of vertices.

  • Example

    X={v1,v2,v3,v4,v5,v6,v7} X=\left\{v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}, v_{7}\right\} 

    E={e1,e2,e3,e4}={{v1,v2,v3},{v2,v3},{v3,v5,v6},{v4}} E=\left\{e_{1}, e_{2}, e_{3}, e_{4}\right\}=\left\{\left\{v_{1}, v_{2}, v_{3}\right\}\right., \left.\left\{v_{2}, v_{3}\right\},\left\{v_{3}, v_{5}, v_{6}\right\},\left\{v_{4}\right\}\right\} 

Hypergraph HH is a pair H=(X,E)H = (X,E) where

XX set of vertices (= nodes)

EE set of non-empty subsets of XX (=hyper-edges)

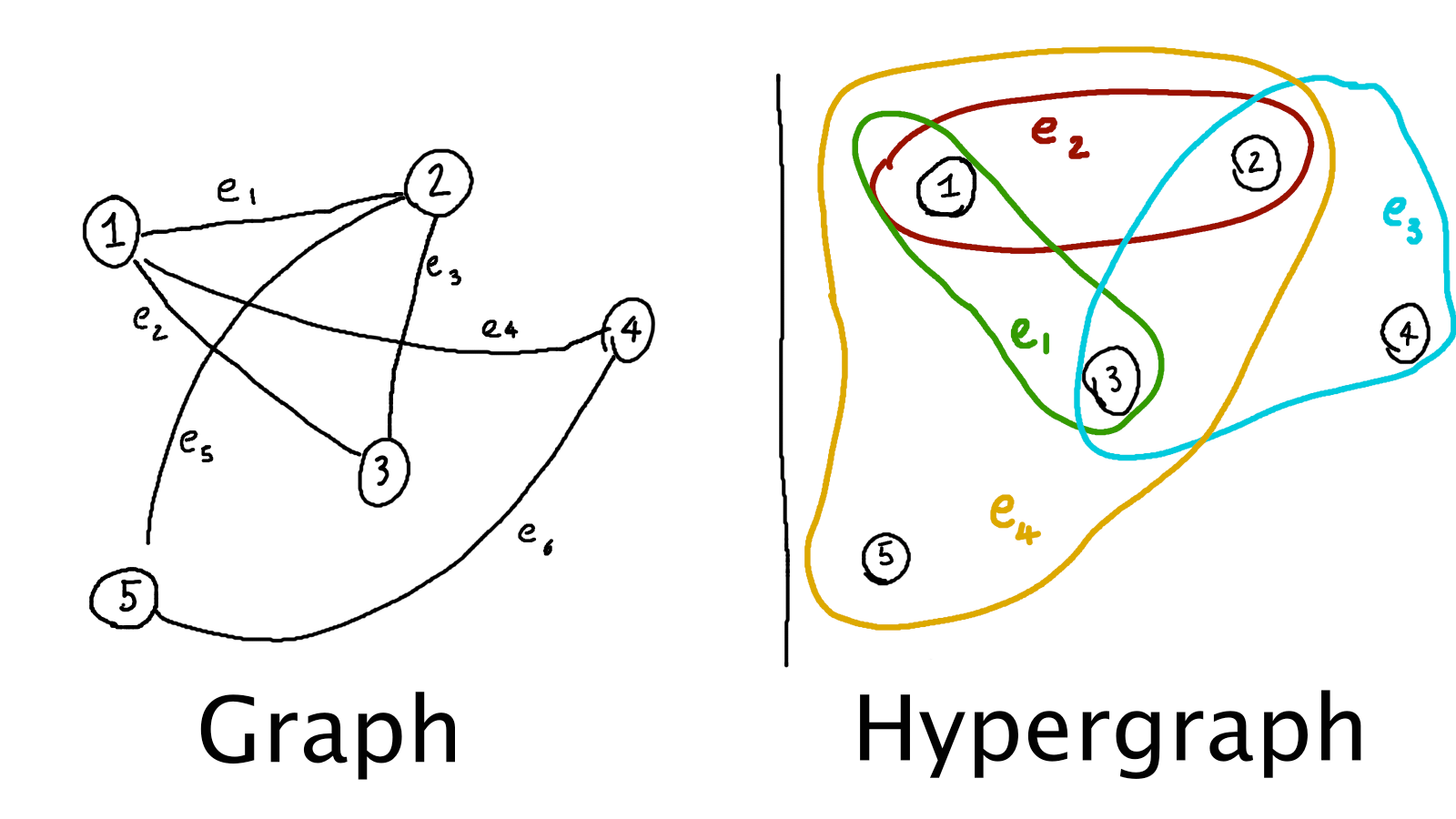
Therefore E⊆P(X)\{∅}E \subseteq \mathcal{P}(X) \backslash \{ \empty \}

Constraint graph

Can only be used for binary CSPs (only have binary constraints)

Types of CSPs

Boolean CSPs

boolean domain - can express 3SAT

3SAT ( ∈\in NP-complete) can be expressed with a boolean CSP.

We cannot solve CSPs in less than exponential time - but in practice they can solve problems a lot bigger than general search algorithms.

Infinite Domains

no enumeration possible.

requires constraint language for linear constraints.

solved with linear programming in polynomial time (non-linear constraints are undecidable).

ie. construction job scheduling

Continuous Domains

Linear / Quadratic Programming Problems.

CSPs as standard search problems

Formulation

Any standard search algorithm can be used to solve CSPs.

Initial state∅\empty

State partial / complete assignment of values to variables

Successor function Assign value to unassigned variable without conflicts

Goal test Do variables satisfy all constraints on them?

Solution Complete assignment satisfying all constraints.

Complexity: not considering commutativity of operations

∣D∣=d,∣X∣=n|D| = d, \quad |X|=n

If we use breadth first search

Branching:

level 0 ndnd branches per node (there is only the empty node)

level 1 (n−1)d(n-1)d branches per node (one variable got an assigned value)

…\dots

level n (n−n)d(n-n)d branches per node (all variables got values assigned to them)

That means that the tree must have n!⋅dnn!\cdot d^n leaves although there are only dnd^n possible complete assignments.

Complexity: considering commutativity of operations

order of value assignment does not matter - gets dnd^n leaves.

We consider a single variable per tree level.

Backtracking search algorithm

Depth-first search with single-variable assignments:

  1. chooses values for one unassigned variable at a time - does not matter which one because of commutativity.
  1. tries all values in the domain of that variable
  1. backtracks when a variable has no legal values left to assign.

General-purpose methods for backtracking search

Since plain backtracking search is an uninformed algorithm, it is not effective for large problems - we need heuristics:

  • In what order should variables be chosen and domains be ordered?
  • which consistency should be checked?
  • can we avoid repeating mistakes?

Value and Variable Ordering

Variable ordering: fail first

  • Minimum remaining (legal) values MRV
  • degree heuristic - (used as a tie breaker), variable that occurs the most often in constraints

Value ordering: fail last

  • least-constraining-value - a value that rules out the fewest choices for the neighbouring variables in the constraint graph.

Consistency

By looking at some of the constraints earlier in the search, or even before the search, the search space can be drastically reduced.

We ensure consistency before or during the search process.

Node consistency

For unary constraints - done before the search.

Forward checking

During search: Adapt domains of all nodes, connected to the value of this one (in constraint graph).

Forward checking does not provide early detection for all inconsistencies:

It only checks arc consistency for the currently chosen node and its neighbours.

NT and SA cannot both be blue!

Constraint Propagation

Propagating the implications of a constraint on one variable onto other variables.

The simplest form: Arc (= binary constraint) Consistency between nodes in a constraint graph.

Two connected nodes X,YX,Y are consistent iff for every value xx of XX there is some allowed value yy of YY .

Intelligent backtracking

We must jump back far enough to reach the node that actually caused the conflict. This occures when every single value is in conflict with current node.

conflict directed backjumping

When we reach a contradiction, backjumping can tell us how far to back up, so we don’t waste time changing variables that won’t fix the problem.

  1. keep conflict set of all assigment that are in conflict with node that we came from.
  1. jump to value from conflict set that has a consistent solution (some dont!) and continue there

Alternative Searches

Local search

very effective: the million-queens problem can be solved in an average of 50 steps

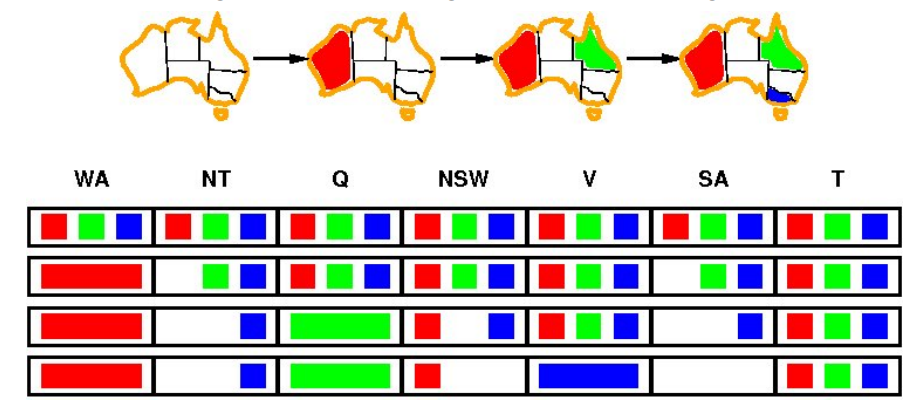
Considering structure of the constraint graph

can be taken into account.