Example

Examples

Example: a)

We want to drive up a mountain and have only two roads (actions) to pick from:

$a_1$ is a nice, straight highway through a low pass.

$a_2$ is a winding dirt road over the top.

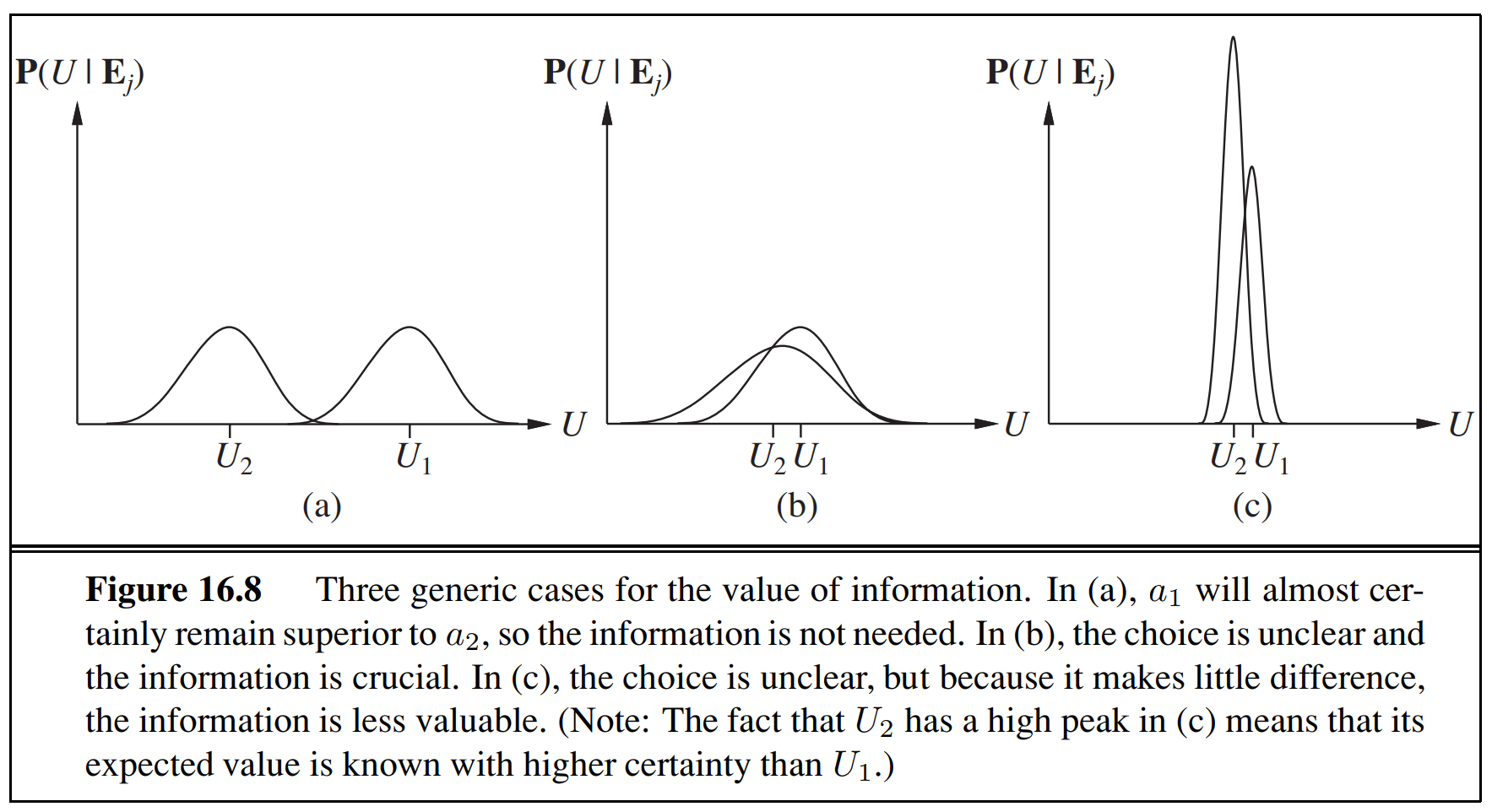
Just given this information, a1 is clearly preferable.

Now we will look at satelite images and gain additional information $e_{j}$ .

Without the information $E_j= e_{j}$

$E U(a_1 \mid \mathbf{e})= \sum_{s} P(\operatorname{RESULT}(a_1)=s \mid a_1, \mathbf{e}) \cdot U(s) = \textcolor{pink}{U_1}$

$E U(a_2 \mid \mathbf{e})= \sum_{s} P(\operatorname{RESULT}(a_2)=s \mid a_2, \mathbf{e}) \cdot U(s) = \textcolor{pink}{U_2}$

Best action $\alpha$ under initital evidence $\mathbf{e}$

$E U(\alpha \mid \mathbf{e})=\max _{a} \sum_{s^{\prime}} P\left(\operatorname{RESULT}(a)=s^{\prime} \mid a, \mathbf{e}\right) \cdot U\left(s^{\prime}\right) = \text{max}(U_1, U_2)$

With the information $E_j= e_{j}$

$E U(a_1 \mid \mathbf{e}, e_{j})=\sum_{s} P(\operatorname{RESULT}(a_1)=s \mid a_1, \mathbf{e}, e_{jk}) \cdot U(s) = \textcolor{pink}{U_1'}$

$E U(a_2 \mid \mathbf{e}, e_{j})=\sum_{s} P(\operatorname{RESULT}(a_2)=s \mid a_2, \mathbf{e}, e_{jk}) \cdot U(s) = \textcolor{pink}{U_2'}$

Best action $\alpha_{e_{jk}}$ after learning

$E U(\alpha_{e_{j}} \mid \mathbf{e}, e_{j})=\max _{a} \sum_{s^{\prime}} P(\operatorname{RESULT}(a)=s^{\prime} \mid a, \mathbf{e}, e_{j}) \cdot U(s^{\prime}) = \text{max}(U_1', U_2')$

Before we obtain the actual value for $E_j$ there will be some probability distribution over the possible (independent) values of $U_1', U_2'$ .

Example: b)

Two different dirt roads of slightly different lengths and we are carrying a seriously injured passenger.

Then, even when $U_1$ and $U_2$ are quite close, the distributions are very broad.

The VPI formula indicates that it might be worthwhile getting the satellite reports.

Example: c)

Finally, suppose that we are choosing between the two dirt roads in summertime, when blockage by avalanches is unlikely.

In this case, satellite reports might show one route to be more beautiful than the other.