Exam on 2012-10-02

1. Formalize a STRIPS action

$\text{Action}(\text{Drive}(car, from, to),$

2. What is a consistent plan? What is a solution?

Solution

The solution to a declared planning-problem is a plan:

Any action sequence that when executed in the initial state - results in a state that satisfies the goal.

Every action sequence that maintains the partial order is a solution.

(The in POP algorithm the goal is therefore only defined by not having open preconditions)

Consistent actions

Chosen actions should not undo the progress made.

Consistent plans (in partial order planning)

Must be free of contradictions / cycles in the ordering constraint set : $(A \prec B) \wedge (B\prec A)$

Must be free of conflicts in the casual links set : precondition $p$ must remain $\text{true}$ if $A \stackrel{p}{\longrightarrow} B$ .

3. Describe the two possible ways to search in the state space search

1. Totally ordered plan searches

   Search in strictly linear order.

   • progression planing: initial state$\rarr$goal
   • regression planing: initial state$\larr$goal

     (possible because of declarative representation of PDDL and STRIPS)

2. Partial-order planning

   Order is not specified.

4. What are the differences between ADL and STRIPS?

5. Risk aversion

Given:

What would the risk averse agent prefer $\text{U}(L)$ or $\text{U}(S_{\text{EMV}(L)})$ ?

Answer:

as we gain more money, its utility does not rise proportionally.

The Utility for getting your first million dollars is very high, but the utility for the additional million is smaller.

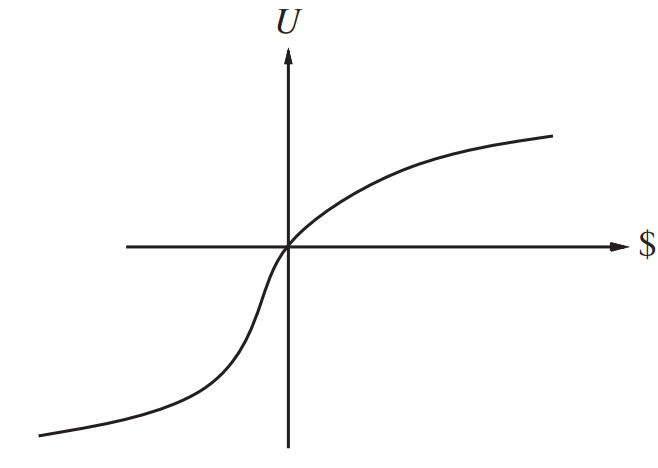
For the risk averse agent:

the utility of being faced with that lottery $<$ than the utility of being handed the expected monetary value of the lottery with absolute certainty

6. The axioms of utility theory

1. Orderability

   The agent must have a preference.

   $(A \succ B) \space \textsf{xor} \space (B \succ B) \space \textsf{xor} \space (A \succsim B)$

2. Transivity

   $(A \succ B) \wedge(B \succ C) \Rightarrow(A \succ C)$

3. Continuity

   If $A \succ B \succ C$ there is a probability $p$ for which the agent would be indifferent to

   getting $B$ with absolute certainty

   or $A$ with probability $p$ and $C$ with $1-p$

   $A \succ B \succ C \Rightarrow \exists p\space[p, A ; 1-p, C] \sim B$

4. Substitutability

   If agent is indifferent to $A$ and $B$ then agent is indifferent to complex lotteries with same probabilities.

   $A \sim B \Rightarrow[p, A ; 1-p, C] \sim[p, B ; 1-p, C]$

5. Monotonicity

   Agent prefers a higher probability of the state that it prefers.

   $A \succ B \Rightarrow(p>q \Leftrightarrow[p, A ; 1-p, B] \succ[q, A ; 1-q, B])$

6. Decomposability

   Compound lotteries can be reduced to simpler ones.

   $[p, A ; 1-p,[q, B ; 1-q, C]] \sim[p, A ;(1-p) q, B ;(1-p)(1-q), C]$

If an agent violates these axioms it will exhibit irrational behaviour.

• Example: intransitive preferences

  $A \succ B \succ C \succ A$

  Agent can be induced to give away all its money:

  Agent has $A$

  1. We offer $A$ + 1 cent for $C$ (agent accepts)

  2. We offer $B$ + 1 cent for $C$ (agent accepts)

  3. We offer $A$ + 1 cent for $B$ (agent accepts)

  We repeat all over again.

  

7. Components of a decision network

Chance nodes (ovals) random variables

Decision nodes (rectangles) points where decision maker has a choice of actions

Utility nodes (diamonds) agent’s utility function

8. How do the nodes get expanded in uninformed search algorithms?

The node expansion is definied by the goal testing (at expansion / at generation) and the used datastructure for the frontier-set.

1. Breadth-first search BFS Frontier as queue.

2. Uniform-cost search UCS Frontier as priority queue ordered by costs.

3. Depth-first search DFS Frontier as stack.

4. Depth-limited search DLS DFS limited with $\ell$ - returns a $\text{cutoff}$ subtree/subgraph.

5. Iterative deepening search IDS Iteratively increasing $\ell$ in DLS to gain completeness.

9. Given admissible heuristics $(h_1, h_2, \dots, h_n)$ . Which one is the best?

Admissibility

Optimistic, never overestimating, never negative.

Dominance

For two admissible heuristics, we say $h_2$ dominates $h_1$ , if:

Therefore we must choose the admissible heuristic that dominates all the others.

10. Admissible heuristics have a problem with graph search. Which one is it? How can this problem be solved?

For the optimality of the A* solution in graphs the heuristic $h(n)$ must be consistent.

If $h(n)$ decreases during optimal path to goal it is discarded by graph-search.

(But in tree search it is not a problem since there is only a single path to the optimal goal).

Solutions to problem:

11. What is inductive learning?

Types of learning

analytical / deductive learning : going from general rule to more specific and efficient rule

Inductive Learning : discovering the general rule from examples

Learning a function from examples (= supervised learning)

the aim is to find a simple hypothesis that is approximately consistent with training examples

Training set (of data points)

Example input-output pairs: $(x_1, y_1), (x_2,y_2), ..., (x_n,y_n)$

Where each $y_i$ was generated by an unknown function$f(x) = y$

Task of agent

Discover a function $h$hypothesis that approximates the true function $f$ .

Learning: search through the hypothesis space$\mathcal{H}$ for one that performs well even for examples beyond the training set.

We say a problem is realizable if the $f\in \mathcal H$ . (We dont always know because the true function is unknown).

Variations

Test set

Measures the accuracy of the hypothesis.

If it performed well one says it generalized well.

If the hypothesis agrees with all the data then it is called a consistent hypothesis .

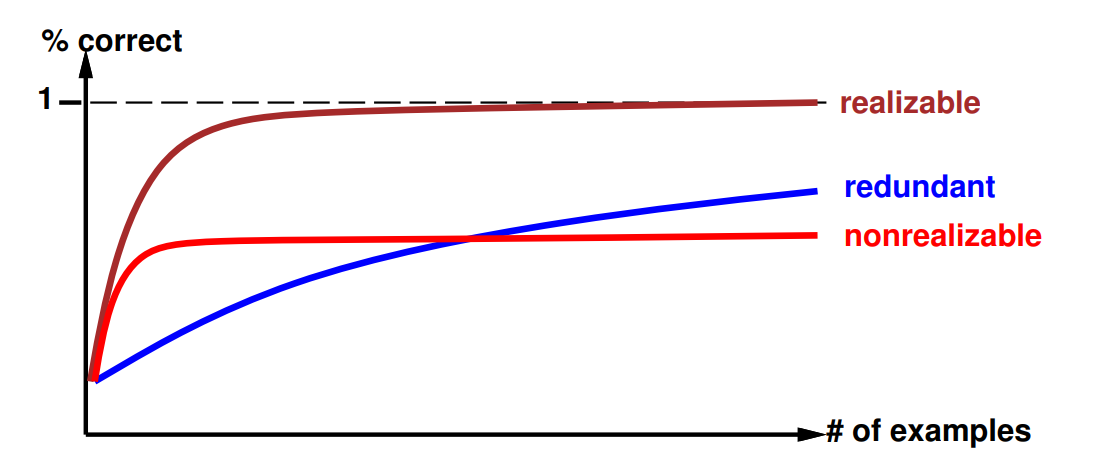
12. What is a learning curve?

How do we know that $h ≈ f$ ? (Hume’s Problem of Induction)

Learning curve = % correct on test set when using $h$

Learning curve depends on realizability of the target function.

Non-realizability can be due to

13. Learning agents and their components

Goal: making agents improve themselves by studying their own experiences

Learning Agent = performance element + learning element

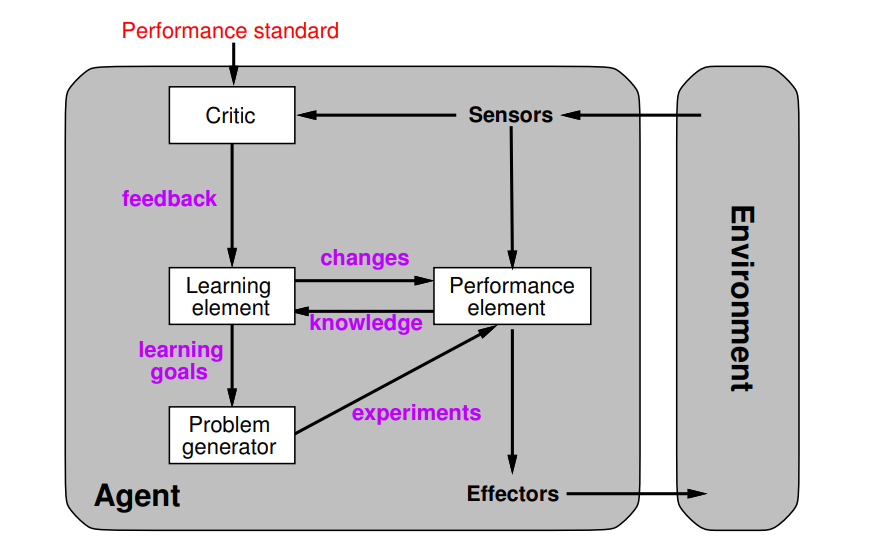
Performance element

Critic

Learning element LE

Problem generator

Example: Taxi

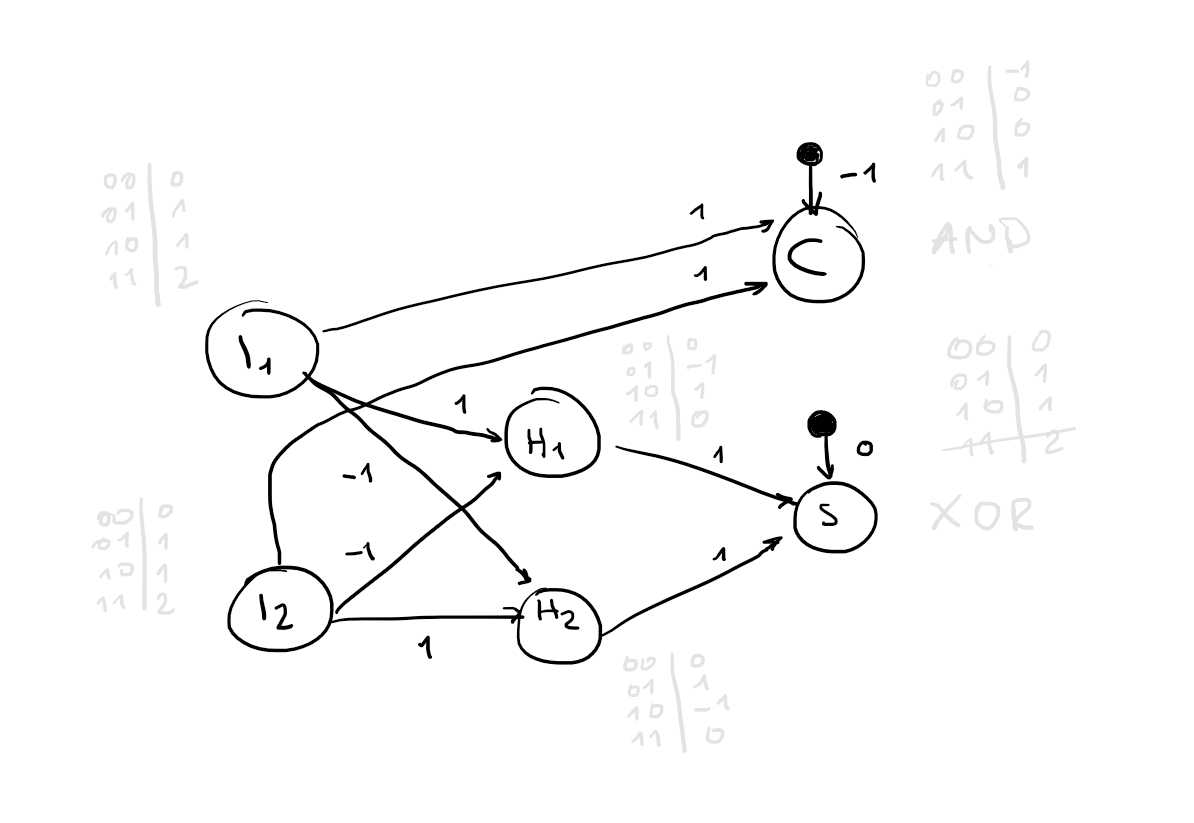
14. Construct a neural network that represents a half adder

• two inputs $I_1, I_2$

• two outputs $C,S$

  where

  $C = I_1 \wedge I_2$

  $S = I_1 \oplus I_2$

Version 1:

Activation function:

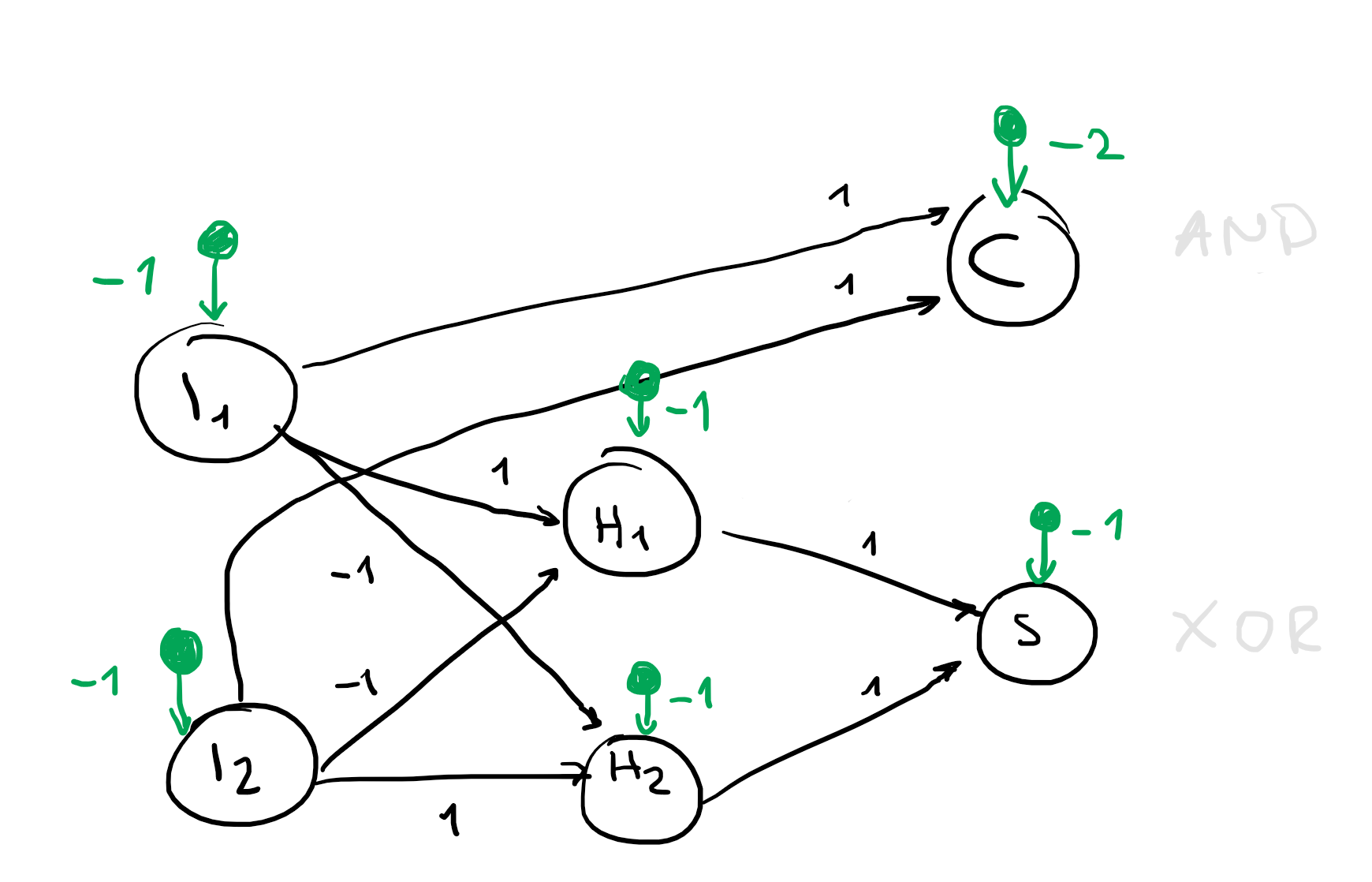
Version 2:

Activation function:

This could be done more elegantly but we just took the previous solution and subtracted $1$ from every nodes weight to be able to copy the previous solution.

15. Advantages and disadvantages of neural networks / learning by observation

Advantages and Disadvantages of Neural Networks

Challenges

• Interpretability

• Explainability

• Trustworthiness

• Robustness (adversarial examples)

• Combining symbolic and subsymbolic approaches