Exam on 2013-07-01

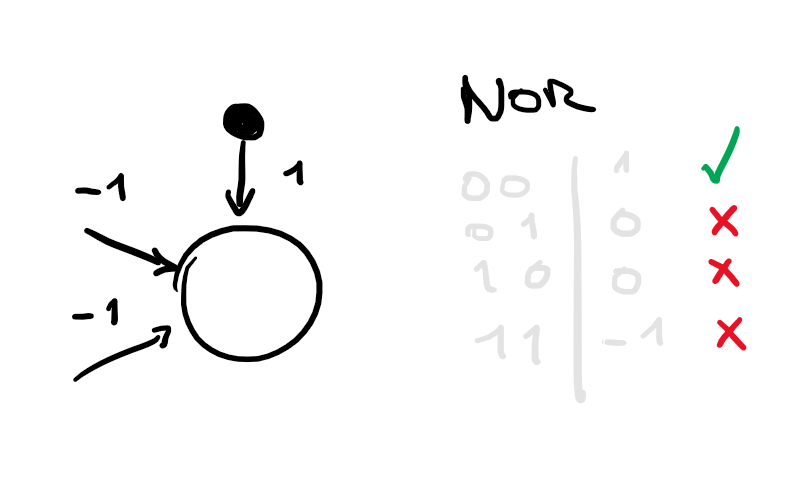
TU_Wien_Einfhrung_in_die_Knstliche_Intelligenz_VU_(Eiter_Tompits)_Prfung_2013-07-01_-_VoWi.pdf

1. Construct a neural network for NOR

Activation function:

$g(x)=\left\{\begin{array}{ll}1 & \text { if } x \geq 1, \\0 & \text { otherwise }\end{array}\right.$

2. What is backwards propagation? How does it work for inner nodes?

Used for multilayer feed-forward neural networks:

We want to minimize the loss (= the sum of gradient losses for all output nodes).

Problem: dependency

We can not learn the weights the same way we did for the single layer network.

The multilayer network has a hidden layer and the output functions are nested functions that contain the nodes behind them.

The error for the hidden layers is not clear - we want to be able to push errors back.

output nodes

Each term in the final summation is computed as if the other outputs did not exist.

Same rule as in the single-layer perceptron.

💡

The index

k

ranges over nodes in the output layer. The index

j

ranges over nodes in the hidden layer.

$\text{Err}_k =$ the $k$ th component of the vector $(\mathbf{y}-\mathbf{h}_{\mathbf{w}}(\mathbf x))$

wj,k←wj,k+α⋅Errk⋅g′(inj)undefined=Δk⋅ajw_{j,k} \leftarrow w_{j,k}+\alpha \cdot \underbrace{ \text{Err}_k \cdot g^{\prime}(in_j)}_{=\Delta_k} \cdot a_{j}wj,k←wj,k+α⋅=ΔkErrk⋅g′(inj)⋅aj

hidden nodes: Back-propagation

We back propagate the errors from the output to the hidden layers.

Δj=g′(inj)∑kwj,k⋅Δk\Delta_{j}=g'(i n_{j}) \sum_{k} w_{j, k} \cdot\Delta_{k}Δj=g′(inj)k∑wj,k⋅Δk

Δj=g′(∑i=0nwi,jai)undefined=g′(inj)⋅∑kwj,k⋅(y−hw(x))k⋅g′(∑iwi,kai)undefined=Δk\Delta_{j}=\underbrace{ g' \bigl( \sum_{i=0}^n w_{i,j}a_i \bigl) }_{=g'(in_j)} \cdot\sum_{k} w_{j, k} \cdot \underbrace{ (\mathbf{y}-\mathbf{h}_{\mathbf{w}}(\mathbf x))_k \cdot g' \bigl( \sum_{i} w_{i,k}a_i \bigl)}_{=\Delta_k}Δj==g′(inj)g′(i=0∑nwi,jai)⋅k∑wj,k⋅=Δk(y−hw(x))k⋅g′(i∑wi,kai)

wi,j←wi,j+α⋅Δj⋅aiw_{i,j} \larr w_{i,j} + \alpha \cdot \Delta_j\cdot a_iwi,j←wi,j+α⋅Δj⋅ai

3. What does the mathematical model of a neuron look like?

McCulloch and Pitts (1943)

The inputs stay the same, only the weights are changed.

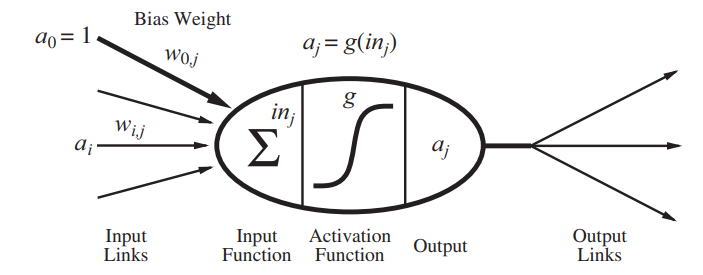
Each unit has a dummy input $a_0 = 1$ with the weight $w_{0,j}$ .

The unit $j$ 's output activation $a_j$ is

aj=g(inj)=g(∑i=0nwi,jai)a_j = g(in_j) = g\biggl( \sum_{i=0}^n w_{i,j}a_i \biggl)aj=g(inj)=g(i=0∑nwi,jai)

Where $g$ is an activation function :

perceptron hard threshhold $g(x)=\left\{\begin{array}{ll}1 & \text { if } x \geq 0 \\0 & \text { otherwise }\end{array}\right.$

sigmoid perceptron logistic function $g(x) = \frac{1}{1+e^{-x}}$

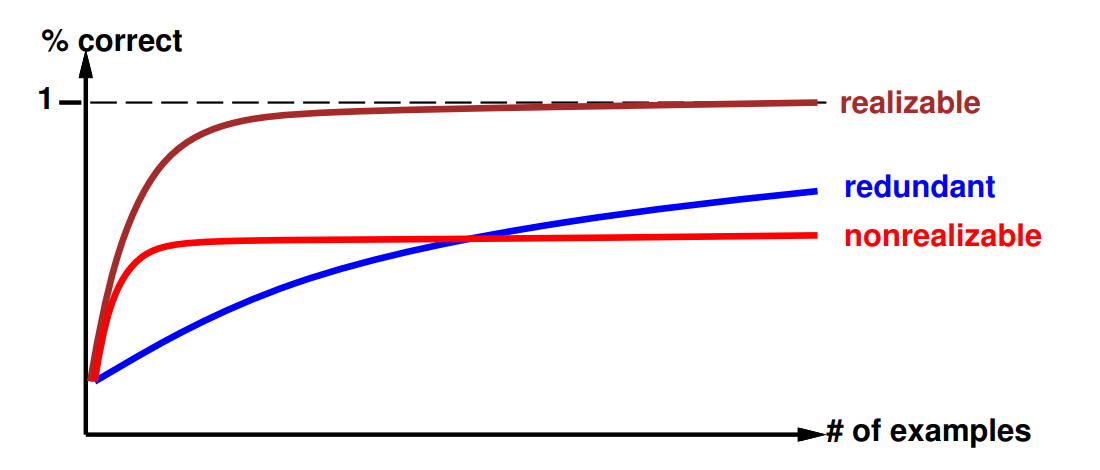
4. What is a learning curve? In which 2 cases is it not optimal?

How do we know that $h ≈ f$ ? (Hume’s Problem of Induction)

Learning curve = % correct on test set when using $h$

Learning curve depends on realizability of the target function.

Non-realizability can be due to

missing attributes

too restrictive hypothesis space (ie. linear function)

redundant expressiveness (ie. loads of irrelevant attributes)

5. What is an admissible or consistent heuristic?

Admissibility

Optimistic, never overestimating, never negative.

$h(n) \leq f^*(n)$

$h(n) \geq 0$

$\forall g$ goals: $h(g)=0$ (follows from the above)

Consistency / Monotonicity

Every consistent heuristic is also admissible. Consistency is stricter than admissibility.

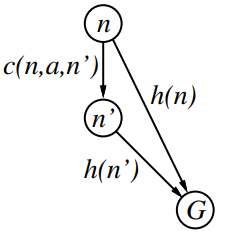
Implies that $f$ -value is non-decreasing on every path .

For every node $n$ and its successor $n'$ :

$h(n) \leq c(n,a,n') + h(n')$

6. Prove the following:

If the heuristic is consistent and $n'$ is the neighbour of $n$ , then $f(n') \geq f(n)$

For every node $n$ and its successor $n'$ :

$h(n) \leq c(n,a,n') + h(n')$

This is a form of the general triangle inequality.

$f$ is then non-decreasing along every path:

$f(n') = g(n') + h(n')= g(n) + {c(n, a,n') + h(n')}$

$f(n') = g(n) + \textcolor{pink}{c(n, a,n') + h(n')} \geq g(n) +\textcolor{pink}{ h(n)} = f(n)$ (because of consistency)

$f(n') \geq f(n)$

7. From a set of admissible heuristics, which one is optimal for search?

For two admissible heuristics, we say $h_2$ dominates $h_1$ , if:

$\forall n: h_2(n) \geq h_1(n)$

Then $h_2$ is better for search.

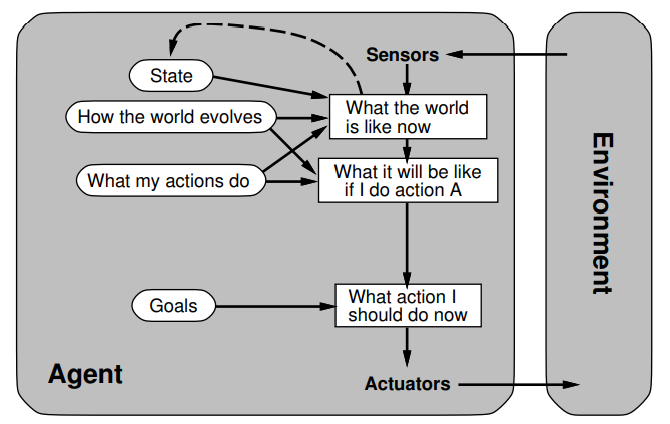
8. What are the components of a goal-based agent?

Goal-based agents

Add on: explicit goals , ability to plan into the future, model outcomes for predictions

model the world , goals, actions and their effects explicitly

more flexible, better maintainability

Search and planning of actions to achieve a goal

9. Draw a CSP from a geographical map

Constraint graph

Can only be used for binary CSPs (only have binary constraints)

10. Define the following heuristics:

General-purpose methods for backtracking search: Since plain backtracking search is an uninformed algorithm, it is not effective for large problems - we need heuristics.

Variable ordering: fail first

Minimum remaining (legal) values MRV

degree heuristic - (used as a tie breaker), variable that occurs the most often in constraints

Value ordering: fail last

least-constraining-value - a value that rules out the fewest choices for the neighbouring variables in the constraint graph.

11. Are nonlinear CSPs always decidable?

No they are undecidable.

Infinite Domain CSPs

no enumeration possible.

requires constraint language for linear constraints.

solved with linear programming in polynomial time (non-linear constraints are undecidable).

ie. construction job scheduling

Continuous Domains CSPs

Linear / Quadratic Programming Problems.

12. Does a CSP with $n$ variables and $d$ values in its domain have $O(d^n)$ possible assignemnts?

Yes - this is because we are considering the commutativity of operatins and pick a single variable to assign for each tree level.

13. Construct a STRIPS action

A cyclist wants to move from A to B.

$\text{Action}(\text{Cycle}(bicylcle, from, to),$

$\text{PRECOND:}~\text{At}(bicycle, from)\wedge \text{Bicycle}(bicycle) \wedge \text{Location}(from) \wedge \text{Location}(to)$

$\text{EFFECT:} ~\text{At}(bicycle, to) \wedge \neg\text{At}(bicycle, from)~~)$

14. STRIPS vs. ADL

STRIPS: conjunctions in goals supported?

Yes - but only non-negative literals

ADL: Are non-occuring predicates wrong?

No - closed-world-assumption means unmentioned literals are false

But ADL supports the open-world-assumption: unmentioned literals are unknown

ADL: is the equiality symbol supported?

Yes - equality and types built in

15. What is the qualification problem?

qualification problem ... what are preconditions for actions?

The inability to capture everything in a set of logical rules

Deals with a correct conceptualisation of things (no answer).

Restrictions of ADL and STRIPS

cant derive other effects from more complex ones

classical planning systems do not attempt to address the qualification problem