Exam on 2017-06-27

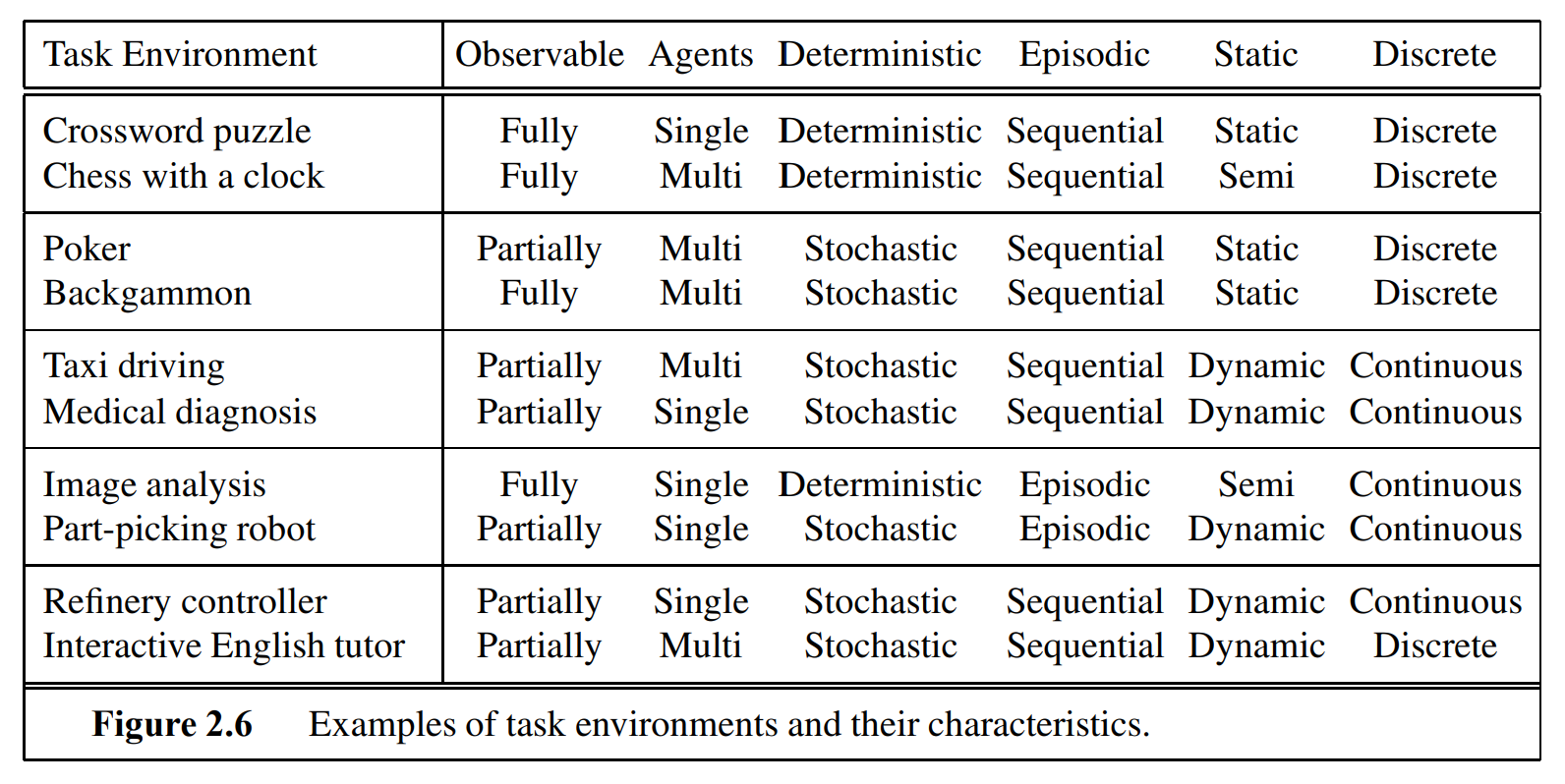
TU_Wien_Einfhrung_in_die_Knstliche_Intelligenz_VU_(Eiter_Tompits)_Prfung_2017-06-27_-_VoWi.pdf

1. Explain the hill climbing algorithm

Also called "hill-climbing":

$+$ escaping shoulders

$-$ getting stuck in loop at local maximum

Solution: Random-restart hill climbing: restart after step limit overcomes local maxima

Pseudocode

function HILL-CLIMBING(problem) returns a state that is a local maximum
inputs: problem // a problem
local variables:
current, // a node
neighbor // a node
current ← MAKE-NODE(INITIAL-STATE[problem])
loop do
neighbor ← a highest-valued successor of current
if VALUE[neighbor] ≤ VALUE[current] then return STATE[current]
current ← neighbor

2. What is an order constraint and when does it lead to problems?

$A \prec B$ Action $A$ must be executed before action $B$ .

Must be free of contradictions/cycles : $(A \prec B) \wedge (B\prec A)$

else we have a problem.

3. What does it mean for a heuristic to be consistent?

What properties do the constants $a,b \geq0$ need to have if $h(n)=a\cdot h_1(n)+ b\cdot h_2(n)$ and $h_1, h_2$ are consistent?

definition of consistency
Every consistent heuristic is also admissible. Consistency is stricter than admissibility.
Implies that $f$ -value is non-decreasing on every path .
For every node $n$ and its successor $n'$ :
$h(n) \leq c(n,a,n') + h(n')$
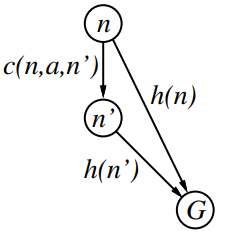
This is a form of the general triangle inequality.
$f$ is then non-decreasing along every path:
$f(n') = g(n') + h(n')= g(n) + {c(n, a,n') + h(n')}$
$f(n') = g(n) + \textcolor{pink}{c(n, a,n') + h(n')} \geq g(n) +\textcolor{pink}{ h(n)} = f(n)$ (because of consistency)
$f(n') \geq f(n)$

$h(n)=a\cdot h_1(n)+ b\cdot h_2(n)$

We want the following inequality to be true so that $h(n)$ stays consistent as the sum of two consistent heuristics with weights $a,b$ :

$h(n)\leq a \cdot \bigg(c(n,a,n') + h_1(n')\bigg)+ b\cdot \bigg( c(n,a,n') + h_2(n')\bigg)$

$h(n)\leq a \cdot c(n,a,n') +a \cdot h_1(n')+ b\cdot c(n,a,n') + b \cdot h_2(n')$

$h(n)\leq a \cdot c(n,a,n') +b\cdot c(n,a,n') + \underbrace{a \cdot h_1(n')+ b \cdot h_2(n')}_{h(n)}$

$h(n)\leq c(n,a,n')\cdot (a+b) + h(n)$

Then $h(n)$ is consistent with any $a, b \geq 0$ .

4. Describe 4 different types of environments that agents can be situated in.

fully observable vs. partly observable

whether sensors can detect all relevant properties

single-agent vs. multi-agent

single agent, or multiple with cooperation, competition

deterministic vs. non deterministic

whether the next state can be determined by current state + the performed action or is fully independent and can't be foreseen (multiple possible following states).

stochastic

whether we know the probabilities of occurences

episodic vs. sequential

Episodic: the choice of action only depends on the current episode - percept history divided into independent episodes.

Sequential: storing entire history (accessing memories lowers performance)

static vs. dynamic vs. semi-dynamic

Static: world does not change during the reasoning / processing time of the agent (waits for agents response)

Semi-dynamic: environment is static, but performance score decreases while processing time.

discrete vs. continuous

property values of the world

known vs. unknown

state of knowledge about the "laws of physics" of the environment

Examples

5. Perceptron learning rule

Inputs $I_1,I_2$

Output $O$

Bias $1$

Learning rate $\alpha =1$

Identity function

The perceptron learning rule:

wi←wi+α⋅(y−hw(x))⋅g′(ini)⋅xiw_i\larr w_i + \alpha \cdot (y-h_{\mathbf{w}}(\mathbf{x})) \cdot g^{\prime}(i n_i) \cdot x_{i}wi←wi+α⋅(y−hw(x))⋅g′(ini)⋅xi

We need the derivative of the identity function $f(x) = x$ :

$f'(x) = 1$

Therefore

wi←wi+α⋅(y−hw(x))⋅1⋅xiw_i\larr w_i + \alpha \cdot (y-h_{\mathbf{w}}(\mathbf{x})) \cdot \textcolor{pink}1 \cdot x_{i}wi←wi+α⋅(y−hw(x))⋅1⋅xi

wi←wi+α(y−hw(x))⋅xiw_i \larr w_i + \alpha(y-h_{\mathbf{w}}(\mathbf{x})) \cdot x_iwi←wi+α(y−hw(x))⋅xi

6. CSP Problem

4 variables with different domains

$A$ ...

$B$ with domain $D_B=\{1,2,5\}$

$C$ with domain $D_C=\{2,3,4,5\}$

$D$ ....

5 constraints

$C_1(A,B)=\{(1,5),(3,4),(2,1),\dots)\}$

$C_2(A,C)=\{\dots\}$

Draw a constraint graph.

How would you pick the next variable / value with <heuristic name> if we assign the value $5$ to $A$ ?

7. Construct a STRIPS action

We want to transfer a file between 2 harddrives.

$\text{On}(x, y)$ $x$ is on $y$

$\text {File}(x)$ $x$ is a file

$\mathrm{HD}(x)$ $x$ is a harddrive

$\text{Empty}(x)$ $x$ is empty

Preconditions:

$A$ contains file

$B$ is empty

both $A, B$ are harddrives

Effect:

$B$ is not empty anyymore

both $A, B$ contain the data

$\text{Action(} Transfer(x,y, file)$

$\text{PRECOND:} ~\mathrm{HD}(x) \wedge \mathrm{HD}(y) \wedge \text {File}(file) \wedge \text{On}(file, x) \wedge \text{Empty}(y) \wedge \neg \text{On}(file,y)$

$\text{EFFECT:}~ \text{On}(file,y ) \wedge \neg \text{On}(file,x) \wedge \text{Empty}(x)~)$

8. Formal description of a search problem

Real World → Search problem → Search Algorithm

We define states, actions, solutions (= selecting a state space) through abstraction.

Then we turn states into nodes for the search algorithm.

Solution

A solution is a sequence of actions leading from the initial state to a goal state.

Initial state

Successor function

Goal test

path cost (additive)

9. Ramification problem, qualification problem - describe and give an example

Reasoning about the results of actions

frame problem ... what are things that stay unchanged after action?

would require a lot of axioms to describe.

ramification problem ... what are the implicit effects?

ie.: passengers of a car move with it

qualification problem ... what are preconditions for actions?

deals with a correct conceptualisation of things (no answer).

ie.: finding the right formalization of a human conversation

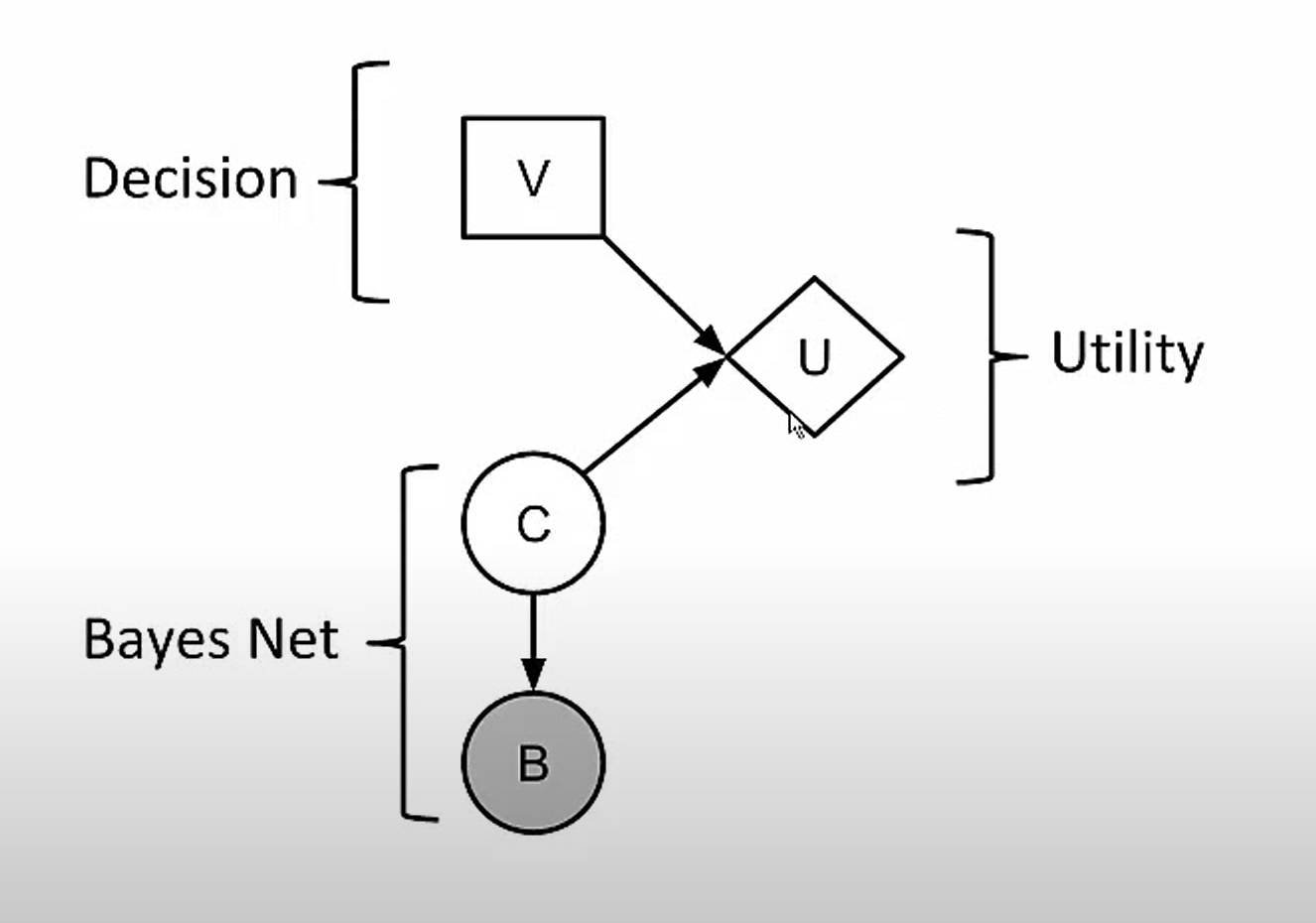
10. Decision Network, define node types

= influence diagrams.

General framework for rational decisions - return the action with highest utility.

Decision networks are an extension of Bayesian networks.

Presents:

current state

possible actions

resulting state from actions

utility of each state

Node types:

Chance nodes (ovals)
Random variables, uncertainty - Bayes Network

Decision nodes (rectangles)
Decision maker has choice of action

Utility nodes (diamonds)
Utility function

11. Why is entropy relevant for decision trees? How is $H(p_1,p_2)$ defined?

Information gain measured with entropy

Entropy measures uncertainty of the occurence of a random variable in [shannon] or [bit].

Entropy of a random variable $A$ with values $v_k$ each with probability $P(v_k)$ is defined as:

H(A)=∑kP(vk)log⁡2(1P(vk))=−∑kP(vk)log⁡2(P(vk))H(A) = \sum_k P(v_k)\log_2 \biggl( \frac{1}{P(v_k)} \biggl)= - \sum_k P(v_k)\log_2(P(v_k))H(A)=k∑P(vk)log2(P(vk)1)=−k∑P(vk)log2(P(vk))

Entropy is at its maximum when all outcomes are equally likely.

💡

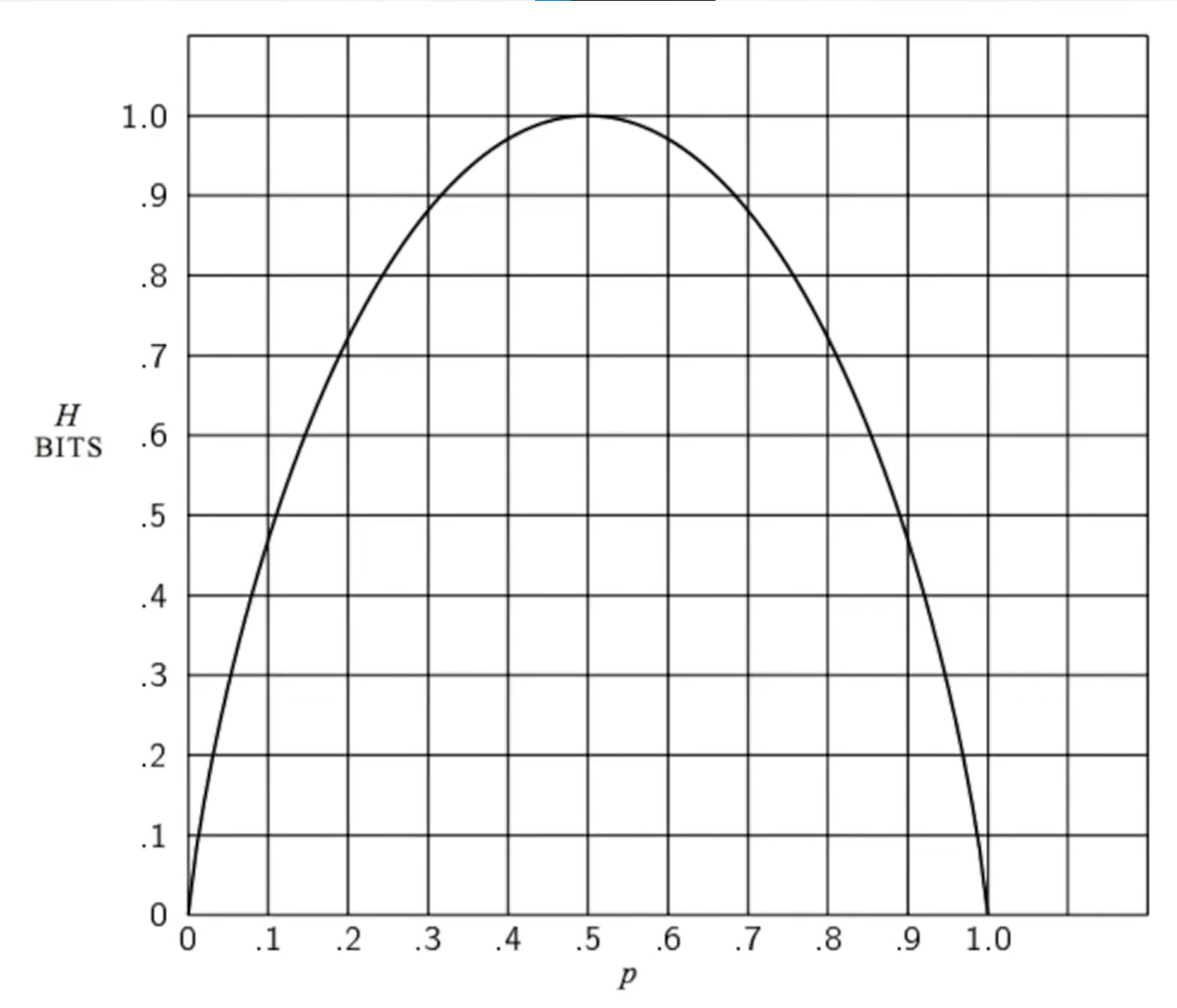
With lower entropy, we can ask fewer questions to get to a decision.

Entropy of a boolean random variable

Boolean random variable $V$ : Variable is true with probability $q$ and false with $(1-q)$ .

Same formula as above.

B(q)=−(q⋅log⁡2(q)+(1−q)⋅log⁡2(1−q))B(q)=-(q\cdot \log_2(q)+(1-q)\cdot \log_2(1-q))B(q)=−(q⋅log2(q)+(1−q)⋅log2(1−q))

12. Multiple Choice part

Does BFS expand as least as often as it has nodes?

This depends on whether we test our goals on generation or on expansion.

Goal test at generation time: $1 + b + b^2 + b^3 + ... + b^d = O(b^d)$

Goal test at expansion time: $1 + b + b^2 + b^3 + ... + b^d + \textcolor{pink}{b^{d+1}}= O(b^{d+1})$

Can BFS be solved with a special case of A*?

No because BFS does not use a priority queue while A* does so.

Is local beam search a modification of the generic algorithm with cross-over?

No - Genetic algorithms GA is a modification of local beam search.

It uses Stochastic local beam search + successors from pairs of states.

Does STRIPS support the notation for equality?

No it doesn't - ADL does.

Does the POP algorithm only produce consistent plans?

Yes - because only consistent plans are generated the goal test is checking if any preconditions are open. If the goal is not reached it adds successor states.