Examples Example: Air cargo transport Initial value and goal state
I n i t ( A t ( C 1 , S F O ) ∧ At ( C 2 , J F K ) ∧ A t ( P 1 , S F O ) ∧ A t ( P 2 , J F K ) ∧ Cargo ( C 1 ) ∧ Cargo ( C 2 ) ∧ Plane ( P 1 ) ∧ Plane ( P 2 ) ∧ Airport ( J F K ) ∧ Airport ( S F O ) )
\textcolor{pink}{Init}\left(A t\left(C_{1}, S F O\right) \wedge \operatorname{At}\left(C_{2}, J F K\right)
\wedge A t\left(P_{1}, S F O\right) \wedge A t\left(P_{2}, J F K\right)\right. \\\quad \wedge
\operatorname{Cargo}\left(C_{1}\right) \wedge \operatorname{Cargo}\left(C_{2}\right) \wedge \text
{Plane}\left(P_{1}\right) \wedge \text {Plane}\left(P_{2}\right) \\\quad \wedge \text {Airport}(J F K)
\wedge \text {Airport}(S F O))
I ni t ( A t ( C 1 , SFO ) ∧ At ( C 2 , J F K ) ∧ A t ( P 1 , SFO ) ∧ A t ( P 2 , J F K ) ∧ Cargo ( C 1 ) ∧ Cargo ( C 2 ) ∧ Plane ( P 1 ) ∧ Plane ( P 2 ) ∧ Airport ( J F K ) ∧ Airport ( SFO ))
G o a l ( A t ( C 1 , J F K ) ∧ At ( C 2 , S F O ) )
\textcolor{pink}{Goal}\left(A t\left(C_{1}, J F K\right) \wedge \operatorname{At}\left(C_{2}, S F
O\right)\right)
G o a l ( A t ( C 1 , J F K ) ∧ At ( C 2 , SFO ) )
Actions:
Loading cargo from airport to plane
Action ( L o a d ( c , p , a ) , PRECOND: A t ( c , a ) ∧ At ( p , a ) ∧ Cargo ( c ) ∧ Plane ( p ) ∧ Airport ( a ) EFFECT: ¬ A t ( c , a ) ∧ In ( c , p ) )
\text {Action }(\textcolor{pink}{Load}(c, p, a), \\ \qquad \text {PRECOND: } A t(c, a) \wedge
\operatorname{At}(p, a) \wedge \operatorname{Cargo}(c) \wedge \text { Plane }(p) \wedge
\operatorname{Airport}(a) \\ \qquad \text {EFFECT: } \neg A t(c, a) \wedge \operatorname{In}(c, p))
Action ( L o a d ( c , p , a ) , PRECOND: A t ( c , a ) ∧ At ( p , a ) ∧ Cargo ( c ) ∧ Plane ( p ) ∧ Airport ( a ) EFFECT: ¬ A t ( c , a ) ∧ In ( c , p ))
Unloading cargo from plane to airport
Action ( U n l o a d ( c , p , a ) , PRECOND: In ( c , p ) ∧ At ( p , a ) ∧ Cargo ( c ) ∧ Plane ( p ) ∧ Airport ( a ) EFFECT: A t ( c , a ) ∧ ¬ In ( c , p ) )
\text {Action }(\textcolor{pink}{Unload}(c, p, a), \\ \qquad \text {PRECOND: } \operatorname{In}(c, p)
\wedge \operatorname{At}(p, a) \wedge \operatorname{Cargo}(c) \wedge \operatorname{Plane}(p) \wedge
\operatorname{Airport}(a) \\ \qquad \text {EFFECT: } A t(c, a) \wedge \neg \operatorname{In}(c, p))
Action ( U n l o a d ( c , p , a ) , PRECOND: In ( c , p ) ∧ At ( p , a ) ∧ Cargo ( c ) ∧ Plane ( p ) ∧ Airport ( a ) EFFECT: A t ( c , a ) ∧ ¬ In ( c , p ))
Flying plane
Action ( F l y ( p , from, to ) ) , PRECOND: A t ( p , from ) ∧ Plane ( p ) ∧ Airport ( from ) ∧ Airport ( t o ) EFFECT: ¬ A t ( p , from ) ∧ A t ( p , to ) )
\operatorname{Action}(\textcolor{pink}{Fly}(p, \text { from, to})), \\ \qquad \text {PRECOND: } A t(p, \text
{from}) \wedge \text {Plane}(p) \wedge \text {Airport}(\text {from}) \wedge \operatorname{Airport}(t o) \\
\qquad \text {EFFECT: } \neg A t(p, \text {from}) \wedge A t(p, \text {to}) \text {)}
Action ( Fl y ( p , from, to )) , PRECOND: A t ( p , from ) ∧ Plane ( p ) ∧ Airport ( from ) ∧ Airport ( t o ) EFFECT: ¬ A t ( p , from ) ∧ A t ( p , to ) )
The following plan is a solution to the problem:
[ Load ( C 1 , P 1 , S F O ) , Fly ( P 1 , S F O , J F K ) , Unload ( C 1 , P 1 , J F K ) Load ( C 2 , P 2 , J F K ) , F Fly ( P 2 , J F K , S F O ) , Unload ( C 2 , P 2 , S F O ) ]
\begin{array}{r}{\left[\operatorname{Load}\left(C_{1}, P_{1}, S F O\right), \text { Fly }\left(P_{1}, S F O,
J F K\right), \text { Unload }\left(C_{1}, P_{1}, J F K\right)\right.}
\\\left.\operatorname{Load}\left(C_{2}, P_{2}, J F K\right), F \operatorname{Fly}\left(P_{2}, J F K, S F
O\right), \text { Unload }\left(C_{2}, P_{2}, S F O\right)\right]\end{array}
[ Load (
C
1 ,
P
1 , SFO ) , Fly (
P
1 , SFO , J F K ) , Unload (
C
1 ,
P
1 , J F K ) Load ( C 2 , P 2 , J F K ) , F Fly ( P 2 , J F K , SFO ) , Unload ( C 2 , P 2 , SFO ) ]
Example: Spare Tire Problem
There are just four actions: removing the spare from the trunk, removing the flat tire from the axle, putting the spare on the axle, and
leaving the car unattended overnight. We assume that that the effect of leaving the tire overnight is that the tires disappear.
Initial value and goal state
Init(Tire(Flat) ∧ Tire ( Spare ) ∧ At ( Flat, Axle ) ∧ At ( Spare, Trunk ) )
\text {Init(Tire(Flat)} \wedge \text {Tire}(\text {Spare}) \wedge \operatorname{At}(\text {Flat, Axle})
\wedge \text {At}(\text {Spare, Trunk}))
Init(Tire(Flat) ∧ Tire ( Spare ) ∧ At ( Flat, Axle ) ∧ At ( Spare, Trunk ))
Goal ( At ( Spare, Axle ) ) \operatorname{Goal}(\text {At }(\text { Spare, Axle })) Goal ( At ( Spare, Axle ))
Actions:
Removing Tire
Action ( Remove ( obj,loc ) , PRECOND: At ( obj , loc ) EFFECT: ¬ At ( obj, loc ) ∧ At ( obj, Ground ) )
\text {Action}(\text {Remove}(\text {obj,} \text {loc}), \\ \qquad \text {PRECOND: } \text{At}(\text {obj},
\text {loc}) \\\qquad \text {EFFECT: } \neg \operatorname{At}(\text {obj, } \text {loc}) \wedge \text
{At}(\text {obj, Ground}) \text {) }
Action ( Remove ( obj, loc ) , PRECOND: At ( obj , loc ) EFFECT: ¬ At ( obj, loc ) ∧ At ( obj, Ground ) )
Putting Tire on
Action ( PutOn ( t , Axle ) , PRECOND: Tire ( t ) ∧ A t ( t , Ground ) ∧ ¬ At ( Flat , Axle ) EFFECT: ¬ A t ( t , Ground ) ∧ A t ( t , Axle ) )
\text {Action }(\operatorname{PutOn}(t, \text { Axle}), \\\qquad \text {PRECOND: Tire}(t) \wedge A t(t,
\text {Ground}) \wedge \neg \operatorname{At}(\text {Flat}, \text {Axle}) \\\qquad \text {EFFECT: } \neg A
t(t, \text { Ground }) \wedge A t(t, \text{Axle}))
Action ( PutOn ( t , Axle ) , PRECOND: Tire ( t ) ∧ A t ( t , Ground ) ∧ ¬ At ( Flat , Axle ) EFFECT: ¬ A t ( t , Ground ) ∧ A t ( t , Axle ))
Leaving tire overnight
Action ( LeaveOvernight) , PRECOND: EFFECT: ¬ At ( Spare, Ground ) ∧ ¬ A t ( Spare, Axle ) ∧ ¬ A t ( Spare, Trunk ) ∧ ¬ A t ( Flat, Ground ) ∧ ¬ A t ( Flat, Axle ) ∧ ¬ At(Flat, Trunk) )
\text { Action }(\text {LeaveOvernight)}, \\\qquad \text {PRECOND: } \\\qquad \text {EFFECT: } \neg
\operatorname{At}(\text {Spare, Ground}) \wedge \neg A t(\text {Spare, Axle}) \wedge \neg A t(\text {Spare,
Trunk}) \wedge \neg A t(\text {Flat, Ground}) \wedge \neg A t(\text {Flat, Axle}) \wedge \neg \text
{At(Flat, Trunk)})
Action ( LeaveOvernight) , PRECOND: EFFECT: ¬ At ( Spare, Ground ) ∧ ¬ A t ( Spare, Axle ) ∧ ¬ A t ( Spare, Trunk ) ∧ ¬ A t ( Flat, Ground ) ∧ ¬ A t ( Flat, Axle ) ∧ ¬ At(Flat, Trunk) )
The following plan is a solution to the problem:
[ Remove ( Flat, Axle ) , Remove ( Spare, Trunk ) , PutOn(Spare, Axle) ]
[\text {Remove}(\text {Flat, Axle}), \text {Remove}(\text {Spare, Trunk}),\text {PutOn(Spare, Axle)}]
[ Remove ( Flat, Axle ) , Remove ( Spare, Trunk ) , PutOn(Spare, Axle) ]
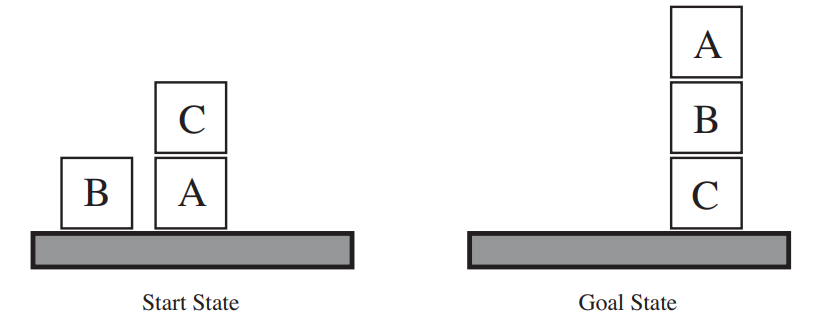
Example: Blocks World This domain consists of a set of cube-shaped blocks sitting on a table.
The arm can pick up only one block at a time, so it cannot pick up a block that has another one on it.
Initial value and goal state
Init ( On ( A , Table ) ∧ On ( B , Table ) ∧ On ( C , A ) ∧ B l o c k ( A ) ∧ B l o c k ( B ) ∧ B l o c k ( C ) ∧ C l e a r ( B ) ∧ C l e a r ( C ) )
\operatorname{Init}(\text {On}(A, \text {Table}) \wedge \operatorname{On}(B, \text {Table}) \wedge
\operatorname{On}(C, A) \wedge Block(A) \wedge Block(B) \wedge Block(C) \wedge Clear(B) \wedge Clear(C))
Init ( On ( A , Table ) ∧ On ( B , Table ) ∧ On ( C , A ) ∧ Bl oc k ( A ) ∧ Bl oc k ( B ) ∧ Bl oc k ( C ) ∧ Cl e a r ( B ) ∧ Cl e a r ( C ))
Goal ( On ( A , B ) , On ( B , C ) ) \text{Goal}(\text{On}(A,B), \text{On}(B,C)) Goal ( On ( A , B ) , On ( B , C ))
Actions:
Action ( Move ( b , x , y ) , PRECOND: On ( b , x ) ∧ Clear ( b ) ∧ Clear ( y ) ∧ Block ( b ) ∧ Block ( y ) ∧ ( b ≠ x ) ∧ ( b ≠ y ) ∧ ( x ≠ y ) EFFECT: On ( b , y ) ∧ Clear ( x ) ∧ ¬ On ( b , x ) ∧ ¬ Clear ( y ) )
\operatorname{Action}(\operatorname{Move}(b, x, y), \\\qquad \text {PRECOND: } \text{On}(b, x) \wedge \text
{Clear}(b) \wedge \operatorname{Clear}(y) \wedge \text {Block}(b) \wedge \operatorname{Block}(y) \\\qquad
\wedge (b \neq x) \wedge(b \neq y) \wedge(x \neq y) \\\qquad \text {EFFECT: } \operatorname{On}(b, y) \wedge
\operatorname{Clear}(x) \wedge \neg \text{On}(b, x) \wedge \neg \operatorname{Clear}(y))
Action ( Move ( b , x , y ) , PRECOND: On ( b , x ) ∧ Clear ( b ) ∧ Clear ( y ) ∧ Block ( b ) ∧ Block ( y ) ∧ ( b = x ) ∧ ( b = y ) ∧ ( x = y ) EFFECT: On ( b , y ) ∧ Clear ( x ) ∧ ¬ On ( b , x ) ∧ ¬ Clear ( y ))
Action ( MoveToTable ( b , x ) , PRECOND: On ( b , x ) ∧ Clear ( b ) ∧ Block ( b ) ∧ ( b ≠ x ) EFFECT: On ( b , Table ) ∧ Clear ( x ) ∧ ¬ On ( b , x ) )
\text {Action}(\text {MoveToTable}(b, x), \\\qquad \text {PRECOND:} \operatorname{On}(b, x) \wedge
\text{Clear}(b) \wedge \operatorname{Block}(b) \wedge(b \neq x) \\\qquad \text {EFFECT:} \text{ On}(b, \text
{Table}) \wedge \operatorname{Clear}(x) \wedge \neg \text{On}(b, x))
Action ( MoveToTable ( b , x ) , PRECOND: On ( b , x ) ∧ Clear ( b ) ∧ Block ( b ) ∧ ( b = x ) EFFECT: On ( b , Table ) ∧ Clear ( x ) ∧ ¬ On ( b , x ))
The following plan is a solution to the problem:
[ MoveToTable ( C , A ) , Move ( B , Table, C ) , Move ( A , Table , B ) ]
[\text {MoveToTable}(C, A), \text {Move}(B, \text {Table,} C), \text {Move}(A, \text {Table}, B)]
[ MoveToTable ( C , A ) , Move ( B , Table, C ) , Move ( A , Table , B )]