Game show host gives you a coin
EMV
EMV=21($0)+21($2,500,000)=$1,250,000
Expected utilities
Lets say
Sn
is the state of owning
n
dollars.
Our current financial status is
Sk
.
EU( Accept )EU( Decline )=21U(S
k
)+21U(S
k
+2,500,000)=U(S
k
+1,000,000)
The Utility for getting your first million dollars is very high, but the utility for the additional million is smaller.
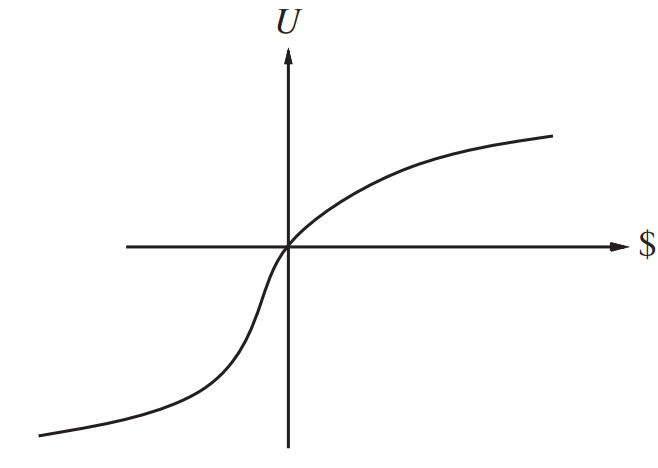 exactly proportional to the logarithm
exactly proportional to the logarithmLets say
U(Sk)=5
U(Sk+1,000,000)=8
U(Sk+2,500,000)=9
Then the rational agent (that is not a billionaire) would decline although the EMV is higher.
EU( Accept )EU( Decline )=21⋅5+21⋅9=7=8
A billionare would have a locally linear utility function and accept.
Conclusion:
In general we can say that
in the positive part of the curve
where the slope is decreasing, for any lottery
L
:
U(L)<U(S
EM
V
(L))
the utility of being faced with that lottery
<
than the utility of being handed the expected monetary value of the lottery with absolute certainty
