Vorgang:
-
Zustände? →
Q
und
I,F
- Aktionen/Eingaben? → die Zustandsübergänge auslösen / dabei stattfinden
- Tabelle erstellen, alle Fälle abdecken
Beispiel: Simpsons Flussbeispiel
Dieses Beispiel wäre als Automat leichter zu modellieren.
MKGH… Maggie … Knecht Ruprecht … Gift … Homer ⎭⎬⎫
System Koponenten
System-Zustand:
Dinge hierDinge dort\frac{\text{Dinge hier}}{\text{Dinge dort}}Dinge dortDinge hierEndzustand:-MKGHAnfangszustand:MKGH-\textsf{Endzustand: }\frac{\text{-}}{\text{MKGH}} \qquad \textsf{Anfangszustand: }\frac{\text{MKGH}}{\text{-}}Endzustand:MKGH-Anfangszustand:-MKGHVerbotene Zustände:
GHMK,MKGH,KHMG,MGKH,HMKG,MKGH\frac{G H}{M K}, \frac{M K}{G H}, \frac{K H}{M G}, \frac{M G}{K H}, \frac{H}{M K G}, \frac{M K G}{H}MKGH,GHMK,MGKH,KHMG,MKGH,HMKG
Zustandsübergänge:
h,m,k,g
Dadurch Automat ohne verbotenen Zuständen:
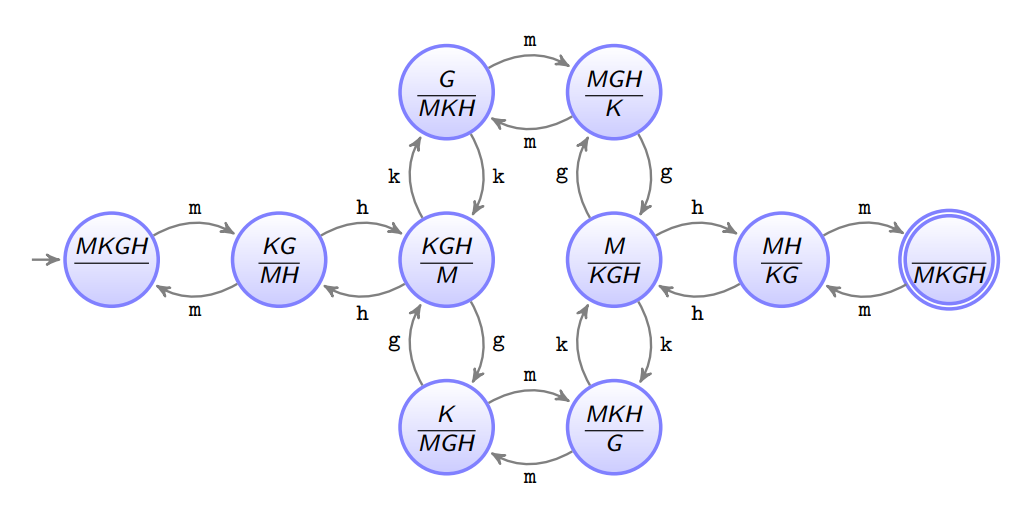
Alle gültigen Wörter (die zum Ziel führen) sind die Sprache des Automaten.
Mögliche Lösungen:
{ mhkmghm, mmmhhhgmkhm, ..., mhkmgkmgkmghm, ... }
Beispiel: RLL (run-length limited) Codes
Daten werden auf Festplatten, CDs und DVDs binär kodiert.
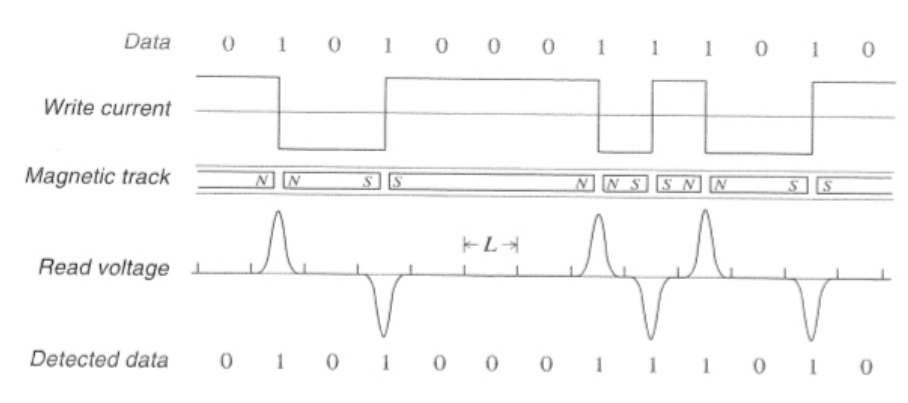
Probleme: Abstand zwischen den 1en...
- zu groß - zu viele 0en - Synchronisation geht verloren
- zu klein - zu wenige 0en - ununterscheidbar
(m : n)-(d, k)-RLL-Codes
Wir wollen die Anzahl der 0en beeinflussen.
Ziel: minimiere n/m, maximiere d
Lösung: Nütze die „natürlichen“ 0er-Strecken und 1er im Datenstrom.
m Datenbits→n Codebits
Zwischen zwei 1 sollen:
min d, max k
0 vorkommen.
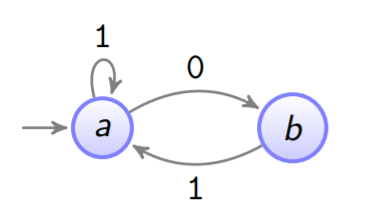
(1 : 2)-(0, 1)-RLL-Code
1 eingabe-bit → 2 ausgabe-bits
Es dürfen nicht zwei 0 hintereinander vorkommen.
Wir machen einen Automaten der das erzwingt. (Ausgaben)
-
Zustand
a
hat 2 augehende Kanten.
-
Zustand
b
hat 1 augehende Kante. → problematisch bei 3 input bits
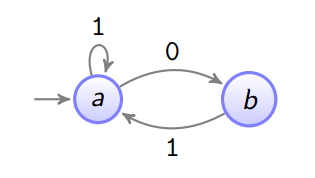
Wir "Potenzieren" den Automaten (mehr Kanten)
-
Zustand
a
hat 3 augehende Kanten.
-
Zustand
b
hat 2 augehende Kanten.
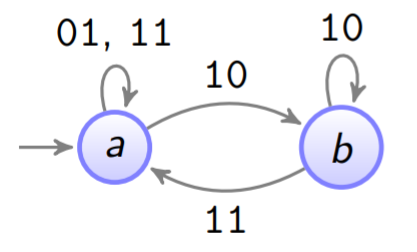
Jetzt entscheidet man willkürlich welches der 3 Kanten man für
0
und welches man für
1
wählt:
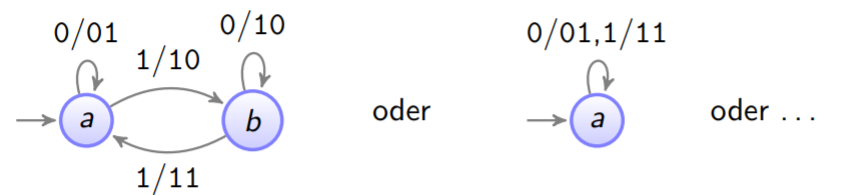
10010⇒10 10 10 11 01 oder 11 01 01 11 01 oder...
Bedingung bleibt immer erhalten.
Vorherige Beispiele
(1:2)-(0,1)-RLL Encoder
A=⟨{a,b},{0,1},{01,10,11},δ,γ,a⟩
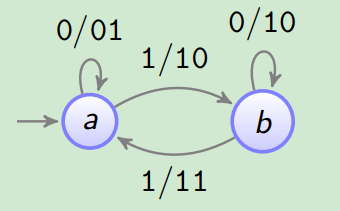
δ
ab0ab1ba
Zustand
γ
ab0011011011
Ausgabe
w
:[A](
w
):εε001110000101101010010110111011000010101100101010⋯⋯
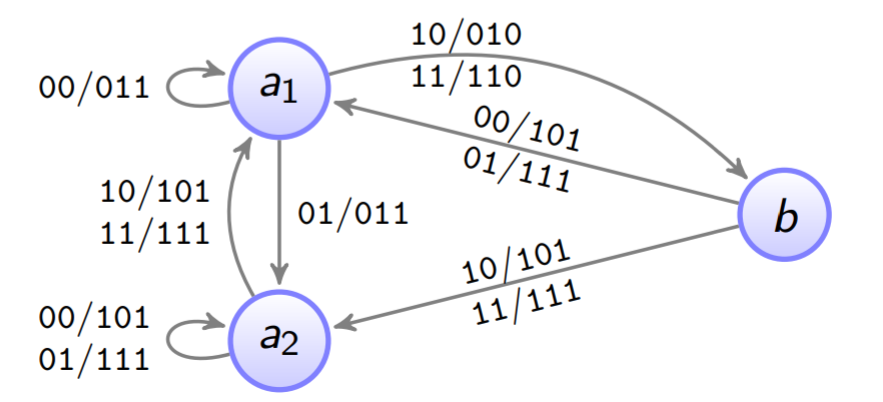
(1:2)-(0,1)-RLL Encoder
A=⟨{a,b},{0,1},{01,10,11},δ,γ,a⟩bei Mealy
A=⟨{a1,a2,b},{0,1},{01,10,11},δ,γ,a⟩
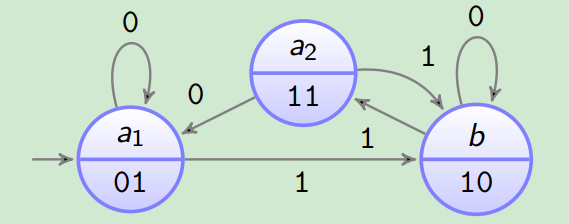
δ
a
1
a
2
b0a
1
a
1
b1bba
2
γ
a
1
a
2
b011110
(2 : 3)-(0, 1)-RLL-Code
2 eingabe-bits → 3 ausgabe-bits
Es dürfen nicht zwei 0 hintereinander vorkommen.
Wir machen einen Automaten der das erzwingt. (Ausgaben)
-
Zustand
a
hat 2 augehende Kanten. → problematisch bei 4 input bots
-
Zustand
b
hat 1 augehende Kante. → problematisch bei 4 input bits
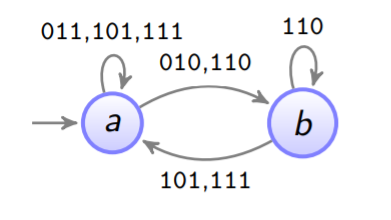
Wir "Potenzieren" den Automaten mehrmals (mehr Kanten)
-
Zustand
a
hat 2 augehende Kanten. → immer noch problematisch
-
Zustand
b
hat 2 augehende Kanten. → immer noch problematisch

Wir "splitten" Zustand
a
auf damit
b
mehr Kanten hat
-
Zustand
a1
hat 3 augehende Kanten.
-
Zustand
a2
hat 2 augehende Kanten.
-
Zustand
b
hat 3 augehende Kanten.
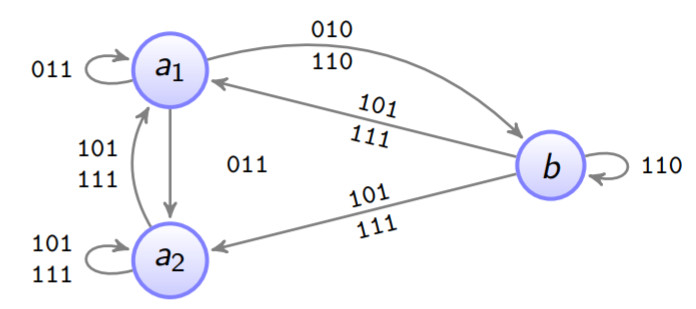
Mealy Automat: