Kontextfreie Grammatiken

Motivation

Nicht reguläre Sprachen lassen sich nicht durch reguläre Ausdrücke ausdrücken.

Beispiele: Wohlgeformte Klammerausdrücke:

$\{(),(()),()(),((())),(())(),()()(), \ldots\}$

$\left\{\mathrm{a}^{n} \mathrm{~b}^{n} \mid n \geq 0\right\}=\{\varepsilon, \mathrm{ab}, \text { aabb, aabbb }, \ldots\}$

Formale Sprache ist kontextfrei, wenn sie von kontextfreier Grammatik generiert werden kann.

Reguläre Sprache lässt sich durch kontextfreie Sprache ausdrücken aber nicht umgekehrt.

Dinge die nicht ausgedrückt werden können:

Formale Sprachen

$\left\{a^{n} b^{n} c^{n} \mid n \geq 0\right\}=\{\varepsilon, \text{abc}, \text{aabbcc}, \text { aaabbbccc }, \ldots\}$ ist nicht kontextfrei

$\left\{w w \mid w \in\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}^{*}\right\}$ ist nicht kontextfrei

Natürliche Sprachen

Kontext-Sensitive Sätze, Reime in natürlicher Sprache

Kontextfreie Grammatik

$G=\langle V, T, P, S\rangle$

$V$ Non-Terminale (Variablen)

$T$ Terminal-Symbole

$P \subseteq V \times (V \cup T)^*$ Produktionen

Man schreibt $A \rarr w$ statt $(A,w) \in P$

$S \in V$ Startsymbol

Ableitbarkeit $\Rarr$

Die Ableitungsregel beeinflusst nicht das Resultat.

Allgemein

Angenommen $x,y \in (V \cup T)^*$ :

$x Ay \Rarr xwy$ falls $A\rarr w \in P$

$u \stackrel{*}{\Rightarrow} v$ falls

$u=v$ oder

$u \Rightarrow u^{\prime} \wedge u^{\prime} \stackrel{*}{\Rightarrow} v$ für ein $u^{\prime} \in(V \cup T)^{*}$

Links-Ableitbarkeit

Variable ganz links zuerst ersetzt.

$x A y \Rightarrow_{L} x w y$ wenn $A \rightarrow w \in P, x \in T^{*}$

Rechts-Ableitbarkeit

Variable ganz rechts zuerst ersetzt.

$x A y \Rightarrow_{R} x w y$ wenn $A \rightarrow w \in P, y \in T^{*}$

Parallel-Ableitbarkeit

$x_{0} A_{1} x_{1} \cdots A_{n} x_{n} \Rightarrow_{P} x_{0} w_{1} x_{1} \cdots w_{n} x_{n}$

wenn $A_{1} \rightarrow w_{1}, \ldots, A_{n} \rightarrow w_{n} \in P$

und $x_{0}, \ldots, x_{n} \in T^{*}$

Kontextfreie Sprache $\mathcal L(G)$

Von Grammatik $G$ generierte Sprache

Quasi Menge aller mit der Grammatik ableitbaren Wörter.

$\mathcal{L}(G)=\{w \in T^{*} \mid S \stackrel{*}{\Rightarrow} w\}$

Alle Wörter aus Terminal-Verknüpfungen bei denen ein Startsymbol nach Ableitung zu einem gültigen Wort führt.

Beispiel:

$G=\langle\{S\},\{\mathrm{a}, \mathrm{b}\},\{S \rightarrow \varepsilon \mid \mathrm{a} S \mathrm{b}\}, S\rangle$

$\mathcal{L}(G)=\left\{\mathrm{a}^{n} \mathrm{~b}^{n} \mid n \geq 0\right\}=\{\varepsilon, \text { ab, aabb, aaabbb, } \ldots\}$

zB $S \stackrel{*}{\Rightarrow} \text {aabb}$ möglich weil

$S \Rightarrow \mathrm{a} S \mathrm{~b} \Rightarrow \mathrm{aa} S \mathrm{bb} \Rightarrow \mathrm{aa} \varepsilon \mathrm{bb}=\mathrm{aabb}$

1) Backus-Naur-Form BNF

$V$ in Spitzen klammern $\lang ~\dots ~\rang$

$T$ unter Anführungszeichen $\text{``..."}$

$::=$ Für Zuweisungen

Reele Numerale

$\langle\text { Real }\rangle:=\langle\text { Digit }\rangle\langle\text { Digits }\rangle \text { ``." }\langle\text { Digits }\rangle\langle\text { Scale }\rangle$

$\langle\text { Digit }\rangle:=\text { ``0" }|\dots| \text { ``9" }$

$\langle\text { Digits }\rangle::=\varepsilon \mid\langle\text { Digit }\rangle\langle\text { Digits }\rangle$

$\langle\text { Scale }\rangle::=\varepsilon \mid \text { ``E" }\langle\text { Sign }\rangle\langle\text { Digit }\rangle\langle\text { Digits }\rangle$

$\langle\operatorname{Sign}\rangle::=\left.\varepsilon~\right| \text { ``+" | ``-"}$

2) Erweiterte Backus-Naur-Form EBNF

Vorteile der BNF:

Keine Angabe von Terminalen und Nonterminalen sowie Anfangsterminalen mehr notwendig weil es sich von der Notation selbst ablesen lässt.

Man gibt nur noch die Produktionen an.

Vorteile derEBNF(verglichen zur BNF):

Leichtere Syntax ohne (<, >, ::=) indem zwischen Terminalen und Nonterminalen mit "" differenziert wird.

Abkürzungen aus regulären Ausdrücken übernommen wie (), [], {}, ? .

Regular Right Part Grammar (RRPG)

Man benutzt nur "" und die folgenden Klammern: Vermeidung von Rekursionen und Leerwörtern

$\left(w_i\right)$ 1 Mal $w_i$

$\left\{w_i\right\}$ ≥0 Mal $w_i$

$\left[w_i\right]$ 0-1 Mal $w_i$

3) (Rekursive) Syntaxdiagramme

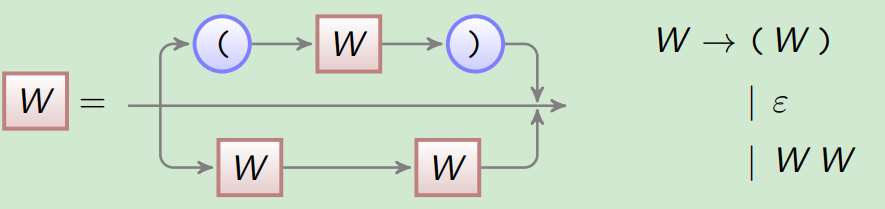
Beispiele

Syntax aussagenlogischer Formeln

$G=\langle\{F m, O p, \operatorname{Var}\}, T, P, F m\rangle$

$T=\{\top, \perp, \neg,(,), \wedge, \uparrow, \vee, \downarrow, \equiv, \not \equiv, \supset, \subset\} \cup \mathcal{V}$

$\begin{aligned}P=\{& F m \rightarrow \operatorname{Var}|\top| \perp|\neg F m|(F m O p F m), \\& O p \rightarrow \wedge|\uparrow| \vee|\downarrow| \equiv|\not \equiv| \supset \mid \subset \\& \operatorname{Var} \rightarrow \mathrm{A}|\mathrm{B}| \mathrm{C} \mid \cdots\}\end{aligned}$

Beispiel: $((A \uparrow B) \uparrow(A \uparrow B))$

$\begin{aligned}F m & \Rightarrow_P P(F m O p F m) \\& \Rightarrow_P P((F m O p F m) \uparrow(F m O p F m)) \\& \Rightarrow_P P((\operatorname{Var} \uparrow \operatorname{Var}) \uparrow(\operatorname{Var} \uparrow V a r)) \\& \Rightarrow_P P((A \uparrow B) \uparrow(A \uparrow B))\end{aligned}$

Reele Numerale

$G=\langle V, T, P, \text { Real }\rangle$

$V=\{\text { Real, Scale, Sign, Digits, Digit }\}$

$T=\{0, \ldots, 9, ., \mathrm{E},+,-\}$

$P =\{\\ \quad Real \rightarrow Digit ~ Digits . Digits ~ Scale \\ \quad Scale \rightarrow \varepsilon \mid E ~ Sign ~ Digit ~Digits \\\quad \operatorname{Sign} \rightarrow \varepsilon|+|- \\\quad Digits \rightarrow \varepsilon \mid Digit ~Digits \\\quad Digit \rightarrow 0|\cdots| 9 \\ \}$

Wohlgeformte Klammerausdrücke

Sie sind die Stärke der kontextfreien Grammatik die sie vor allem von regulären Sprachen unterscheidet.

$G=\langle\{W\}, \quad\{(,)\}, \quad\{W \rightarrow \varepsilon|(W)| W W\}, \quad W\rangle$

$\mathcal{L}(G)=\{\varepsilon,(),(()),()(),((())),(())(),()(()),()()(), \ldots\}$