Information flow determines Information security.

(End-to-end) Confidentiality no leakage, no insecure information flow

Integrity data only changed when authorized

Until now we used different security mechanisms.

Problem of security mechanisms:

Solution: language-based approach

Side channels

Mechanisms to get sensitive information through the observable behaviour of a computing system.

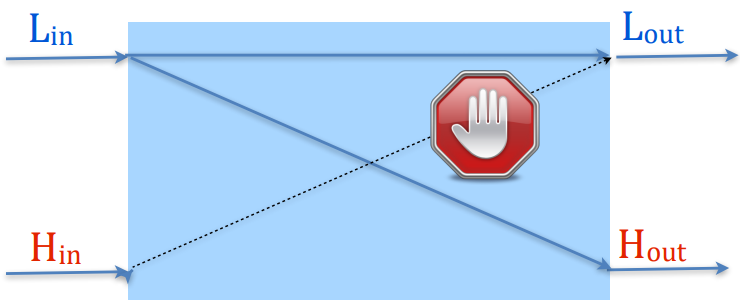
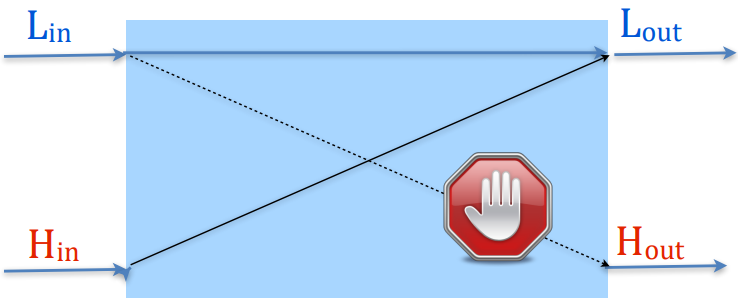
Explicit flow information leakage through direct assignment.

Implicit flow control structure of the program. (Using $H$ as a guard)

Termination channels termination / non-termination.

Timing channels execution time of program, cache access time, $\dots$

Probabilistic channels different stochastic properties, observing behaviour of execution scheduler

Power channels Power consumption by computer

Resource exhaustion c. exhaustion of a finite, shared resource: memory space, $\dots$

Confidentiality, Integrity

Informal definition of Non-Interference

Non interference = formal definition of confidentiality.

Program is secure if high inputs do not interfere with low inputs.

Computation $\text{C}$ , with semantics $\llbracket \mathrm{C} \rrbracket$ (maps the input to the output or does not terminate $\bot$ )

where

Confidentiality vs. Integrity are dual

Security Types, Security Lattice

Multiple security types: One for confidentiality, one for integrity

High confidentiality means low integrity - vice versa.

$\ell=L_{1} L_{2}$ confidentiality level $\cdot$ integrity level

Formal definition of non-interference

Program $\text{c}$ satisfies non-interference, if:

where$(\mu \sim_\ell v)$means that$\mu$and$v$are equivalent at level$\ell$or lower.

This definition is incomplete:

Considering Termination

If they do terminate, then they must have the same lower part.

Security Type System

non-interference definition contains a universal quantification over all possible inputs → undecidable.

Static analysis

We type expressions and then enforce rules.

Good option but incomplete because of undecidability.

Insecure program might get accepted.

• Description of used notation

  We write the preconditions for above the line: $\frac{\textsf{precondition}}{\textsf{assignment}}$

  $\ell=H \mid L$(Security) Types

  $L \sqsubseteq H$Simple lattice (there could theoretically be more Types between$L$and$H$)

  $\Gamma=x_{1}: \ell_{1},~ \ldots,~ x_{n}: \ell_{n}$Function that assigns types to variables ("typing environment")

  $p c:=\ell$Program counter (as security type)

  $\Gamma \vdash e$Judgement: expression$e$is well typed in$\Gamma$

  $\Gamma, p c \vdash c$Judgement: program$c$is well typed in$\Gamma$and$pc$

  $\sqcup$("join") - like Max function for upper bounds

Assigned type

Type $\ell$ of $x$ as assigned by $\Gamma$

program counter$pc$

always has the higher type: $\ell \sqcup p c = \max(\ell, p c )$

Explicit flow, impicit flow

If expression $e$ has type $\ell$ then:

$\ell \sqcup p c$ must be lower than the type of $x$ . (implicit flow through$pc$and explicit flow through$\Gamma(x)$)

Number$n$— skip instruction — sequencing instructions

Declassification

Sometimes necessary to allow explicit flow ie. for checking passwords. We do not check $\ell \sqcup p c \sqsubseteq \Gamma(x)$ anymore.

Considering Timing: hiding timing leaks

Cross-copy low slices = dummy instructions (like skip sequences) in each branch that so that both take an equal amount of time - means number of instructions per branch must be equal.

The guard must be low and the entire instruction must be checked under a low $pc$ . We don't want different looping times based on the guard.