Bitonic merge

Bitonic merge / Even-odd merge (optional)

Drawback of merge with rank-based algorithms:

reading elements at the same time (not allowed in EREW PRAMs).

Inefficient when only $\small O(p)$ elements must be merged on $\small p$ processors.

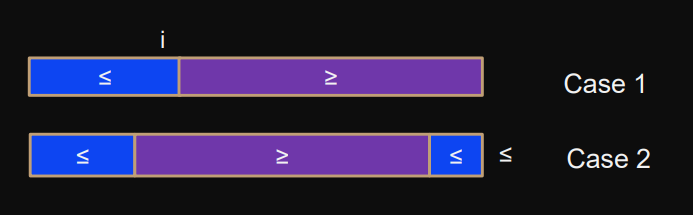
Bitonic sequence (Definition)

Sequence $\small (a_0, a_1, \dots ,a_{n-1})$ is bitonic if

either there is an index $\small i$ such that

$\small a_0 \leq a_1 \leq \dots \leq a_i$

$\small a_{i+1} \geq a_{i+2} \geq \dots \geq a_{n-1}$

or there is a cyclic shift such that the first case holds (first case holds if we just shift all elements to left or right)

Lemma

Let $\small a = (a_0, a_1, \dots ,a_{n-1})$ be a bitonic sequence with even length $\small n$ .

If $\small n$ is odd we can put the real $\small a_{n-1}$ in either $\small a'$ or shifted $\small a''$ → the algorithm is then not oblivious anymore.

Let $\small a', a''$ be two sequences of length $\small n/2$ :

$\footnotesize a' = (\min(a_0, a_{n/2}),~\min(a_1, a_{n/2+1}),~\dots,~\min(a_n, a_{n-1}))$

$\footnotesize a'' = (\max(a_0, a_{n/2}),~\max(a_1, a_{n/2+1}),~\dots,~\max(a_n, a_{n-1}))$

This makes $\small a', a''$

bitonic

$\small a' \leq a''$ for all elements they contain

Proof of lemma
1. Any subsequence of a bitonic sequence is also bitonic.
  $\small a', a''$ are also (disjoint) subsequences of $\small a$ .
  Concatinating them makes $\small a$ .
1. Contradiction: Assume that there is some $\small a'_i > a''_j$
  $\small a'_i = \min (a_i,~a_{i+n/2}) = a_i$
  then $\small a'_i = a_i> a''_j$
  This contradicts that either $\small a'_i$ is $\small \min$ or $\small a''_j$ is $\small \max$ .

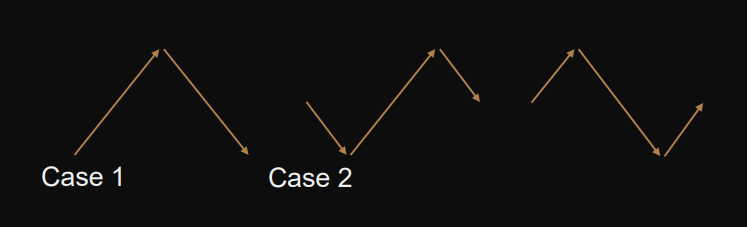
Examples

visualization

$\small n = 6$

a = a_0,   a_1,   a_2,   a_3,   a_4,   a_5
↓      ↓      ↓      ↓      ↓      ↓
0      1      2     n/2   n/2+1  n/2+2     indices
|____________________|
|____________________|              comparisions
|____________________|

Example 1
$\small a = (1,1,2,3,4,7,7,6,5,4,4,3) = (1,1,2,3,4,7)~||~(7,6,5,4,4,3)$
$\small a' = (1,1,2,3,4,3)$
$\small a'' = (7,6,5,4,4,7)$

Example 2 (cyclically shifted)
$\small a = (3,4,7,7,6,5,4,4,3,1,1,2) = (3,4,7,7,6,5)~||~(4,4,3,1,1,2)$
$\small a' = (3,4,3,1,1,2)$
$\small a'' = (4,4,7,7,6,5)$

Ordering bitonic sequences

= oblivious merge

bitonic_merge(int a[], int n) {
if (n==1) {
return;
}// n is odd
int nn = n/2;                 // offset
int s = n/2;	                // size of (first half) a'if (n%2 == 1) {
nn++;
if (a[n/2] < a[n-1]) {      // a[n/2] will be in a' and a[n-1] in a''
s++;
}
}for (i=0; i<n/2; i++) {       // parallelizable
int mina, maxa;
mina = min(a[i], a[i+nn]);
maxa = max(a[i], a[i+nn]);
a[i] = mina;                // (first half) a'
a[i+nn] = maxa;             // (second half) a''
}
// recursive call of each half
bitonic_merge(a,s);
bitonic_merge(a+s,n-s);
}

Given sequence $\small a$ split into $\small a', a''$ with the definition given above.

Then recursively order $\small a', a''$ .

Hint: Our pseudocode is written in C.

Therefore in the last instruction bitonic_merge(a+s, s-n); we are passing the start index of the array +s and the length s-n .

Work

$\small \text{Wpar}(1) \in O(1)$

$\small \text{Wpar}(n) \in O(n) + 2\cdot \text{Wpar}(n/2) = O(n \log n)$

$\small \text{Wpar}(n) = n + 2\cdot (n/2 \cdot \log_2(n/2)) = n+ n \log_2(n/2) = n + n \log_2 n - n = n \log_2 n$

$\color{pink}\small \text{Wpar}(n) = n \log_2 n$

Theorem

On a shared-memory system a bitonic sequence of length $\small n$ can be sorted in

$\small \lceil \log_2n\rceil$ parallel steps

$\small O(n \log n)$ operations

time of $\small O((n \log n) / p + \log p)$

space of $\small O(n)$ (this means it can be done in place)

The sorting is not stable.

When $\small n> p$

call bitonic_merge() recursively until

$\small n/2^k = n/p \quad \Longleftrightarrow \quad k = \log_2p$

Then merge subsequences of length $\small n/p$ sequentially on the $\small p$ processors.

Work per execution step is $\small O(n)$ , therefore total work is $\small O(n \log p)$ .

$\color{pink}\small \text{Wpar}(n) = O(n \log p)$

Not work optimal.

Output is bitonic but $\small n+m$ may not be a power of two.

Add padding in the beginning out output (value: $\small -\infin$ ) as a virtual element.

Comparator Networks

Comparator networks as a model for parallel sorting

Comparator min/max operation

Depth longest path from input to output

Size number of comparators/operations

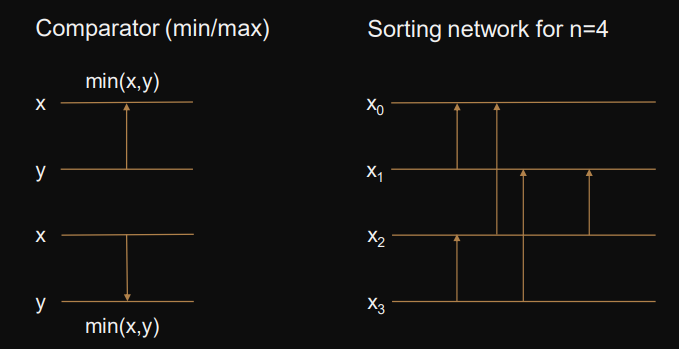
Example: Bather’s bitonic sorting network

Depth $\small O(\log (n)^2)$

Size $\small O(n \cdot \log (n)^2)$

Question: What is the minimal depth and size for sorting $\small n$ numbers with a sorting network

Question remains unsolved.

Depth $\small O(\log n)$ and size $\small O(n \log n)$ ? → No.

Size $\small O(n \log n)$ ? → Possible with AKS network but not practical.

$\small O((n \log n) / p + \log n)$ → Possible with EREW PRAM mergesort but not practical.