Distributed Systems

Models

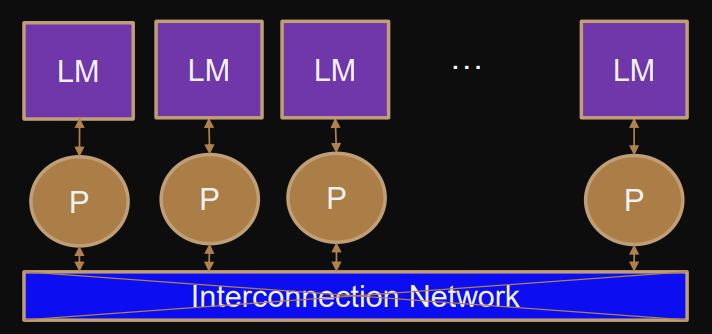
Naive distributed memory system - architecture

Distributed memory PRAM:

Single processors.

Communication / interconnection network → Network properties determine communication performance.

Local and distributed memory.

Naive distributed memory system - parallel programming model

Independent, non synchronized processes executed by processors .

Locally stored program on local data.

Interaction with other processes exclusively via explicit communication.

Models:

Communication driven (in this course)
explicit message passing between processors (pairs or groups).
ie. MPI, PVM, Occam, ...

Data distribution driven
Partitioned Global Address Space (PGAS) and data structures over preocessors.
implicit communication through data access.
ie. UPS, Titanium, Chapel, X10, Global Arrays, HPF

Cost model

Communication (needs its own cost model: cost model for network communication)

Local vs. non-local memory access

Local memory hierarchy (caches)

Network properties

Structure Network topology

Capabilities Possible operations per network component

Routing techniques

Switching strategy

Cost Latency, Bandwidth

Network latency

Time until first data element arrives from source to destination processor.

Network bandwidth

How many data elements can be transferered from source to destination processor per time unit (GBytes / second)

k-ported

1-ported commun. system processor can send/receive to max 1 other processor

k-ported commun. system processor can send/receive to max k other processors

Direction

Uni-directional processor can send xor receive in each communication step

Bi-directional processor can send and receive in each communication step

from/to the same sender/recipient (telephone model)

from/to different senders/recipients (send-receive model)

Graph

Topology

Modeled as directed or undirected graph $\small G=(V,E)$ .

Nodes $\small V$ network elements: processors, network switches, ...

Edges $\small E$ uni or bi-directed link: cable, optical connection, ...

path(u,v)

path from node $\small u$ to $\small v$ : length of shortest path.

Shortest path between two nodes = lower bound for their latency.

diameter(G)

Max length of shortest path in graph.

$\small \text{diameter}(G) = \forall u,v\in V: \max (|\text{shortest path}(u,v)|)$

Diameter of graph = lower bound for number of rounds for collective communication operations.

degree(G)

Max number of edges of any node in graph.

$\small \text{degree}(G) = \forall v\in V: \max (\text{edges}(v))$

Degree of graph = “cost factor”, potential for more simultaneous communication (multi-port)

bisection-width(G)

Min number of edges to remove to partition graph into two roughly equal-sized, disconnected parts.

$\small \text{bisection-width(G)} = \min(|\{~(u,v) \in E ~|~u \in V_1,~ v\in V_2~\}|)$

where $\small |V_1| = |V_2|$ .

NP-hard problem (graph partitioning).

Bisection-width of graph = Lower bound for transpose operations (Each processor has to exchange information with every other one.)

Directed network

Only elements are processors (no switch nodes)

ie. mesh/torus, ring, hypercube, Kautz-network, ...

Indirected network

Processors connected via dedicated switch nodes

Fat tree, Clos network (InfiniBand), butterfly network, dragonfly network, ...

Broadcast

Broadcast problem (in communication network)

Collective operation.

One processor (root) wants to communicate data to all other processors.

Assumption: All other processors know which processor is root.

Broadcast problem model

All processors start at the same time - and are synched in rounds.

In each round $\small O(p/2)$ processors can communicate (limited by topology) .

Cost of each round:

= largest message sent.

= max number of messages sent/received over by each processor.

We want to determine the lower bound for the algorithm.

Recursive/binomial tree broadcast algorithm

if |V|=1 donePartition processors into two roughly equal-sized sets V1 and V2Assume root r1 in V1, choose a pseudo-root r2 in V2
Send data from r1 to r2
Recursively broadcast in V1 and V2

$\small\Omega( \lceil \log_2(p) \rceil)$ rounds are needed to solve this problem.

1-ported network

Rounds: $\small \Theta(\lceil \log_2(p) \rceil)$
Assume communication in synchronized rounds.
After data is sent from r1 to r2 , the two problems take half the original size and are solved independently.
Information theoretic argument:
In each round the number of processors that have data can at most double (by sending data to where data was not before).
Notice that: $\small \lceil \log_2(p) \rceil > \text{diameter}(G)$ , this is because we can only send data to one other node at a time.
This algorithm has the lowest number of possible rounds as its lower and upper boundary, therefore $\small \Theta$ .

k-ported network

Rounds: $\small \Theta(\lceil \log_{\textcolor{pink}{k+1}}(p) \rceil)$

same reason as above

Examples

Diameter of graph determines broadcast complexity.

Best case: fully connected network (optimal diameter)

Worst case: Linear array, ring, tree

Topologies

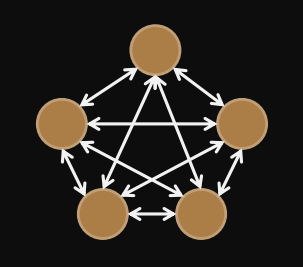
Fully connected network

All processors are directly connected to eachtother.

links = $\small p^2-p$

diameter = $\small 1$

bisection width = $\small (p/2)^2$

degree = $\small p-1$

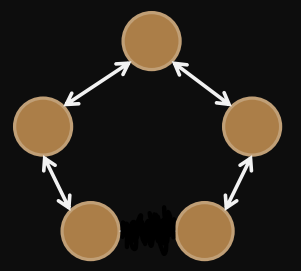
Linear array

diameter = $\small p-1$

bisection width = $\small 1$

removing one link disconnects network

degree = $\small 2$

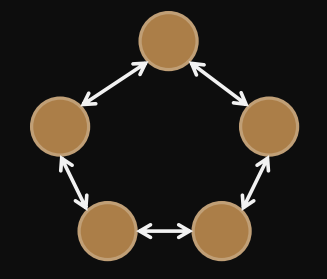
Ring

diameter = $\small p/2$

bisection width = $\small 2$

removing two links disconnects network

degree = $\small 2$

Tree

diameter = $\small 2 \cdot \log_2((p+1)/2)$

bisection width = $\small 1$

removing one link disconnects network

degree = $\small 3$

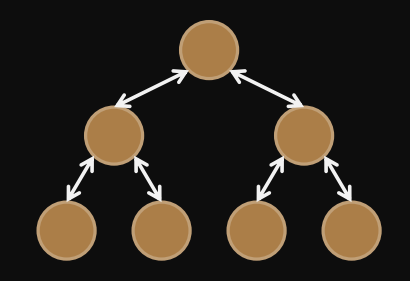
Mesh

diameter = $\small d \cdot (p-1)^{1/d}$

bisection width = $\small p^{(d-1)/d}$

bisection bandwidth determines transpose/alltoall complexity

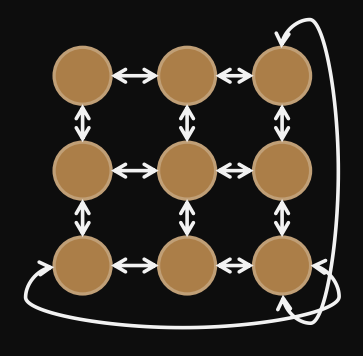
Torus (regular, 2D)

“wrap around”: nodes on the “edges” of 2D shape are all connected.

diameter = $\small d \cdot \lfloor (p/2)^{1/d}\rfloor$

bisection width = $\small 2\cdot p^{(d-1)/d}$

bisection bandwidth determines transpose/alltoall complexity

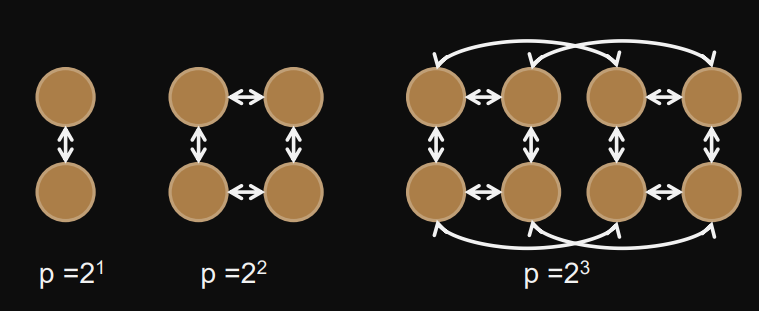
Hypercube

diameter = $\small d = \log_2 (p)$

bisection width = $\small p/2$

degree = $\small d = \log_2 (p)$

Routing terminology

Source (processor) wants to send message to destination (processor).

Routing protocol

We need an algorithm that finds a path (and considers traffic).

Correctness

Routing protocol must be deadlock free.

Sent messages must arrive (even with traffic).

Perfromance

Delays must be minimized.

Contention (”hot spots”) must be avoided.

Shared buffers (bound buffers) must be used.

Deterministic (oblivious) routing

Message path only determined by source, destination, static network properties.

Adaptive routing

Message path determined dynamically (ie. based on traffic)

Minimal routing algorithm

Route is shourtest path

(non minimal algorithm might choose longer paths ie. to avoid hot-spots)

Circuit switching

Entire path is reserved for the duration of the entire transmission

Packet switching

Message partitioned into smaller packets that can be transfered independently (they may not arrive in order)

Store-and-forward

Each node on path stores whole packet (message) before forwarding.

Transmission cost model

Cost of transmission over a single edge

Cost of transmitting data / communicating along a single edge $\small (u,v) \in E$ is linear in $\small m$ :

$\alpha + \beta \cdot m$

where:

$\small m$ size of transmitted data

$\small \alpha$ ”start-up” latency constant

$\small \beta$ time per unit (byte) constant

In this model:

both processors $\small u,v$ are involved during the whole transmission.

using recursive broadcast algorithm (see above) therefore:
time complexity: $\small T(m) = (\log_2(p)) \cdot \underbrace{(\alpha + \beta \cdot m)}_{\text{cost for single edge}}$

Pipelining

Fully connected network

lower bound $\small \Omega$ of broadcast in linear cost, fully connected network:

$\small T(m) = \textcolor{gray}\Omega\textcolor{gray}(~~\max(\alpha \cdot \log_2(p), ~~\alpha + \beta \cdot m)~~\textcolor{gray})$

where:

$\small \log_2(p)$ total communication rounds

$\small \alpha \cdot \log_2(p)$ start-up latency multiplied by total communication rounds

$\small\alpha + \beta \cdot m$ transfer cost for a single edge

Notice that it isn’t $\small \textcolor{gray}{\max(}(\log_2 p)(α+βm)\textcolor{gray}{, ~~\alpha + \beta \cdot m)}$ .

This is because $\small m$ does not have to be sent as one unit and algorithms can do “pipelining”.

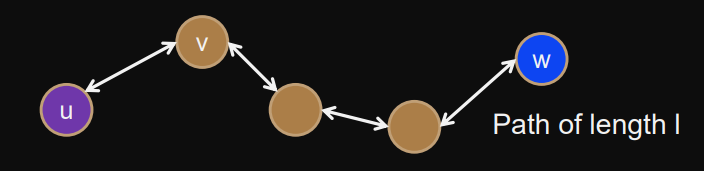
Store-and-forward routing

Transmission time via “store-and-forward”:

Each node on path stores whole packet (message) before forwarding.

Path of length $\small l$ :

$\small T(m) = l \cdot (\alpha + \beta \cdot m)$

Now when also pipelining with packet size $\small b$ :

$\small \lceil m / b \rceil$ = total num of packets

$\small T(m) = (l-1+m/b)α +(l-1)βb+βm$

We have to optimize for the best packet size.

Architectures

Hybrid / hierarchical parallel architectures

Processing elements organized hierarchically:

Nodes are not a single processor anymore but multi-processor systems with shared memory.

ie. traditional SMP clusters.

Alternatively: Multiple multi-processor systems as a single node.

Problem: Network bottleneck

Number of cores > number of ports

Sometimes when shared memory systems get complex, it can be reasonable to treat them as distributed systems.

Then programming must be done while keeping locality in mind.