Memory and Caching
Definition
Modern terminology
Core
CPU / Processing element PE (also still sometimes called processor)
Processor
several cores that can execute a program
- Multi-core processor
Processor with several cores physically on the same chip. Always shared-memory (typically caches).
- Many-core processor
Usually the GPU is meant.
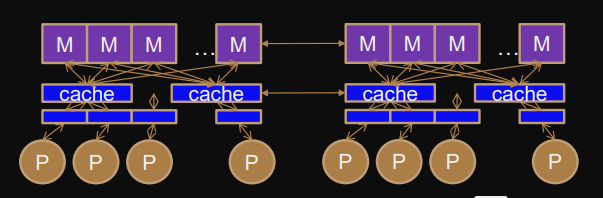
Multi-processor system
System with several processors, not necessarily on the same chip.
The processors can be multi-core and can have shared-memory or shared caches.
Programming model concepts
Thread, process program under execution
Task some piece of work to be executed by a process or thread
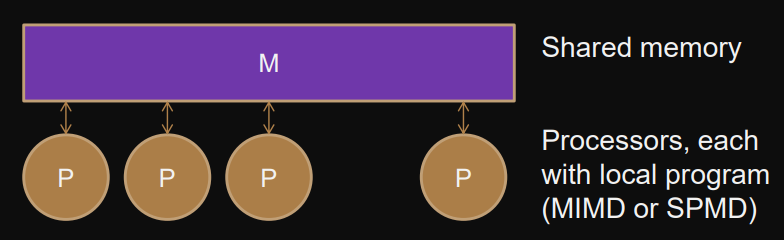
Shared-memory model
Shared memory models for architectures and machines
Naive shared memory model
Processors connected directly to memory (as in UMA or NUMA)
Read/write operations done independently (not PRAM, not lock-step, not synchronized)
Implicit assumption:
- Outcome is an interleaving of the instructions.
- Memory is consistent as defined by program order (read and write order).
Naive shared programming model
- Processors execute processes/threads inside each process.
Model does not specify which processor (core) executes it and there may be more threads than processors (oversubscription).
Symmetric multiprocessing SMP OS binds thread to core.
Improved performance by pinnning Explicitly binding thread to core.
ie. for utilization of private caches
Parallel computing (dedicated system) Num. of cores = threads and some pinning.
- Processes/threads are not synchronized.
- Processes/threads exchange data through shared memory.
- NUMA but entire memory is directly visible.
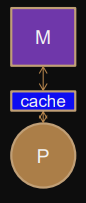
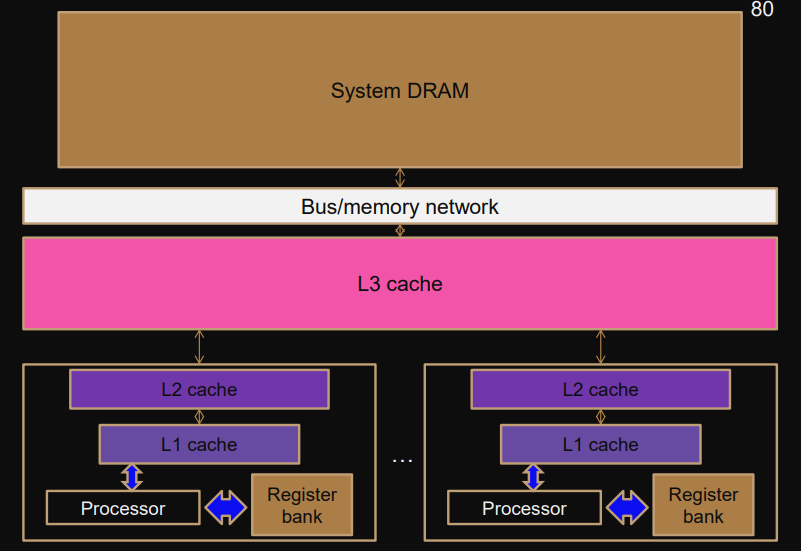
Cache
“Real” shared memory architecture
Cache (small and fast memory close to processor) and memory systems reduce memory bottleneck.
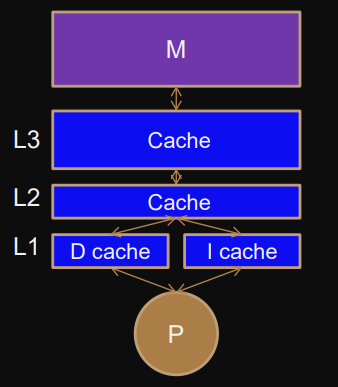
Modern processors use several different caches with different purposes and different levels.
Main memory GB space, >100 cycles per access
Cache Kb to MB space, 1-20 cycles per access
Register ≤64 bit, 0-1 cycles
Cache as a problematic abstraction (illusion)
In single processor architectures the cache contributes towards sustaining the RAM abstraction and is successful but in parallel processor architectures the abstraction becomes problematic:
Cache coherency problem synchronizing caches: local copy of one cache gets updated
Memory consistency problem different views in threads of what should be the same data
Cache Granularity
Cache consists of cache-lines/blocks of memory, used when reading/writing from main-memory.
Typical size: 64Bytes (8 doubles, 16 ints)
Locality
Caches make sense because of the following algorithm-properties:
temporal locality locations in memory used are used several times in succession
ie. when using the same operand (address)
spacial locality locations in memory used are close to eachother
ie. when using different indices of an array
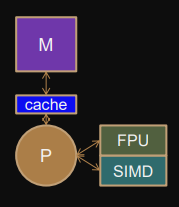
Multiprocessor/multi-core caches
Shared memory, cache coherent NUMA (ccNUMA) through memory network.
Several cores share caches at different levels.
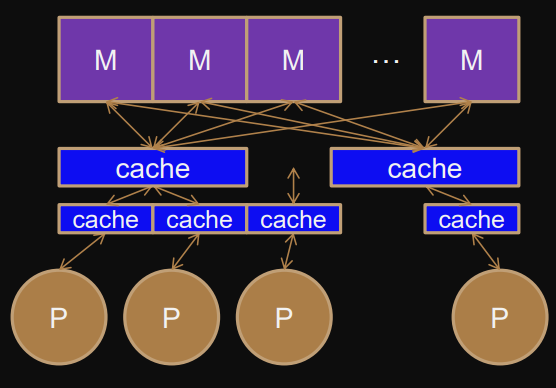
Mapping data from memory to cache
Assume data occupies as much space as a block or less.
- fully associative data can be stored in any cache-line
- set associative
data can be stored in a small set of cache-lines
in depth
Memory:
M[0, ..., n-1]Cache:
Lines [0, ..., m-1]where and block size .
k-way set associative means that the cache lines are grouped in
m/ksets — each set withkcache-lines.M[i]is cached in set(i/s) mod (m/k)Usually
m=2^rands=2^r'for somer,r'>0Mod and div then can be translated into mask and shift.
- directly mapped
data can be stored in only one specific cache-line
in depth
Memory:
M[0, ..., n-1]Cache:
Lines [0, ..., m-1]where and block size .
M[i]is cached in line(i/s) mod mM[0],…,M[s-1]go to line 0M[s],…,M[2s-1]to line 1…
M[m],…,M[m+s-1]again to line 0…
Usually
m=2^rands=2^r'for somer,r'>0Mod and div then can be translated into mask and shift.
Cache read/write-miss
A “cache-hit” is when the address is already in the cache and ready to be read.
Cache reading
Cache hit Read from cache
Read cache-miss Load block from memory into cache and read from cache
Cache writing
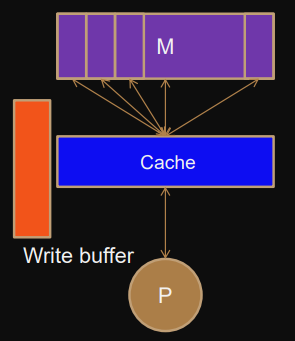
Cache hit Overwrite cache (and memory or wait until block is evicted)
a) Write-back cache
(typically also write-allocate)
block is passed to memory, when it’s being evicted from cache
b) Write-through cache
(typically also write-non-allocate)
each write to cache is immediately passed to memory
Write cache-miss Loading block from memory is optional
a) Write allocate
Load block from memory into cache, then overwrite
b) Write non-allocate
Overwrite memory directly
Types of misses
Cold cache
Cache hasn’t been in use and is therefore empty.
- Cold miss every (read) memory access that is a cache-miss
Warm cache
Cache has been in use.
- Capacity miss entire cache full - some lines must be evicted
- Conflict miss specific line is full (not necessarily the whole cache) - must be evicted
Hit-rate, miss-rate
Memory references divided by number of instructions that hit or miss the catch.
Eviction (removal) from cache
When there is a capacity or conflict miss, the cache evicts line to make room for new one.
For direct mapping caches we use the mapping.
For associative caches:
LRU least recently used
LFU least frequently used
Random replacement
Cache impact on performance
Cache usually maintained in hardware (”free lunch”).
The cache impacts the sequential and parallel performance.
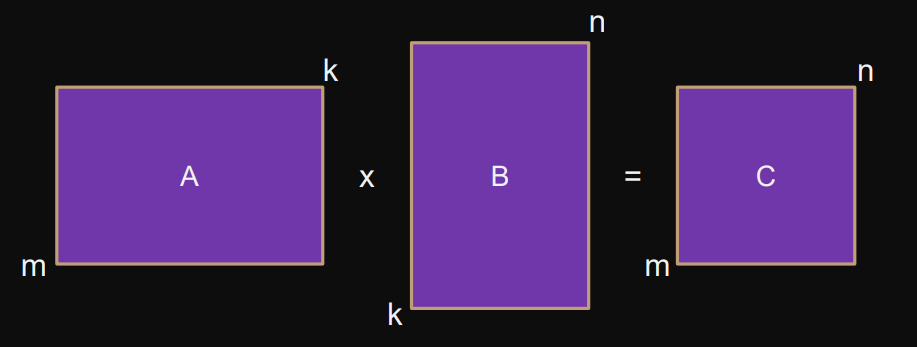
Example: Matrix-Matrix multiplication
Matrix-Matrix multiplication
(associative, distributive but not commutative)
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
C[i][j] = 0;
for (k=0; k<n; k++) {
C[i][j] += A[i][k]*B[k][j];
}
}
}Simple implementation based on mathematical definition (not the best).
Work
Complexity where
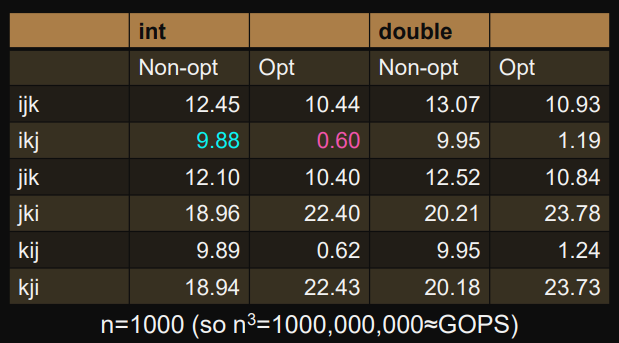
Interchanging loops impacts the performance
The 3 loops can be interchanged: possible variations.
worst performance: as the innermost loop (jki, kji)
for (k=0; k<n; k++) { for (j=0; j<n; j++) { for (i=0; i<n; i++) { C[i][j] += A[i][k]*B[k][j]; } } }B[k][j]is independent ofi.Each iteration is 1 load for
A[i][k]and 1 store forC[i][j]:they both are cache misses (assuming cache can store 2 matrix rows at most).
medium performance: as the innermost loop (ijk, jik)
for (i=0; i<n; i++) { for (j=0; j<n; j++) { C[i][j] = 0; for (k=0; k<n; k++) { C[i][j] += A[i][k]*B[k][j]; } } }C[i][j]is independent ofk(update in register by compiler).Each iteration is 2 loads for
A[i][k],B[k][j]and 1 store forC[i][j]:each load of
B[k][j]is a cache miss because the matrix is accessed in row order.
best performance: as the innermost loop (ikj, kij)
// initialize C[i][j] = 0;for (i=0; i<n; i++) { for (k=0; k<n; k++) { for (j=0; j<n; j++) { C[i][j] += A[i][k]*B[k][j]; } } }A[i][k]is independent ofj(update in register by compiler).Each iteration is 1 load for
B[k][j]and 1 store forC[i][j]:Both are accessed in row order and the miss-rate is given by the cache-line size.
The spatial and temporal locality is exploited well.
This is because how C stores matrices.
Scanning the matrix in row order reduces the number of main-memory-accesses.
We load blocks of 8-16 elements into the cache.
If row > cache, next row forces eviction.

Parallelization
loops fully independent (data parallel).
loop should be in increasing order (unless commutativity of is exploited)
par (0<=i<n, 0<=j<n) {
C[i][j] = 0;
for (k=0; k<n; k++) {
C[i][j] += A[i][k]*B[k][j];
}
}Recursive solution
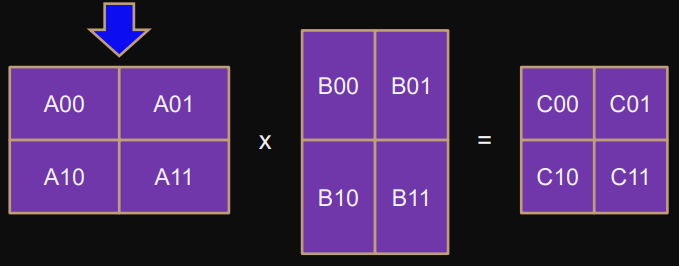
Alternative solution: recursive
Recursively splitting matrices in half in both dimensions.
Each recursion level has 8 submatrix multiplications, 4 submatrix additions:
C00 = A00 * B00 + A01 * B10
C01 = A00 * B01 + A01 * B11
C10 = A10 * B00 + A11 * B10
C11 = A10 * B01 + A11 * B11Calculated using the master theorem
Work
number of nodes in an matrix-multiplication DAG
Time
length of the longest path
Cache behavior
Good - can be made cache oblivious (Good cache behavior is independent of actual cache size).
Can be made cache-aware : multiplying smaller matrices of size so that they fit in cache (based on cache hierarchy).
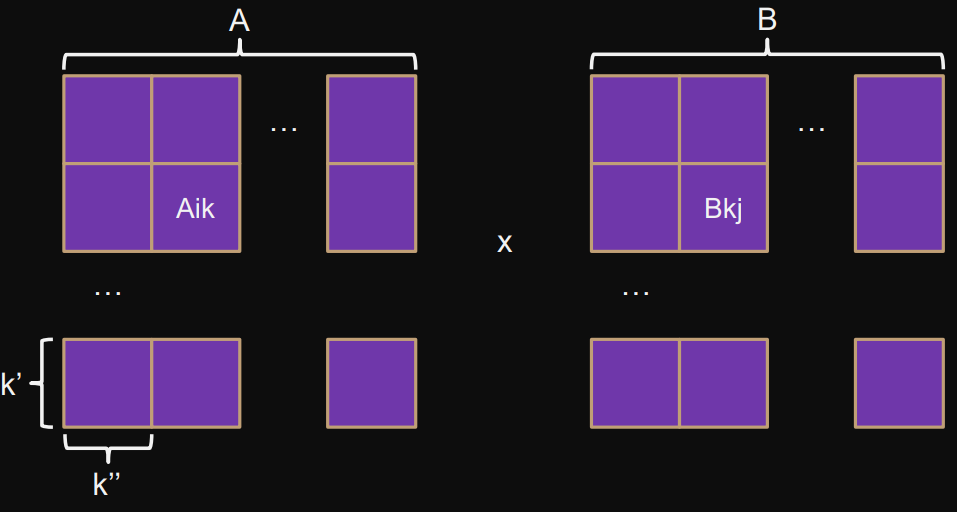
Implementation in C
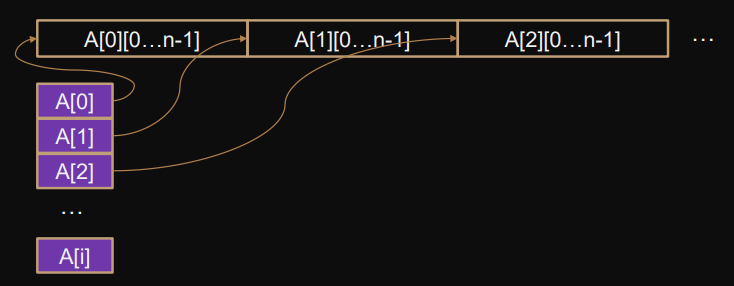
Two dimensional arrays are pointers:
ie:
A[0][0 ... n-1]is between the pointersA[0]andA[1].We therefore represent each submatrix as
A[m0 ... m1][k0 ... k1].Result matrices ie.
c0have size(m1-m0)x(n1-n0).For the recursive calls submatrices are computed using offsets
mo,no.The recursion is stopped when the smallest matrix has size
m1-m0 < CUTOFF(determined experimentally).void MM( double A[][], double B[][], int m0, int m1, int k0, int k1, int n0, int n1, double C[][], int mo, int no // offset in c0, c1 ) { if (/*n0,n1,k0,k1,m0,m1 too small: CUTOFF*/) { BaseMM(A,B,m0,m1,k0,k1,n0,n1,C,mo,no); // call other function with all args} else { double c0[m1-m0][n1-n0]; // output of top half of B double c1[m1-m0][n1-n0]; // output of bottom half of B// A (left-top quad) vs. B (top half) --> C0 (top half) MM(A, B, m0, (m0+m1)/2, k0, (k0+k1)/2, n0, (n0+n1)/2, c0, 0, 0); MM(A, B, m0, (m0+m1)/2, k0, (k0+k1)/2, (n0+n1)/2, n1, c0, 0, (n1-n0)/2);// A (right-top quad) vs. B (bottom half) --> C1 (top half) MM(A, B, m0, (m0+m1)/2, (k0+k1)/2, k1, n0, (n0+n1)/2, c1, 0, 0); MM(A, B, m0, (m0+m1)/2, (k0+k1)/2, k1, (n0+n1)/2, n1, c1, 0, (n1-n0)/2); // A (left-bottom quad) vs. B (top half) --> C0 (bottom half) MM(A, B, (m0+m1)/2, m1, k0, (k0+k1)/2, n0, (n0+n1)/2, c0, m1-m0, 0); MM(A, B, (m0+m1)/2, m1, k0, (k0+k1)/2, (n0+n1)/2, n1, c0, m1-m0, (n1-n0)/2);// A (right-bottom quad) vs. B (bottom half) --> C1 (bottom half) MM(A, B, (m0+m1)/2, m1, (k0+k1)/2, k1, n0, (n0+n1)/2, c1, m1-m0, 0); MM(A, B, (m0+m1)/2, m1, (k0+k1)/2, k1, (n0+n1)/2, n1, c1, m1-m0, (n1-n0)/2);// C = c0 + c1 (using offset) for (i=m0; i<m1; i++) { for (j=n0; j<n1; j++) { C[mo+i][no+j] = c0[i-m0][j-n0] + c1[i-m0][j-n0]; } }... free memory of c0 and c1 } }Call with
MM(A,B,0,m,0,k,0,n,C,0,0);All MM calls are independent.
Cache coherence
Example: caches that are not coherent
Core 0, 1 have private caches and both loaded address .
- Core 0 writes to
- Core 1 wants to read but has a different value
Definition: cache coherence
Let order of memory accesses to specific address be given by program order.
- If processor writes to and no other writes occur (by any processor) before its next read of - then it must read the value it first wrote to .
- If writes to and no other writes occur (by any processor) afterwards until reads - then must read the value first wrote to .
- If and write to at the same time, then only one write is stored at .
More formal definition
- If processor writes to at time and reads at , and there are no other writes (by or other) to between and , then reads the value written at .
-
If
writes to
at
and another
reads a at
and no other
writes to
between
and
, then
reads the value written by
at
.
But there must be sufficient space between and until the updates become visible (there is no absolute time and nothing is immediate).
-
If
and
write to
at the same time, then either the value of
or the value of
is stored at
.
Same time means “sufficiently close” in time - the writes must be “serialized”.
ccNUMA-Systems
(most multi-core and symmetric multiprocessing SMP nodes)
Cache coherence at cache-line-level, maintained by hardware-protocols.
This negatively impacts the performance: bus/network traffic, protocol overhead, transistors and power.
Note: Not all systems are cache coherent (ie. NEC Vector computers)
False sharing
Sharing / false sharing
Cache coherence is maintained at cache-line-level.
Two different addresses are written to cache - but the entire cache-line must be updated.
Avoiding false sharing
Simple, shared variables updated by different threads should be in different cache-lines.
Solutions:
- Simple local variables → compiler might put them in different cache lines
- Pad data-structures (ie. padded array) → wastes a lot of memory

Example 1) unnecessary update
are both in the same cache-line.
core0 updates in a loop, core1 updates in a loop.
Although are in different memory locations, each update will cause a cache coherency activity (although unnecessary).
Variables are called “falsely shared”.
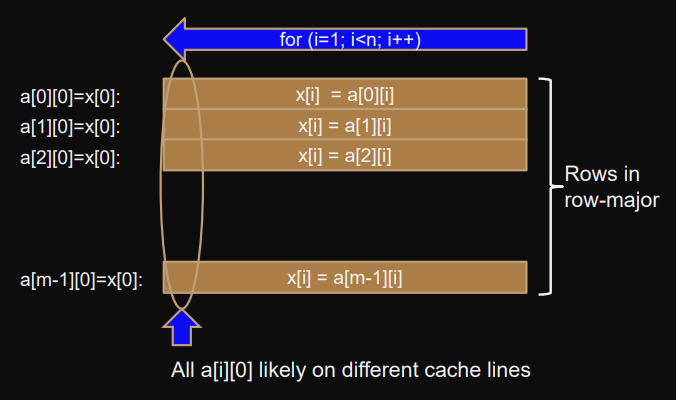
Example 2) storing sum of rows: row-major
Storing row sums at index in matrix:
Matrix is stored row-major in C.
Therefore all are most likely in different cache lines.
The rows and are not spatially close and wont be updated based on eachother.
// a[m][n] two dimensional matrix
int *a = (int*)malloc(m*n*sizeof(int));// row order access
#pragma omp parallel for
for (j=0; j<m; j++) {
int *x = a+j*n; // get address of row
int i;
for (i=1; i<n; i++) { // sum all elements of row and store in [0]
x[0] += x[i];
}
}
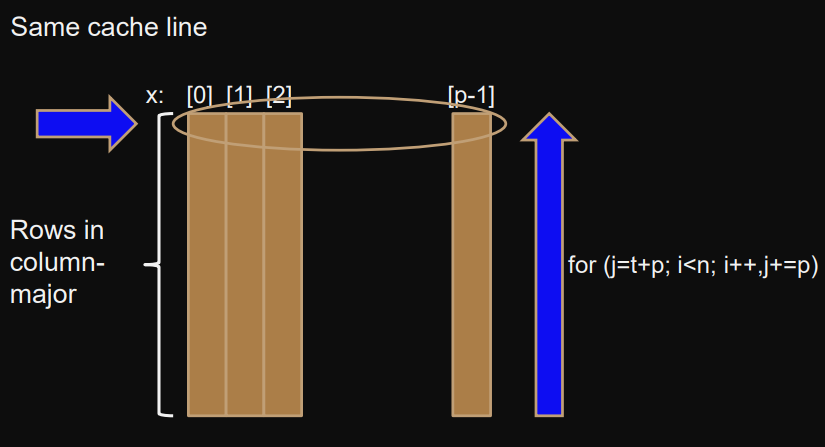
Example 3) storing sum of rows: col-major
same problem as above
Matrix is stored col-major in FORTRAN.
Therefore all are most likely in the same cache line and are updated times.
// x[m][n] two dimensional matrix
int *a = (int*)malloc(n*m*sizeof(int));// row order access
#pragma omp parallel { // assuming p = m
int t = omp_get_thread_num(); // thread id
int i, j;
int *x = a;
for (j=t+p, i=1; i<n; i++,j+=p) {
x[t] += x[j];
}
}implementation with variable
should have no false sharing (as the original FORTRAN implementation).
But compiler might put the variable in a different cache-line.
// x[m][n] two dimensional matrix int *a = (int*)malloc(n*m*sizeof(int));// row order access #pragma omp parallel { int t = omp_get_thread_num(); // thread id int i, j; int *x = a; register int sum = 0; for (j=t+p, i=1; i<n; i++,j+=p) { sum += x[j]; } x[t] = sum; }
NUMA memory performance
Memory (”von Neumann”) bottleneck in NUMA
The memory access times are non-uniform:
Memory closer to a core is faster than memory on another CPU
other problems
- Connection to memory via memory controllers (prefered by memory in bank)
- Less memory controllers than cores and they all share the same memory bandwidth

First touch
Applications try to allocate memory from closer to cores.
“First-touch” OS support:
“The first core (thread) to touch a virtual memory page will cause the virtual page to be allocated in memory close to that core”
This also means that threads that allocate later, are forced to use memory farthest away (remote instead of local).
Latency hiding techniques
These techniques hide latency, but bandwidth must still be suitable for memory requests.
Prefetching
Start loading operands well before use.
Multi-threading (via hardware or software)
switching between virtual processors when a thread requests data and coming back when data arrived.
(requires explicit parallel instruction computing EPIC)
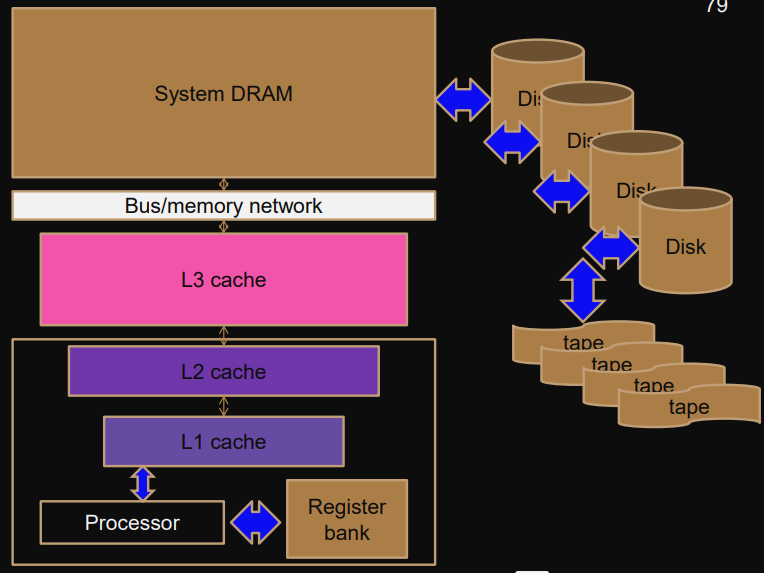
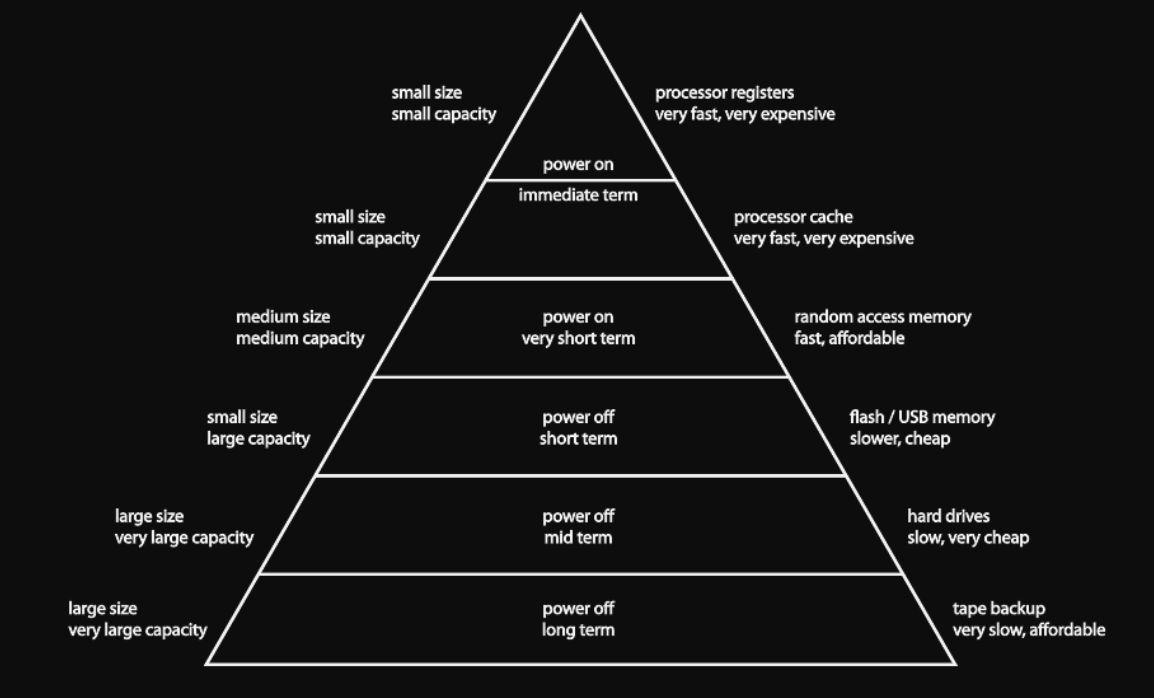
Memory hierarchy and latency
Registers 0 cycles
L1 cache 1 cycle
L2 cache 10 cycles
L3 cache 30 cycles
Main memory 100 cycles
Disk 100.000 cycles
Tape 10.000.000 cycles
Super-linear speedup
Super-linear speedup is impossible — Previous proof: simulation argument
Simulation argument: linear/perfect speedup is the best possible.
Simulation argument assumes that parallel and sequential processors behave similarly = same memory behavior.
This is not true for real systems with a deep memory hierarchy.
Definition
single processor input size , has access to deep memory hierarchy
multiple processors input size , each have full access to main memory and cache
number of memory references
avg time per reference for a single processor (deep hierarchy)
avg time per reference for a single processor in parallel system (flat hierarchy)
If performance is defined by cost of memory references:
Example
(independent of )
This would give us super a super-linear speedup
(wrong term, since its linear but greater than ).
Application performance and memory system
Bounds for applications (”roofline performance / estimate model”)
Memory bound time operating on data < time reading/writing data
Compute bound time operating on data > time reading/writing data
formal definition
Given Implementation on multi-core system:
performance = ie. in operations/s or other measure
operational intensity = average num of operations per byte read/written
memory bandwidth
is memory bound, if
is compute bound, if
example
memory bound algorithms
Merge, prefix-sums → few operations per byte
less memory bound algorithms
Matrix-matrix multiplication → operations on data
Example: Assuming prefix sums performs
= 1/16 FLOP per Byte
1 FLOP per 8 Byte word read and written (16 Bytes)
= 2 GFLOPs
Then it is memory bound is bandwidth is < 32GByte/s.
If memory bound , speedup is limited by memory bandwidth (= How much faster can cores read/write than only one core?)
Program order and memory consistency
Execution-order is not always program-order.
Sequential program order
Sequential consistency
Parallel program order
processors execute some interleaving of parallel program (SPMD or MIMD).
Possible: sequential consistency, relaxed consistency
example
a = 1; a = 2; // last assignment to a b = 3; // last assignment to bb = 7; // last assignment to b a = 1; a = 2; // last assignment to aPossible outcomes:
a = 2,b = 3
a = 2,b = 7
Impossible outcomes:
a = 1,b = 3
Consistency models
Memory consistency (Problem)
What view do threads have of the memory?
In what order do writes to different locations in memory become visible to other cores?
example
x = 0; // … some code x = 1; if (y==0) { // body }y = 0; // … some code y = 1; if (x==0) { // body }Question: can core0 and core1 both execute the body of the if-statement?
Answer:
No, because they each flip the other variable from 0 to 1 before being able to enter the body.
If both variables are flipped to 1 then no body is executed → therefore this is not a good lock-algorithm.
Assuming that
x,yare not in cache of any core:The answer is only valid under the assumption that the writes to the memory are not delayed - else we won’t get an interleaving of the two programs.
Sequential consistency
Outcome of parallel program = execution of some interleaving of the memory accesses of all processors .
Memory operations of each processor:
- take effect immediately
- performed in program-order
Easy to prove properties of programs or reason about correctness (ie. with invariants).
Is guaranteed by hardware (caches, write buffers, ... are logically transparent) .
Sequential consistency not guaranteed by modern multiprocessors because it reduces performance.
In modern multiprocessors (ie. x86, POWER, SPARC):
- Caches may delay writes
- Write buffers may delay and/or reorder writes
- Memory network may reorder writes
- Compiler may reorder updates
Relaxed consistency
loads = reads, stores = writes
May permit:
- Reordering loads after loads
- Reordering loads after stores
- Reorderung stores after loads
- Reorderung stores after stores
Weaker constraints on hardware.
More difficult to prove properties of programs or reason about correctness.
example
Initial value:
flag = falsewhile (!flag) { } a = otherval;otherval = 42; flag = true;Under sequential consistency:
the outcome is
a == 42Under relaxed consistency:
Writes could be reordered and any old value could be stored in
a.Compiler won’t attempt move assignment to
abefore loop but might remove the loop altogether. (Declare boolean flag asvolatile).This can be solved with a fence: Completes all writes executed before the fence and sets flag
f.while (!flag) { } fence; a = otherval;otherval = 42; fence(&flag);
Programming models for memory
Memory fences and memory barriers enforce pending operations to complete.
Fence = local operation for a core
Barrier = involves all processors
Memory fence
Programming model (memory model)
Synchronization/coordination construct to enforce a specific set of interleavings:
fence;
flushes
all
write buffers.
example
x = 0; fence; // so core1 can enter // … some code x = 1;fence; // so core1 can't enter if (y==0) { // body }y = 0; fence; // … some code y = 1;fence; if (x==0) { // body }