Merging

Definition

Problem

data dependent, adaptive, load balancing - problem

Input:

Array $\small A$ of size $\small n$ , Array $\small B$ of size $\small m$

both are sorted - $\small A[i] \leq A[i+1]$ for all $\small 0\leq i \leq (n-1)$

Output:

Array $\small C$ of size $\small n+m$ containing every single element from $\small A, B$

sorted - $\small C[i] \leq C[i+1]$ for all $\small 0\leq i \leq (n+m-1)$

Theorem

on “shared memory system” we can achieve parallel time:

$\color{pink} \small \text{Tpar}(p, n+m) \in O((n+m)/p+\log n)$

(Convenient to assume “shared-memory programming model” → in “distributed memory programming model” we would need communication and data redistribution)

Distinctness

Sometimes useful to assume that all elements are distinct.

Assumption does not reduce generalizability: We can make elements distrinct through lexicographical ordering of pairs $\small (A[i], i)$ :

If $\small A[i] \leq A[j]$ and $\small i <j$ then: $\small (A[i], i) < (A[j],j)$

This means, when they are equal, the index decides which one is considered larger

Disadvantage: more memory usage

Stable merge

When original index-order of equal input-elements is preserved in output array.

Stability sometimes desirable ie. Radix sort

Strictly sequential solution

this is not the best known solution

$\color{pink} \small \text{Tseq}(n+m) \in O(n+m)$

$\small (n+m)$ read and write operations in total

i = 0; j = 0; k = 0;// pick smaller elem from both arrays
while (i<n && j<m) {
C[k++] = (A[i]<=B[j]) ? A[i++] : B[j++];
}// fill up the rest, if one array is already eliminated
while (i<n) C[k++] = A[i++];
while (j<m) C[k++] = B[j++];

Merging by Ranking

$\small \tt rank(x,A)$

= number of elements in $\tt A$ that are smaller than $\tt x$

Can be done sequentually in ordered arrays with binary search $\small O(\log n)$

$\small A[i]$ written in $\small C[i+\texttt{rank}(A[i], B)]$

$\small B[j]$ written in $\small C[j+\texttt{rank}(B[j], A)]$

👉

rank(A[pos], B) can be understood as the index of the first element in B that is bigger than A[pos]

Barrier pattern

Synchronization pattern

Explicit synchronization through barrier

At barrier the processor can’t continue until others have also reached that point.

Solution 1)

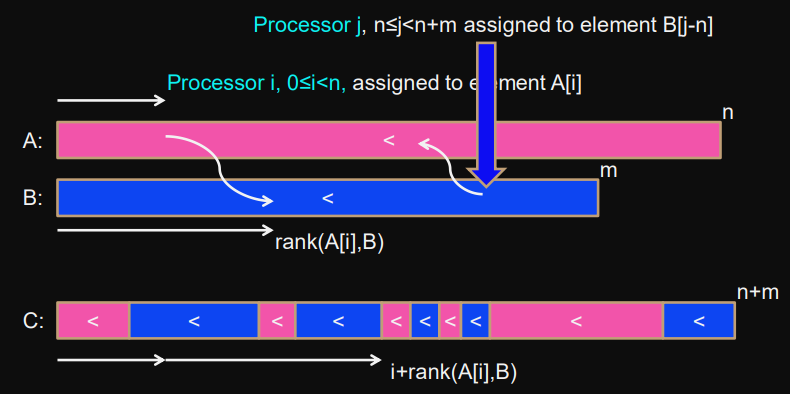
Explicit paralelization: We tell each processor what to do

One processor per element: $\small p = n+m$

Processor $\small i, \quad 0\leq i < n$ assigned to $\small A[i]$

Processor $\small j, \quad n\leq j< n+m$ assigned to $\small B[j-n]$

par (0 <= i < n+m) {
if (i < n) {
// Array A
C[i+rank(A[i],B)] = A[i];} else if (i < n+m) {
// Array B
j = i-n;
C[j+rank(B[j],A)] = B[j];
}barrier; // synchronization construct so that any C[k] can be accessed
}

The algorithm is not efficient:

$\color{pink} \small \text{Tpar}(n+m, n+m) \in O(\log(\max(n,m)))$

Exponential improvement in time with linear number of processors

$\small \textcolor{pink} {\text{Wpar}(n+m, n+m) \in }O((m+n)\cdot \log(\max(m,n))) \leq O(2n \log n) = \textcolor{pink} {O(n\log n)}$

Not work-optimal

$\small \textcolor{pink} {S_p(n) = }\large \frac{\text{Tseq}(n)}{\text{Tpar}(p,n)} \small = \large \frac{ n+m}{\log(\max(m,n))} \small = \dots = \textcolor{pink} {O(n / (n \log n) / p) = O(p / \log n)}$

Speedup is bad. It decreases with with $\small n$ .

Normally $\small n \gg p$

Solution 2)

👉

Improve performance

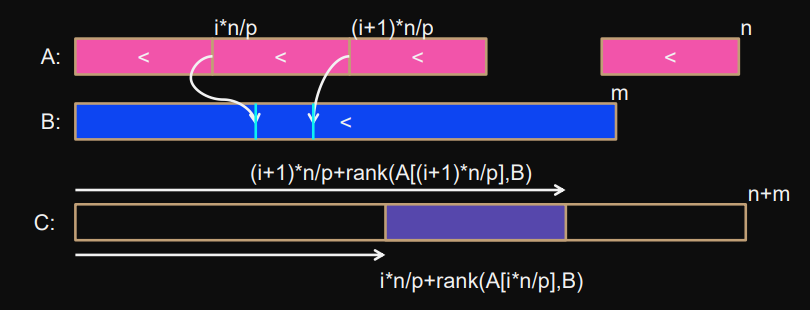
Solution 2)

Divide $\small A$ into blocks of $\small \approx n/p$ , then rank the start and end of each block.

We find the matching block in $\small B$ for each block in $\small A$ .

Number of processors does not depend on Input.

Assumes $\small n$ is divisible by $\small p$ (can be fixed if not the case).

We then merge blocks of $\small A,B$ sequentially.

$\small \tt merge$ and $\small \tt rank$ are sequential algorithms.

par (0 <= i < p) {
pos = i*(n/p);
nextPos = (i+1)*n/p;// sequential merge
merge (
// & → Address of ...
&A[pos],                               // interval start in A
n/p,                                   // n (interval size in A)
&B[rank(A[pos],B)],                    // interval start in B
rank(A[nextPos],B) - rank(A[pos],B),   // m (interval size in B)
&C[pos + rank(A[pos],B)]               // interval start in C
);
barrier;
}

$\color{pink} \small \text{Tpar}(p,n+m) = O(n/p+m+\log n)$

There can be severe load imbalance where one processor does all the work, because the intervall in $\small A$ gets mapped to a huge chunk in $\small B$ .

$\small \textcolor{pink} {\text{Wpar}(p,n+m) =} O(p \log m + p \cdot (n/p)+m) = O(p \log m + (n+m)) = \textcolor{pink} {O(n+m)}$

Work-optimal for $\small p \leq \large \frac{m+n}{\log m}$

Solution 3a)

👉

Fix load imbalance

Solution 3a)

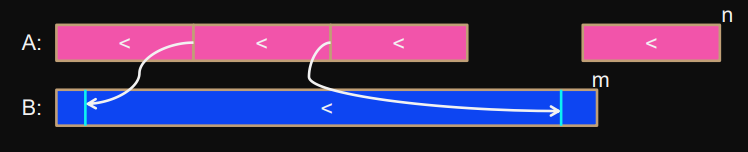
Divide $\small A$ into blocks of $\small \approx n/p$ , then rank the start and end of each block.

Differentiate between good and bad segments in $\small B$ :

good segments :rank(A[nextPos],B)-rank(A[pos],B)≤ m/p

balanced pairs

Do sequential merge

bad segments :rank(A[nextPos],B)-rank(A[pos],B)> m/p

unbalanced pairs → divide intervall in $\small B$ into smaller blocks and find their partner-block in $\small A$ (means also splitting $\small A$ up) .

This way wereassignprocessors to the start-indices of the blocks which is problematic.

In case there is more than one bad segment we use prefix-sums (see below).

This way there are at most $\small p$ smaller merge-pairs all of size $\small O(n/p+m/p)$

One old block in $\small A$ now can get multiple partner blocks in $\small B$ in case the block in $\small B$ has a size $\small > m/p$ .

Solution 3b)

👉

Avoid load imbalance

Solution 3b)

Divide $\small A$ into blocks of $\small \approx n/p$

Divide $\small B$ into blocks of $\small \approx m/p$

This gives $\small p$ independent merge-pairs all of size $\small O(n/p+m/p)$

Experience shows that the pairs are usually independent from eachother (but we could potentially do twice the work).

One block can get mapped to an intervall outside of its partner-block

Merging by Co-ranking

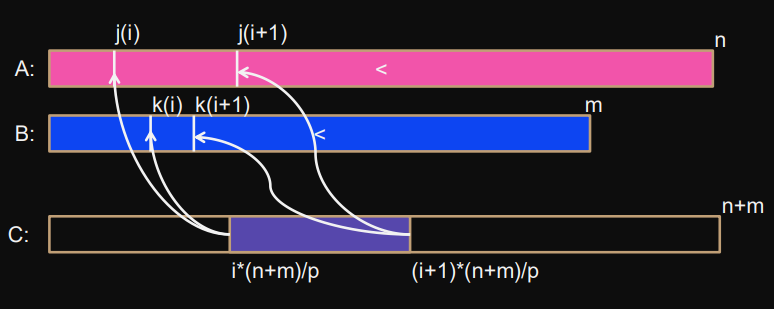
Co-Ranks

j(i), k(i) are the co-ranks of segment i

A[j(i), j(i+1)-1] and B[k(i),k(i+1)-1]— merged —→C[i*(n+m)/p, (i+1)*(n+m)/p-1]

They satisfy: j(i) + k(i) = i*(n+m)/p

💡

Co-Ranks can be understood as the indices in A , B from which the merging of segment i(with indexi*(n+m)/p) starts.

Example
A[j(i), j(i+1)-1]andB[k(i),k(i+1)-1]— merged —→C[i*(n+m)/p, (i+1)*(n+m)/p-1]
```
A [0, 2, 4, 6]
B [1, 3, 5, 7]
\___/  \___/
0      1     <- segments (for each processor)C [0, 1, 2, 3, 4, 5, 6, 7]
\_________/  \_________/
0            1       <- segments (for each processor)
```
Lets say we have 2 processors p = 2 and each of them gets a segment of C :
n = 4 , m = 4→ Length of each segment: (n+m)/p = 4
We calculate the beginning and end of the segment dedicated to each processor:
p_0 dedicated to segment i=0 : C[0*(n+m)/p; 1*(n+m)/p-1] =C[0;3]
p_1 dedicated to segment i=1 : C[1*(n+m)/p; 2*(n+m)/p-1] =C[4;7]
We want to find the pair-segments from A, B that will be merged into our segment in C :
🪄 magic calculation
For i = 0
j(0) = 0
k(0) = 0
Check of invariant: j(0) + k(0) = 0*(n+m)/p = 0
For i = 1
j(1) = 2
k(1) = 2
Check of invariant: j(1) + k(1) = 1*(n+m)/p = 4
For i = 2
j(2) = 4
k(2) = 4
Check of invariant: j(2) + k(2) = 2*(n+m)/p = 8
Now we know:
i = 0 → C[0;3] is merged from
A[j(0); j(0+1)-1] and B[k(0); k(0+1)-1]
A[0; 1] and B[0; 1]
i = 1 → C[4;7] is merged from
A[j(1); j(1+1)-1] and B[k(1); k(1+1)-1]
A[2; 3] and B[2; 3]

Co-Rank Lemma

Let i be a shorthand for: (i)*(n+m)/p(same applies for co-ranksj,k)

Let (i)-1 be a shorthand for: (i)*(n+m)/p-1

Let i-1 be a shorthand for: (i-1)*(n+m)/p(same applies for co-ranksj-1,k-1)

For any i in 0 ≤ i < n+m there are unique j , k such that:

j + k = i

Either k = 0 or A[(j)-1] ≤ B[k]

Either j = 0 or B[(k)-1] < A[j]

merge(A[0,…,(j)-1], B[0,…,(k)-1]) = C[0,…,i-1]

Proof of lemma
1. Invariant
  j + k = i
1. Transivity
  C[(i')-1] ≤ C[(i)-1] ≤ C[(i'')-1] for any i' , i'' with i' < i < i''
  Because of
  1. A[j-1; (j)-1] ∈ C[0; (i)-1]
    B[k-1; (k)-1] ∈ C[0; (i)-1]
    more precisely:∈ C[i-1; (i)-1]
  1. A[j], B[k] ∉ C[0; (i)-1]
  The last element C[(i)-1] must either be from A or B :
  1. If A gets chosen:
    C[(i)-1] = A[(j)-1] $\small \implies$ A[(j)-1] ≤ B[k] or else an element from B would have been chosen.
    B[(k)-1] < A[(j)-1] ≤ A[j] $\small \implies$ B[(k)-1] < A[j]
  1. If B gets chosen:
    C[(i)-1] = B[(k)-1] $\small \implies$ B[(k)-1] < A[j] or else an element from A would have been chosen.
    Same as above: A[(j)-1] ≤ B[k]

Co-Rank Algorithm

Very similar to binary search.

j = min(i,n);
k = i-j;
jlow = max(0,i-m);done = 0;
do {
// case 1: j is too large
if (j>0 && k<m && A[j-1]>B[k]) {
d = (1+j-jlow)/2;
klow = k;
j -= d;
k += d;
// case 2: k is too large
} else if (k>0 && j<n && B[k-1]>=A[j]) {
d = (1+k-klow)/2;
jlow = j;
k -= d;
j += d;
} else {
done = 1;
}
} while (!done)

First assume C is made out of only elements from A first:
j = min(i, n)
k = i-j

If A[(j)-1] > B[k]
then j was too large → we should have chosen element fromB
now halve j and increase k → we needjlowfor this
j=(j-jlow)/2
klow = old value of k

If B[(k)-1] ≥ A[j]
then k was too large → we should have chosen element fromA
now halve k and increase j → we needklowfor this
k = (k-klow)/2
jlow = old value of j

Iterate $\small O(\log(n+m))$ times until lemma is satisfied

Solution 4)

👉

Perfectly load balanced: Turning upside-down and merging by co-ranking

Solution 4)

Each processor handles a segment of $\small C$ of the same size.

Perfectly load-balanced, stable.

Divide $\small C$ of size $\small (n+m)$ into $\small p$ blocks of size $\small (n+m)/p$ .

This means i ∈ [0; p-1]

The start index of block is i*(n+m)/p

For each block $\small i$ :

Determine its co-ranks j(i), k(i) and store into coj[i], cok[i] .

Merge the blocks A[j(i); j(i+1)-1] and B[k(i); k(i+1)-1] into
C[i*(n+m)/p; (i+1)*(n+m)/p-1]

par (0 <= i < p) {
// 1) get coranks
// coj[]: array of j-coranks
// cok[]: array of k-coranks
corank(i*(n+m)/p, A, n, &coj[i], B, m, &cok[i]);
barrier; // processor i will need coranks of i+1
// 2) merge (sequentially)
merge(
&A[coj[i]],           // interval start in A
coj[i+1] - coj[i],    // n (interval size in A)
&B[cok[i]],           // interval start in B
cok[i+1] - cok[i],    // m (interval size in B)
&C[i*(n+m)/p]         // interval start in C
);barrier;
}

$\small \textcolor{pink}{\text{Wpar}(p,n+m) \approx }p \cdot O(\frac{n+m}{p} + \log (n+m)) = \textcolor{pink}{O(n+m+p \cdot \log(n+m) )}$

which is $\small O(n+m)$ when $\small (p \cdot \log (n+m)) \in O(n+m)$ .

Work optimal

We can also get rid of the first synchronization barrier

It is necessary because process $\small i$ requires co-ranks of process $\small i+1$ .

implementation

Cost: Redundant computation of coranks, more memory

par (0 <= i < p) {
// 1) get coranks -> not arrays but variables j1, j2, k1, k2
corank(i*(n+m)/p, A, n, &j1, B, m, &k1);
corank((i+1)*(n+m)/p, A, n, &j2, B, m, &k2); // compute again
// 2) merge (sequentially)
merge(
&A[j1],          // interval start in A
j2 - j1,         // n (interval size in A)
&B[k1],          // interval start in B
k2 - k1,         // m (interval size in B)
&C[i*(n+m)/p]    // interval start in C
);barrier; // not needed anymore
}