OpenMP
Perfect tutorial: https://www.openmp.org/wp-content/uploads/OpenMP-4.0-C.pdf
OpenMP
= Standard for data parallel, shared memory programming (parallel thread programming).
Uses pragma constructs.
Pragma constructs
#pragma omp <directive> [clauses]Each directive / construct has clauses.
Clauses can modify, restrict, extend a construct.
Models
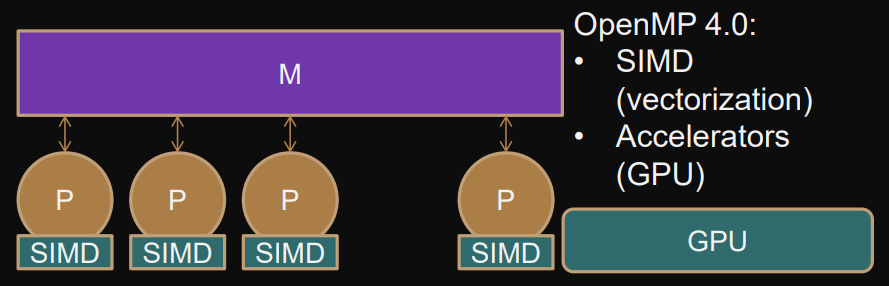
OpenMP architecture model
Multi-core, fixed number of cores, multilevel cc-NUMA
Naive, flat, shared memory model without cost model
OpenMP programming model
-
Parallelism through work-sharing (mostly implicit)
All threads execute same program (SPMD)
-
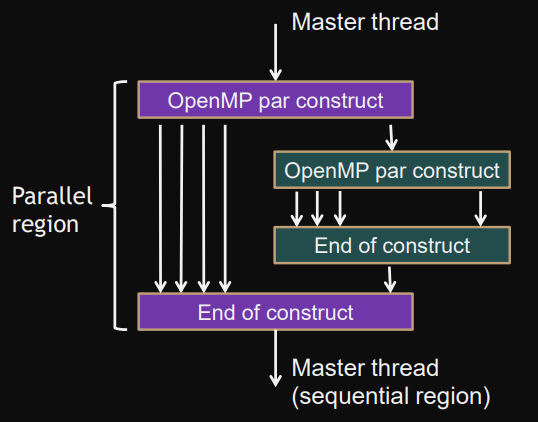
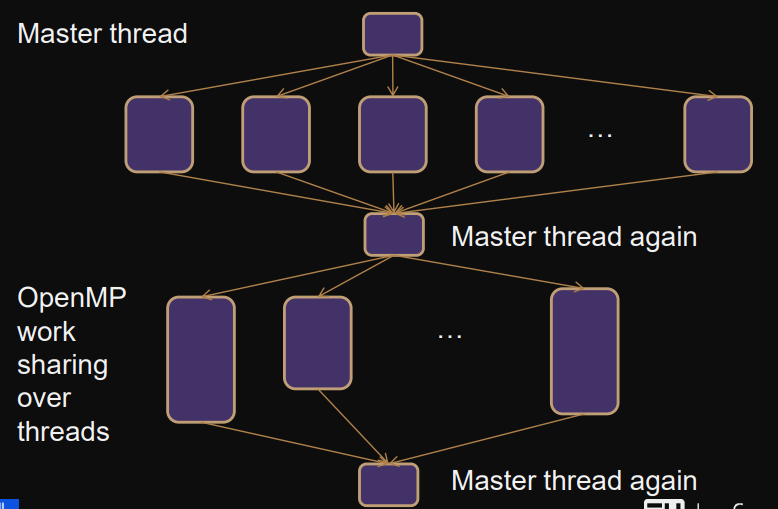
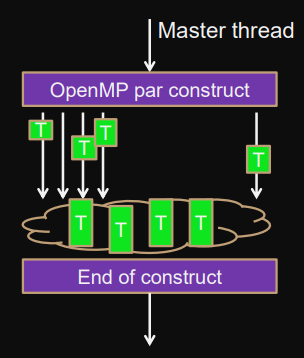
Fork-join parallelism
Master thread implicitly spawns threads through pragma-constructs - threads join at end of construct.
- Threads have unique id in construct
- Number of threads can be > number of processors/cores
- Threads intended to be executed in parallel
- Constructs for sharing work across threads
- Work expressed as loops and task graphs
- Threads use shared variables (shared among all threads)
- Threads use private variables
- Unprotected, parallel updates of shared variables lead to race conditions (bad practice)
- Synchronization constructs for preventing race conditions
Concepts
Work
- Loops of independent iterations
- Task graphs
- Finite sections of graph
Master thread (sequential region)
contains shared variables.
Before entering the master thread again (at the end of construct) there is an implicit barrier.
Parallel region (parallel region)
are where work is shared among threads
contain private variables
can be nested.
Best practice: small number of successive parallel regions.
longest path length
Load balance in regions
Parallel region construct
Parallel region
- controls variable sharing, work sharing among activated threads
-
Lets thread execute asynchronously, with own id
The structured block in construct executed by all threads.
Master thread:
thread_num=0It’s forbidden for a thread to jump into and out of parallel region.
-
Ends with implicit barrier synchronization
then only the master thread is active and memory is in consistent state (All updates to shared variables completed and visible).
#pragma omp parallel [clause ...]
<structured block>
// implicit barrierExample
Iterations of loop must be independent (ie. matrix-vector multiplication)
for (i=0; i<n; i++) { a[i] = f(i); }#pragma omp parallel { int i; int block = n/omp_get_num_threads(); int start = omp_get_thread_num()*block; int end = start+block;for (i=start; i<end; i++) { a[i] = f(i); } }
Clauses
// conditional clause if (scalar_expression)// controlling shared variables private (list) shared (list) default (shared | none) firstprivate (list)reduction(operator: list) // reduction clause copyin(list) num_threads(integer-expression) proc_bind(master | close | spread) // pinning
conditional clause
Evaluated at run-time, limits number of threads.
#pragma omp parallel if (n<=1000) num_threads(2) { ... }
Here: If
(n<=1000)
then fixed number of threads for this region must be
num_threads(2)
else the number of threads in parallel region will be 1.
Example
#pragma omp parallel if (n<=1000) num_threads(2) { int i; int block = n/omp_get_num_threads(); int start = omp_get_thread_num()*block; int end = start+block; for (i=start; i<end; i++) { a[i] = f(i); } }
Work sharing constructs (used inside parallel region)
Work sharing: implicit assignment of pieces of work to threads (scheduling)
sections
Finite number of different tasks can be executed in parallel
single
/
master
Some task should be executed only once
for
Iteration space of loop of independent iterations divided across threads
task
Task graphs
Synchronization
barrier
thread cannot proceed before all other threads have reached the barrier
Shared variables
Controlling shared variables
Shared variables = variables used from master thread, can cause race conditions.
Can be controlled at entry to parallel region:
If pointer declared
private
a local copy of the pointer is created per thread before entering parallel section.
It’s best practice to set
default(none)
shared(<list of vars>)
private(<list of vars>) // private but not initialized
firstprivate(<list of vars>) // private and initialized in masterdefault(shared) // (default mode)
default(none) // sharing mode must be explicit for all shared variablesExample
Not controlled
int *a; a = (int*)malloc(n*sizeof(a*)); // will be shared#pragma omp parallel { int i; int block = n/omp_get_num_threads(); int start = omp_get_thread_num()*block; int end = start+block; for (i=start; i<end; i++) { a[i] = f(i); } }Controlled
int a[200];#pragma omp parallel default(none) private(a) { int i; int block = n/omp_get_num_threads(); int start = omp_get_thread_num()*block; int end = start+block; for (i=start; i<end; i++) { a[i] = f(i); } }
Work sharing constructs
For-construct
for
Data parallel loop scheduled (iteration space set) over available threads.
Implicit barrier at end of block.
#pragma omp parallel {
#pragma omp for
for (i=0; i<n; i++) {
// iterations split
} // implicit barrier
}Syntactic sugar:
#pragma omp parallel forOne can’t remove the second implicit barrier (see example below) because there is no
nowaitclause forparallel.#pragma omp parallel for { for (i=0; i<n; i++) { // iterations split } }
Loop must be in the standardized (canonical) form
Illegal loops:
#pragma omp parallel for for (;;) { // C open loop }#pragma omp parallel for for (i=0; i<n; i++) { if (exceptional(i)) break; // illegal if (i%2==0) continue; // legal }#pragma omp parallel for for (i=0; i<n; i*=2) { a[i] = …; }
Example: remove redundant implicit barrier
#pragma omp parallel { int i; #pragma omp for for (i=0; i<n; i++) { a[i] = f(i); } // implicit barrier} // implicit barrier (again)#pragma omp parallel { int i; #pragma omp for nowait // remove redundant second barrier for (i=0; i<n; i++) { a[i] = f(i); } }
Example: combined with single
#pragma omp parallel { int i; #pragma omp single readarray(b,n); // (executed once - then all threads have same view of b) // implicit barrier here#pragma omp for for (i=0; i<n; i++) { a[i] = b[i]; } // implicit barrier here #pragma omp single nowait writearray(a,n);} // implicit barrier here
Clauses
schedule (type [,chunk]) ordered // don't use private (list) firstprivate (list) lastprivate (list) // copies list back to global from last iteration shared (list) reduction (operator: list) collapse (n) // nested loops nowait // remove implicit barrier at end of construct

SIMD-construct
simd
Single instruction multiple data SIMD / vector parallelism:
Can be mapped to vector operations of hardware
#pragma omp [for] simd {
for (i=0; i<n; i++) {
// iterations split and vector operation
}
}Example: Looping on vectors (arrays)
double a[n], b[n], c[n];#pragma omp simd for (i=0; i<n; i++) { c[i] = a[i]+b[i]; }double a[n], b[n], c[n];#pragma omp parallel for simd // for (i=0; i<n; i++) { c[i] = a[i]+b[i]; }
Clauses
safelen(length) // how much apart concurrent iterations are allowed to be simdlen(length) linear(list[ : linear-step]) aligned(list[ : alignment]) private(list) lastprivate(list) reduction(reduction-identifier : list) collapse(n)
Taskloop-construct
taskloop
Turns chunks of iterations into tasks - runtime decides schedule (can potentially improve).
Can’t use schedule clauses.
#pragma omp taskloopExample
#pragma omp parallel #pragma omp single nowait #pragma omp taskloop collapse(2) for (i=0; i<m; i++) { for (j=0; j<n; j++) { a[i][j] = i+j; } }
Clauses
if([ taskloop :] scalar-expr) shared(list) private(list) firstprivate(list) lastprivate(list) default(shared | none) grainsize(grain-size) // controls size and number of tasks num_tasks(num-tasks) collapse(n) final(scalar-expr) priority(priority-value) untied mergeable nogroup
Task-construct
task
Generates a DAG.
Code sections marked as
tasks
can be suspended (deferred) and later be executed by any thread in the region (by any thread).
All tasks must be completed by end of parallel region.
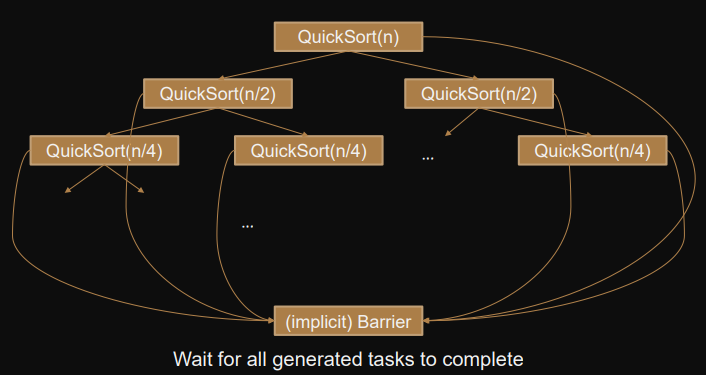
Example: Quicksort
Quicksort calls are independent.
We mark each call as a task and the runtime will spawn them dynamically.
void QuickSort(int x[],int n) { if (n<=1) return;pivot = choosepivot(x,n); ix = partition(x,n,pivot); QuickSort(x,ix); QuickSort(x+ix+1,n-1-ix); }int main(int argc, char *argv[]){ ... #pragma omp parallel { #pragma omp single nowait QuickSort(x,n); // no implicit barrier } // implicit barrier return 0; }void QuickSort(int x[],int n) { if (n<=1) return; pivot = choosepivot(x,n); ix = partition(x,n,pivot); // partition O(n) #pragma omp task shared(x) QuickSort(x,ix); #pragma omp task shared(x) QuickSort(x+ix+1,n-1-ix); //#taskwait <- not needed here, because of implicit barrier (see above) }By using
singleinparallel, we first activate all threads and only use a single one to call the function.We then wait for each task to finish independently based on DAG generated by OpenMP runtime-system.
- Total work over all tasks → Asymptotically same as sequential QuickSort
- Recursion depth with optimal pivot selection:
- Work on critical path:
-
Parallelism:
.
Bottleneck is the partition call.
The QuickSort DAG is “strict” → randomized work-stealing is probably efficient.
Example: Counting occurences in unordered array
int search(int x, int a[], int n) { if (n==1) { return (a[0]==x) ? 1 : 0; } else { int s0, int s1;#pragma omp task shared(s0,a) s0 = search(x, a, n/2); // left half #pragma omp task shared(s1,a) s1 = search(x, a+n/2, n-n/2); // right half #pragma omp taskwait return s0+s1;} }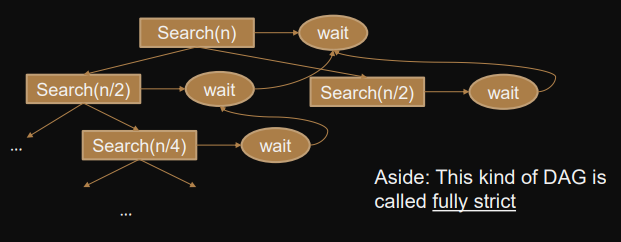
- Total work in DAG
- Recursion depth
- Work on critical path
- Parallelism
Clauses
if(scalar-expression) final(scalar-expression) untied default(shared | none) mergeable // used for small tasks (they might have too much overhead) private(list) firstprivate(list) shared(list) depend(dependence-type : list) priority(priority-value)
Sections-construct
sections
Finite set of sections assigned to threads (scheduled) and executed in parallel.
Scheduling = assigning sections to threads
#pragma omp parallel {
#pragma omp sections
#pragma omp section {
// A
}
#pragma omp section {
// B
}
// …
}Manual solution (inefficient)
We explicitly assign a task to a thread.
#pragma omp parallel if (omp_get_thread_num()==0) { A(…); // do this } else if (omp_get_thread_num()==1) { B(…); // do that } else { … }There can be more sections than threads, then we need scheduling (a thread executes more than one section).
Example: Loop with two independent tasks
int i; float a[N], b[N], c[N], d[N]; for (i=0; i < N; i++) { a[i] = …; b[i] = …; }// assignments to c,d are independent but both depend on a,b for (i=0; i < N; i++) { c[i] = a[i] + b[i]; d[i] = a[i] * b[i]; }int i; float a[N], b[N], c[N], d[N]; for (i=0; i < N; i++) { a[i] = …; b[i] = …; }#pragma omp parallel default(none) shared(a,b,c,d) private(i) { #pragma omp sections nowait { #pragma omp section // Task 1 for (i=0; i < N; i++) c[i] = a[i] + b[i]; #pragma omp section // Task 2 for (i=0; i < N; i++) d[i] = a[i] * b[i]; } }
Clauses
private (list) firstprivate (list) lastprivate (list) reduction (operator: list) nowait // remove implicit barrier at end of construct
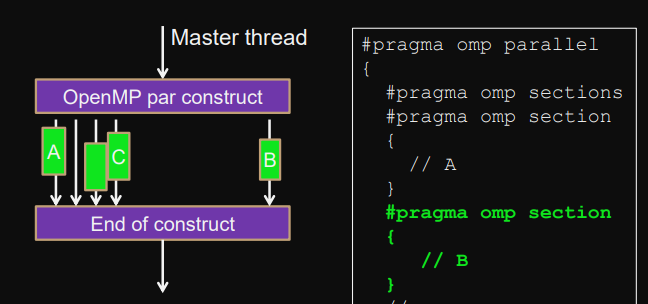
Single-construct
single
Sequential code in parallel construct - only to be executed by a single thread.
No mutual exclusion.
Implicit barrier after block.
#pragma omp parallel {
#pragma omp single {
// some thread
} // implicit barrier
}Example
#pragma omp parallel { int i; int block = n/omp_get_num_threads(); int start = omp_get_thread_num()*block; int end = start+block;#pragma omp single readarray(b, n); // implicit barrier (all threads will have the same view) for (i=start; i<end; i++) { a[i] = b[i]; }#pragma omp barrier#pragma omp single nowait printf("done.");} // implicit barrier
Clauses
private (list) firstprivate (list) nowait // remove implicit barrier at end of construct
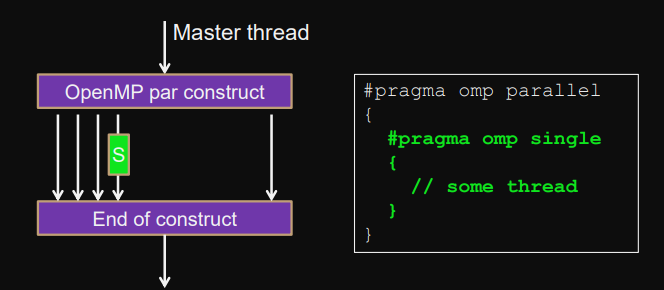
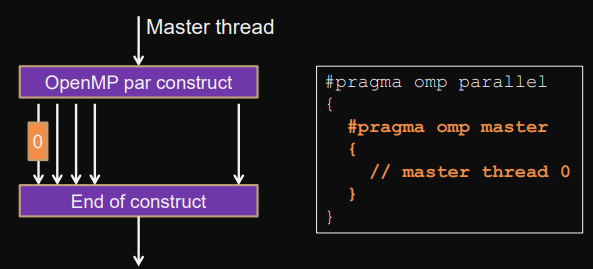
Master-construct
master
Sequential code for master-thread in parallel construct.
No mutual exclusion, no barrier.
#pragma omp parallel {
#pragma omp master {
// master thread 0
}
}Example
#pragma omp parallel { int i; int block = n/omp_get_num_threads(); int start = omp_get_thread_num()*block; int end = start+block;#pragma omp master readarray(b, n); // dangerous! no implicit barrier here // threads won't have the same view -> race condition for (i=start; i<end; i++) { a[i] = b[i]; }#pragma omp barrier#pragma omp single printf("done."); // implicit barrier} // implicit barrier
Clauses
private (list) firstprivate (list) nowait // remove implicit barrier at end of construct
Synchronization constructs
Data-races should be avoided
Parallel threads update an unprotected shared variable so that the outcome of the program dependens on the relative order in which the threads perform their updates.
Compilers can not check whether programs have these race conditions.
barrier
Semantically synchronizes threads.
Can cause deadlock if threads execute part of code that does not contain barrier.
#pragma omp barrierExample: Merging by coranking
// global, read-only values A, B, n, m int j[p+1], k[p+1]; // allocate in advance j[p] = n; k[p] = m;#pragma omp parallel { int i = omp_get_thread_num(); int p = omp_get_num_threads();corank(i*(n+m)/p, A, n, &j[i], B, m, &k[i]); #pragma omp barriermerge( &A[j[i]],j[i+1]-j[i], &B[k[i]],k[i+1]-k[i], &C[i*(n+m)/p] ); }// global, read-only values A, B, n, m #pragma omp parallel { int i = omp_get_thread_num(); int p = omp_get_num_threads(); int j1, k1, j2, k2; corank(i*(n+m)/p , A, n, &j1, B, m, &k1); corank((i+1)*(n+m)/p, A, n, &j2, B, m, &k2); merge( &A[j1], j2-j1, &B[k1], k2-k1, &C[i*(n+m)/p] ); }Trade-off: Explicit barrier saves one corank computation per thread.
It depends on
n,m,pand characteristics of multi-core system which one is cheaper.
taskwait
Used for
task
construct
Waits for completion of generated tasks (children), not transitively for all successor tasks
This optimizes fully strict DAGs
#pragma omp taskwaitcritical
Used to mark a critical section.
Enforces mutual exclusion in code region (always at most 1 thread at a time).
Order with which threads enter critical section is not set.
Updates to shared variables won’t cause a race condition.
#pragma omp critical [(<name>)]Example: Counting accesses
Without mutual exclusion we would get a race condition.
int t = 0;#pragma omp parallel shared(t) #pragma omp critical t++; <-- possible race condition on increment #pragma omp barrier print("Threads so far %d of %d by %d\n", t, omp_get_num_threads(), omp_get_thread_num());
Example: min-max reductions
Sequential algorithm
max = x[0]; min = x[0]; for (i=1; i<n; i++) { if (x[i]<min) min = x[i]; if (x[i]>max) max = x[i]; }Attempt at parallelization
minandmaxare different for each thread → race condition.max = x[0]; min = x[0];#pragma omp parallel for for (i=1; i<n; i++) { if (x[i]<min) min = x[i]; <-- race condition on update of min if (x[i]>max) max = x[i]; <-- race condition on update of max }Solution 1) Reduction
max = x[0]; min = x[0];#pragma omp parallel for reduction (min:min), reduction (max:max) for (i=1; i<n; i++) { if (x[i]<min) min = x[i]; if (x[i]>max) max = x[i]; }Solution 2) Critical section
We check twice (recheck), in case the values change when we enter the if’s-body.
max = x[0]; min = x[0];#pragma omp parallel for for (i=1; i<n; i++) { if (x[i]<min) { #pragma omp critical(MIN) if (x[i]<min) min = x[i]; } if (x[i]>max) { #pragma omp critical(MAX) if (x[i]>max) max = x[i]; } }
opm_set_lock(lock library routines)
Same as pthreds mutex: Dynnamic lock.
Must be allocated/initialized and destroyed again.
No guarantee for fairness.
Library
#include <omp.h> // set void omp_set_lock(omp_lock_t *lock); void omp_set_nest_lock(omp_nest_lock_t *lock);// unset void omp_unset_lock(omp_lock_t *lock); void omp_unset_nest_lock(omp_nest_lock_t *lock);// test int omp_test_lock(omp_lock_t *lock); int omp_test_nest_lock(omp_nest_lock_t *lock);
atomic(atomic operations)
Concurrent and read-modify-write on shared variable in (optimistically).
All updates on shared variable must be atomic.
Atomic = Opeartion can not be interrupted by other threads and completes in finite (bounded) time.
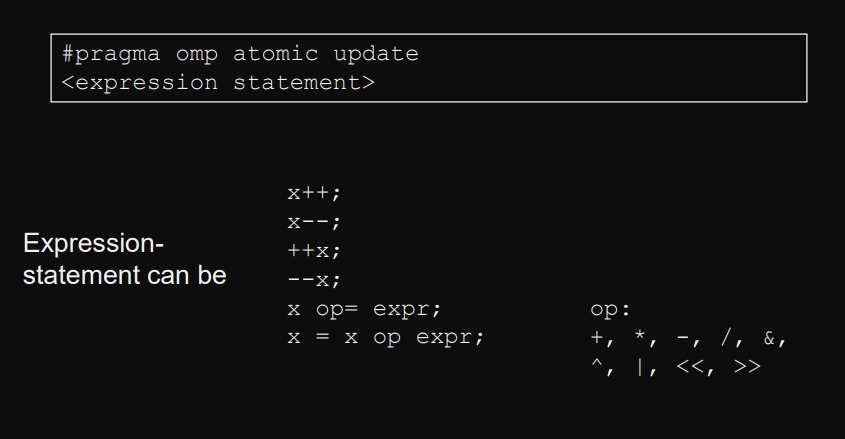
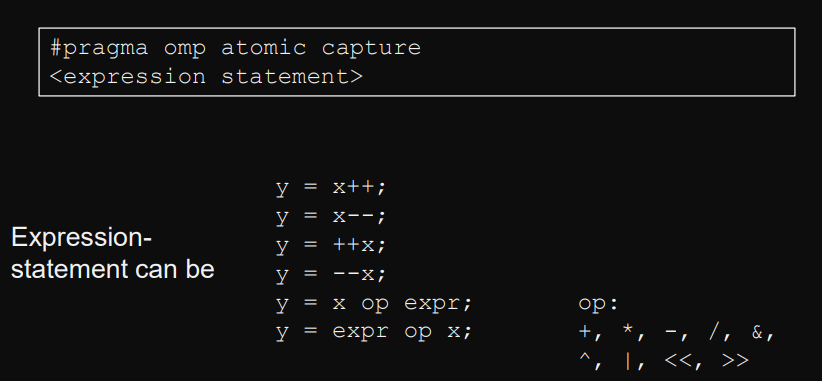
#pragma omp atomic [operation_type]Operations: Read, Write, Update, Capture (fetch and update)
#pragma omp atomic read pvar = svar; // read shared variable atomically#pragma omp atomic write svar = pvar; // write to shared variable atomically#pragma omp atomic capture <expression statement>#pragma omp atomic capture <structured block>#pragma omp atomic update <expression statement>structured block- Read of shared variable
- Update with one of the built in operators of the OpenMP standard.
Example: Counting accesses
This solution is better than a critical section (see above).
int t = 0;#pragma omp parallel shared(t) #pragma atomic update t++; <-- possible race condition on increment #pragma omp barrier print("Threads so far %d of %d by %d\n", t, omp_get_num_threads(), omp_get_thread_num());int t, i; t = 0;#pragma omp parallel shared(t) private (i) #pragma atomic capture i = t++; <-- possible race condition on increment #pragma omp barrier print("Threads so far %d of %d by %d\n", i, omp_get_num_threads(), omp_get_thread_num());
Performance
Performance comparison
Critical section, lock
Slow - causes overhead for locking/mutual exclusion.
Can lead to serialization if too many threads must wait (amdahl).
Atomic operation
Usually much faster than critical sections, threads dont affect eachother’s progress if supported by hardware.
Possibly slow because of expensive traffic on memory system (if hardware must invalidate cache lines).
Loop schedule clauses (of for-construct)
Clauses used for scheduling in for-construct .
Loop scheduling
Assigning loop iterations (ie. indices of array) to threads.
By default:
= number of threads
= number of iterations (iteration space)
= chunk, block size (assigned to each thread)
the th chunk is:
The schedule (chunk size, assignment of chunks to threads) can be set via schedule clauses.
Schedule can have huge impact on performance (false sharing, work per iteration, data structure access pattern, ...)
Schedule clauses
#pragma omp parallel for schedule(…,<chunksize>)
for (j=0; j<n; j++) {
...
}schedule(static[, chunksize])- static, fixed assignment
chunksize argument is optional (default:)
Usingchunksize = 1would cause false sharing
Like round robin: thread executes chunk
Example: Matrix-vector multiplication
Default loop schedule is static with chunks.
#pragma parallel for for (i=0; i<n; i++) { y[i] = 0;for (j=0;j<m; j++) { y[i] += x[i][j]*A[j]; } }If written out explicitly:
#pragma parallel for schedule(static) for (i=0; i<n; i++) { y[i] = 0; for (j=0;j<m; j++) { y[i] += x[i][j]*A[j]; } }
schedule(dynamic[, chunksize])- dynamic assignment
chunksize argument is optional (default: 1)
assignment as threads become free and request work
can be implemented as work-pool
Thread where :
iis the chunk iteration startdo { start = fetch_and_add(&i, chunksize); // atomic instruction if (start>=n) break; end = min(start+chunksize,n);for (j = start; j<end; j++) { // execute chunk }} while (1);
schedule(guided[, chunksize])- guided assignment
chunksize argument is optional (default: 1)
same dynamic assignment, but chunksize is dynamic aswell:
possibly better load balance
Idea: if iterations are still left when thread grabs next chunk, then the best chunk size if all threads at that point would take a chunk would be .
schedule(auto)- automatic assignment
schedule chosen by compiler or on runtime
schedule(runtime)- assignment on runtime
schedule chosen by runtime and environment
Performance of clauses
Performance
Assume large , smaller :
If
chunksize
small → scheduling overhead
threads must handle >1 chunks:
- smaller overhead for static schedule: only div and mod operations
- larger overhead for dynamic and guided schedule: atomic operation or worse
If
chunksize
large → load imbalance
some chunks have significantly more work than others
Conculsion
reminder: a chunk consists of multiple iterations
-
equal work per chunk → static schedule
unequal work per chunk → dynamic, guided schedule
-
equal work per iteration → large chunksize
unequal work per iteration → small chunksize
Example: loop with condition
#pragma parallel for <schedule> for (i=0; i<n; i++) { if (condition(i,b,c)) a[i] = f(a[i],b[i]); }condition()holds oftenloop has high spatial locality.
static schedule.
chunksizeshould be a multiple of the cache-line size to avoid false sharing.
condition()holds rarely and inpredictablydynamic, guided schedule.
chunksizeshould be small.
Loop carried dependencies
Correctness, Independence (principle of OpenMP)
It is assumed that parallel regions contain code that can be safely executed in parallel and is independent .
Some special types of dependencies are supported by OpenMP (reduction pattern).
Compiler and runtime can not check everything.
- Safety no concurrent updates to shared variables
-
Independence update to shared variable in region can’t effect other regions
(no race conditions)
Loop carried dependencies
Loops are parallelizable if iterations are independent (has to be checked by programmer) :
- Array updates only
- Each element updated in ≤ 1 iteration
- Iterations dont read elements assigned by another iteration
Some types of dependencies can be resolved, some must be avoided with different algorithms (ie. flow dependency).
Example: Dependency within in same iteration (allowed)
#pragma omp parallel for for (i=0; i<n; i++) { a[i] = f(i); b[i] = g(i); c[i] = a[i]+b[i]; // dependency }#pragma omp parallel for nowait for (i=0; i<n; i++) a[i] = f(i); #pragma omp parallel for for (i=0; i<n; i++) b[i] = g(i); // implicit barrier (so a and b have correct values) #pragma omp parallel for for (i=0; i<n; i++) c[i] = a[i]+b[i]; // implicit barrier
Example: Loop carried dependencies (can be resolved)
for (i=0; i<n-k; i++) { a[i] = a[i] + a[i+k]; }Eliminated with temporary variables
#pragma omp parallel for firstprivate(k) for (i=0; i<n-k; i++) { aa[i] = a[i] + a[i+k]; // stored in temporary array } // swap a, aa (when finished) tmp = a; a = aa; aa = tmp;
Reduction pattern
Reduction pattern
global reduction variable referenced in each iteration to perform an associative operation.
Can cause data races (because we access the shared variable).
for (i=k; i<n; i++) sum = sum+a[i];Can be handled in 4 different ways:
Parallel thinking : Reduction clause (good performance)
#pragma omp parallel for reduction(+,sum) for (i=k; i<n; i++) sum = sum+a[i];
Sequential thinking : Ordered clause (bad performance)
Probably close to sequential loop but also has overhead.
#pragma omp parallel for ordered for (i=k; i<n; i++) { #pragma omp ordered sum = sum+a[i]; }
Concurrent thinking : Critical section (or dynamic locks)
Could have reasonable performance if work in parallel region would be significantly larger.
Correct only if operator + is commutative.
#pragma omp parallel for for (i=k; i<n; i++) { #pragma omp critical sum = sum+a[i]; }
Delegating to hardware : Atomic operations
Correct only if operator + is commutative.
#pragma omp parallel for for (i=k; i<n; i++) { #pragma omp atomic update sum = sum+a[i]; }
Other clauses
List of clauses used in different constructs.
lastprivate(a)
Stores value of
a
from last iteration back to pointer.
Example: getting last value
int t; // global#pragma omp parallel for lastprivate(t) // private copies of t for (i=0; i<n; i++) { if (event(i)) t = i; else t = -1; } // now t is index of last event or -1
collapse
Collapses nested loops
Example: Initializing matrix
for (i=0; i<n; i++) { for (j=0; j<m; j++) { x[i][j] = f(i,j); // thread safe but time depends on i, j } }Choosing which loop should be the inner or outer loop depends on:
- size of larger should be outer loop
- work of
#pragma omp parallel for collapse(2) for (i=0; i<n; i++) { for (j=0; j<m; j++) { x[i][j] = f(i,j); // thread safe but time depends on i, j } }Using clause to collapse nested loops:
Two loops are handled as one with iteration space
Transformation of compiler
#pragma omp parallel for for (ij=0; ij<n*m; ij++) { i = ij/m; j = ij%m; x[i][j] = f(i,j); }
Schedule is then easier to find.
reduction
reduction(<operator>:<variable list>)
Example: Sum
for (i=0; i<n; i++) sum = sum+a[i];sum = 0;#pragma omp parallel for reduction(+: sum) for (i=0; i<n; i++) sum = sum+a[i];
Example: Sum with conditional
#pragma omp parallel shared(a) private(i) { #pragma omp master a = 0;#pragma omp barrier // To avoid race condition #pragma omp for reduction(+:a) for (i = 0; i<100; i++) { if (i%2==0) a += i; } #pragma omp single printf ("Sum is %d\n", a); }
Example: All possible operations
Possible operators:
+,*,-,&,|,^,&&,||,min,maxint i, b, c; float a, d; a = 0.0; b = 0; c = y[0]; d = x[0];#pragma omp parallel for private(i) shared(x, y, n) \ reduction(+:a) reduction(^:b) \ reduction(min:c) reduction(max:d) for (i=0; i<n; i++) { a += x[i]; b ^= y[i]; if (c > y[i]) c = y[i]; // min/max expression d = fmaxf(d,x[i]); // min/max }
depend(used fortaskconstruct)
Define dependencies for tasks.
Changes order in which they are executed in DAG.
Tasks get deferred until dependencies are satisfied
depend(in: x,y,z)
task depends on tasks that return x,y,z
depend(out: x,z)
tasks that take x,z as arguments depend on this task
depend(inout: y)
task depends on tasks that return y or take it as their argument
priority(used fortaskconstruct)
Define priority for tasks (with integer)
Changes order in which they are executed in DAG (no guarantee - just a hint for runtime).
ordered(try to avoid)
Used to resolve loop carried dependencies by requiring a region to be iterated in sequential order .
Most likely results in no parallelization (slow down through serialization).
Example: Find primes
Sequential implementaion - Sieve-of-Erathostenes :
Finds all primes by crossing out multiples of each newly found prime.
Return found primes in increasing order in
primearray.called “pseudo polynomial”
for (i=2; i<n; i++) { mark[i] = true; // all prime? }for (i=2; i*i<n; i++) { // i<√n if (mark[i]) { // primefor (j=i*i; j<n; j+=i) { mark[j] = false; // not } } }k = 0; // collect those still marked for (i=2; i<n; i++) { if (mark[i]) prime[k++] = i; }Parallel implementation:
We can’t just parallelize all loops - there is a dependency in the last loop.
ILLEGAL: Each thread increments the shared variable
k.#pragma omp parallel for for (i=2; i<n; i++) mark[i] = true;for (i=2; i*i<n; i++) { if (mark[i]) {#pragma omp parallel for for (j=i*i; j<n; j+=i) { mark[j] = false; } } }k = 0; #pragma omp parallel for for (i=2; i<n; i++) { if (mark[i]) prime[k++] = i; // <-- ILLEGAL }Possible solutions:
Removing the parallel for-construct altogether.
Enforcing sequential order in parallel region with
order(inefficient)#pragma omp parallel for for (i=2; i<n; i++) mark[i] = true;for (i=2; i*i<n; i++) { if (mark[i]) {#pragma omp parallel for for (j=i*i; j<n; j+=i) { mark[j] = false; } } }k = 0; #pragma omp parallel for ordered for (i=2; i<n; i++) { #pragma omp ordered if (mark[i]) prime[k++] = i; }
Index computation in parallel = Array compaction (efficient)
#pragma omp parallel for for (i=2; i<n; i++) mark[i] = true;for (i=2; i*i<n; i++) { if (mark[i]) {#pragma omp parallel for for (j=i*i; j<n; j+=i) { mark[j] = false; } } }// array compaction k = 0; kix[0] = 0; kix[1] = 0; #pragma omp parallel for for (i=2; i<n; i++) { kix[i] = (mark[i]) ? 1 : 0; } Exscan(kix,n); // exclusive prefix-sums#pragma omp parallel for for (i=2; i<n; i++) { if (mark[i]) prime[kix[i]] = i; }