Parallel patterns
Design pattern / Programming pattern / Skeleton
General reusable solution to commonly recurring problems in software design / algorithm design.
Parallel patterns
Design patterns with good parallel implementations.
“Automatic parallelization” won’t work because the concepts in the parallel solutions are not always found in the sequential solutions.
Parallelization is problem and architecture dependent. There is no general strategy for parallelizing an algorithm.
Memory model
= When do data written by one processor become “visible” to other processors?
Different memory models for each implementation:
Shared memory programming model
implicit and explicit synchronization
UMA vs. NUMA - memory cost model and access time
Distributed memory programming model
Assumption: Data is distributed to processors in blocks before the processes start locally.
Cost of redistribution, communication, synchronization
Not all problems can be parallelized.
ie. Graph search problems (DFS, BFS, ...) are extremely difficult to parallelize:
Methodology to parallelize computations:“4 steps of Foster”
- Partitioning
Dividing computation into independent tasks
- Communication
Determining communication between tasks
- Agglomeration/aggregation
Combining tasks, communication to larger independent “chunks”
- Mapping
Assigning tasks, communication to processes, threads, ...
Data distribution
Data distributions (in parallel programming models)
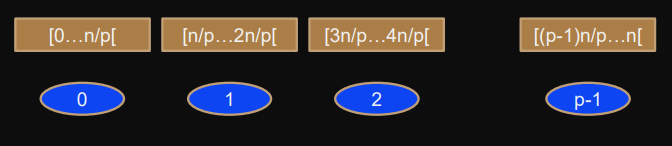
block-wise block
j
contains elements
[jn/p, jn/p+1, ..., 2jnp-1]
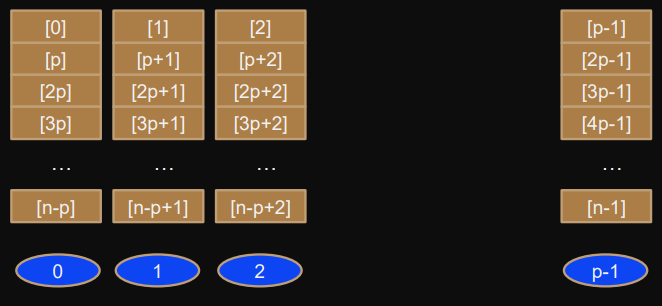
cyclic round-robin distribution: element
i
is in block
i%p
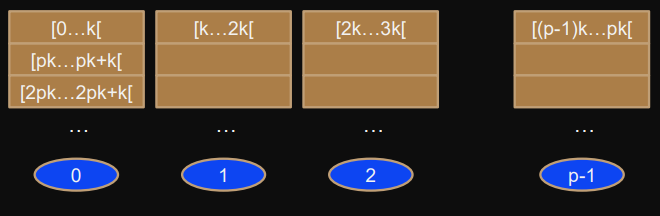
block-cyclic blocks of size
k
distributed cyclically
irregular blocks of possibly different sizes → mapping global to block index
1) Block-wise
“Owner computes rule”: Block
j
associated with / owened by processor
j
.
Possibly better performance for NUMA and distributed memory systems (spatial locality).
2) Cyclic
Owner of element
i
can be determined in
time and space.
3) Block-cyclic
Round-robin distribution of blocks of
k
elements.
Owner of element
i
can be determined in
time and space.
4) Irregular
Owner of element
i
can be determined in
time and space with
sized array.
Otherwise compact data structure with fast lookup needed → then no longer .
(shown below for a single processor)
Loop
Loop patterns
par (0≤i<n) {
a[i] = F(i,n,…);
}Data parallelism / data parallel pattern
Same operation applied to multiple elements (in data structure)
Map
Same operation applied to sequence.
SIMD parallelism / SIMD pattern
Single instruction (flow F) controls operation on many elements (in data structure)
Gather/Scatter
Gather/Scatter pattern
- Gather
Collect elements of data structure into consecutive compact blocks.
Make input “denser” / more compact
- Scatter
Distribute elements of consecutive compact blocks into data structure.
Compute
- Reduce
(as in MapReduce) Combine result into single block.
Insert result into previous input structure
MapReduce
MapReduce pattern
Available data assigned to available processors
then reduced with reduction operation (here: sum).
for (i=0; i<n; i++) {
a[i] = F(i,n,…); // map
}
result = ∑ a[i]; // reduceExample: counting words in a document
- Distribute assign text parts to processors
- Map each processor creates own dictionary with (word, count) pairs
- Map each processors sorts dictionary lexicographically after words
- Reduce all dictionaries are merged, for each word, all counts added
(requires load balancing)
Stencil
Stencil pattern (one dimensional)
Goal: Iterating through array
Sequential: not data parallel, dependent iterations
for (i=0; i<n; i++) {
a[i] = a[i-1] + a[i] + a[i+1];
}Parallel: Removing dependencies with extra space
for (i=n[j]; i<n[j+1]; i++) {
tmp[i] =a[i-1]+a[i]+a[i+1];
}
barrier;
x = tmp; tmp = a; a = x; // swap (more efficient than copying)
Synchronization: Processor
needs access to
a[n[j]-1]
and
a[n[j+1]]
before they are updated by processors
and
.
General stencil pattern
Given:
-
data structure
ie. 2D matrix
-
update rule
ie. local neighborhood, template, stencil
mostly → total work for update
must have specification for borders
Pattern:
Update all elements using update rule.
Apply stencil on all elements .
Stencil pattern parellelization through domain decomposition
Domain decomposition:
Dividing evenly over available processors
each responsible for updates on its subdomains.
Can be shared or distributed memory.
Issues:
Borders of subdomains: writing into the subdomain of other processor.
communication / synchronization with neighboring processors needed
Keeping updates synchronized.
Load balancing.
Data driven parallelization
Data distribution
Data distribution decides how we parallelize: “perform computations where the data is”
Assumptions: locality matters because of NUMA model
Paritioned Global Address Space PGAS
- Divide date structures across processors (based on some distribution)
- “Owner computes”-rule
- If processor accesses data owned by other processor: (implicit) communication.
Needs efficient ownership.
Example: Owner computes, compiler translates loops
for (i=n[j]; i<n[j+1]; i++) {
a[i] = f(i);
}for (i=0; i<n; i++) {
if (owns(i,j)) a[i] = f(i);
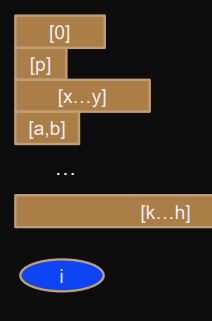
}Pipeline patten (MISD parallelism)
Linear pipeline (can be complex DAG)
Pipeline latency after steps a first output is produced
Pipeline throughput in each step, a new output block is produced - each step takes
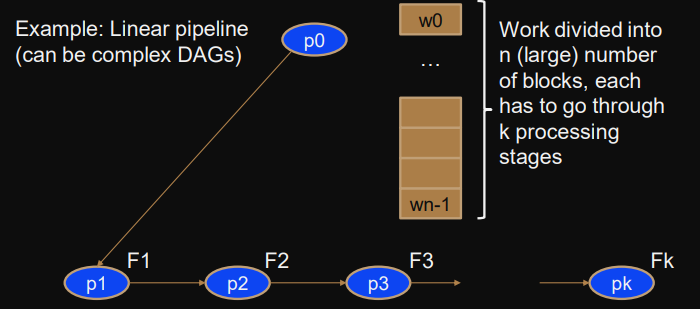
Master-worker (Asymmetric work-distribution)
Master-worker
Worker processor requests work from master - returns solution
Pattern can potentially keep all processors busy: .
Good if in subproblems work/size ratio is high and workers can compute asynchronously.
Master solves “Termination detection problem”: no more subproblems → terminate.
Master can be sequential bottleneck.
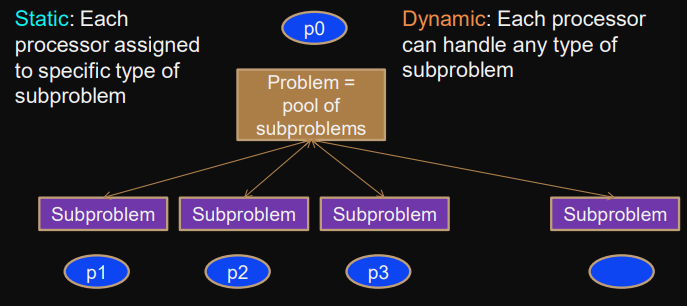
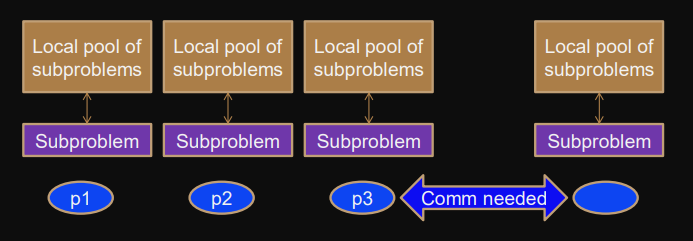
Load balancing: Master-worker variation
Work-pool is distributed and workers have local pools.
Communication between workers allowed:
- work-dealing overfull pools initiate redistribution
- work-stealing processors with empty work-pool steal/request from others
Problem: Termination detection gets difficult.