Prefix-sums, reduction
Collective opereation (pattern)
Reduction and prefix-sums are collective operations.
A set of processors cooperatively carrying out an operation on a data-set.
Other examples
Broadcast One processor has data that all the others receive
Scatter One processor has data that all the other’s receive in their blocks
Gather Blocks from all processors get collected by one processor
Allgather Blocks from all processors get collected by all processors
also called: broadcast-to-all
Alltoall Each processor collects block from other processor
Definition: Reduction
Reduction problem
Given sequence
elements can be: integers, real numbers, vectors, ...
and associative operation
has algebraic property:
compute
Examples: Reduction as collective operation
- Reduction-to-one
All processors participate. Result stored in “root”-processor.
- Reduction-to-all
All processors participate. Result available to all.
- Reduction-with-scatter
Using vectors. Result stored in blocks over the processors according to some rule.
- Reduction-to-one
Definition: Prefix-sums
Prefix sums problem
Given sequence compute all inclusive/exclusive prefix sums .
and there is a special definition for
Exclusive prefix sum, computed by process
(can’t be derived from inclusive sum unlesshas an inverse operation).
in
Inclusive prefix sum (including ), computed by process
(same as exclusive prefix sum +)
Theorem: Speedup is at most
For computing the prefix-sums of an input sequence, the following trade-off holds between:
size, number of operations
depth,
Sequential solution
Solution to both reduction and prefix sums problem.
This is the best possible, since output depends on.
Work total operations
Fastest possib. parallel
applications of
time complexity
implementation (not the best)
for (i=1; i<n; i++) { x[i] = x[i-1] + x[i]; } memory reads
summations
implementation - improved
1 read, 1 write per iteration
optimizer in compiler can improve performance significantly
register int sum = x[0]; // compiler stores in register for faster access for (i=1; i<n; i++) { sum += x[i]; // read x[i] = sum; // write }
Parallel solution (intuitively)
Solution to both reduction and prefix sums problem.
What we ideally want:
Work
Fastest poss. parallel
applications of close to
time complexity for large range of
In most architecturesis reasonable for a work-optimal solution.
We want to make use of the associativity of the operator:
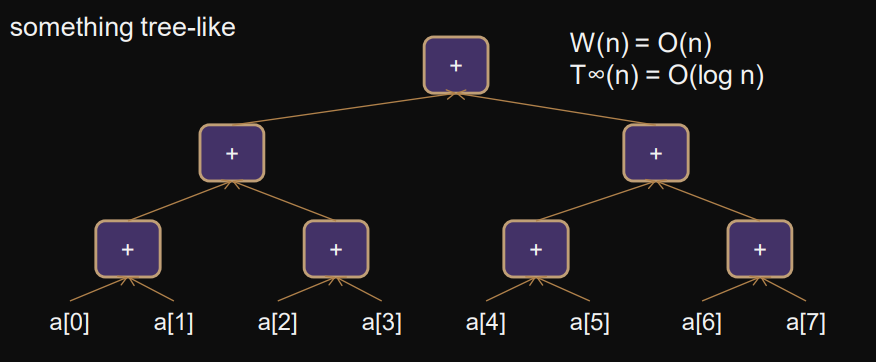
There are 3 parallel solutions to inclusive prefix sums:
- recursive fast, work-optimal
- iterative fast, work-optimal
- doubling faster, not work-optimal but still useful
List ranking (= Generalization of prefix-sums problem)
Generalization of prefix-sums problem:
Given list compute all list-prefix sums.
Find list head and follow the pointers and sum up: .
Not solvable with blocking technique.
List stored in array but indices have no relation to position in list.
Index of first and last element (head and tail) may not be known.
can be solved in parallel in parallel time steps.
1) Recursive
Recursive solution
Sum pairwise, then recurse on smaller problems.
Scan(x,n) {
if (n==1) {
return;
}for (i=0; i<n/2; i++) {
y[i] = x[2*i] + x[2*i+1];
}// solve recursively in y -> implicit (with fork-join) or explicit barrier
Scan(y,n/2);// take back
x[1] = y[0];
for (i=1; i<n/2; i++) {
x[2*i] = y[i-1] + x[2*i];
x[2*i+1] = y[i];
}if (odd(n)) {
x[n-1] = y[n/2-1] + x[n-1];
}
}Example
for (i: 0 --> 3) { y[i] = x[2*i] + x[2*i+1]; } x = [1, 2, 1, 4, 3, 2, 3, 6] n = 8 \__/ \__/ \__/ \__/ 3 5 5 9 y = [3, 5, 5, 9]Scan(y,n/2); y = [3, 8, 13, 22]x[1] = y[0]; x = [1, 3, 1, 4, 3, 2, 3, 6]for (i: 1 --> 3) { x[2i] = y[i-1] + x[2i]; x = [1, 3, 4, 4, 11, 2, 16, 6]x[2i+1] = y[i]; x = [1, 3, 4, 8, 11, 13, 16, 22] }
Number of operations, recursive calls
All for loops are data parallel → perfectly parallelizable:
Work of each for-loop:
Time of each for-loop:
Total number of operations of operations :
(geometric series)
Number of recursive calls which will be satisfies:
Proof
Correctness (proof through induction)
Claim:
Algorithm computes the inclusive prefix sums of .
That means
is the value ofbefore the call
Proof by induction:
Base is correct: The algorithm does nothing and just returns.
Pairing:
Then calling
Scan(y,n/2).Therefore:
odd
even
Summary
Work
Time
Parallelism processors
Parallel steps parallel steps (recursive calls)
2 synchronizations per recursive call
operations
Advantages
- Smaller array might fit in cache
- pair-wise summing has good spatial locality
Drawbacks
- space: extra sized array in each recursive call ( in total)
- About operations of (compared to sequential:)
- parallel steps
2) Iterative
Eliminates recursion and extra space.
Can only compute sum for arrays with elements where
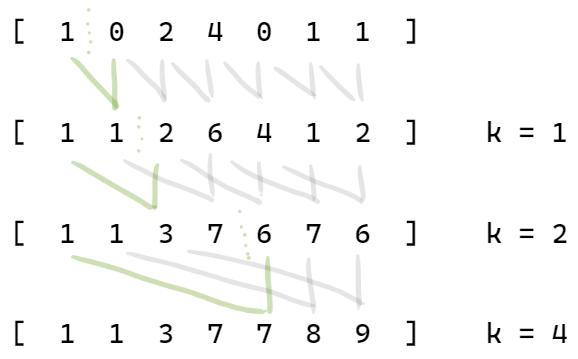
in rounds:
In round , the operation is done for every th element.
This way:
Lemma
Reduction can be performed out in synchronized rounds for (if it’s a power of two).
Total number of operations are
Geometric series
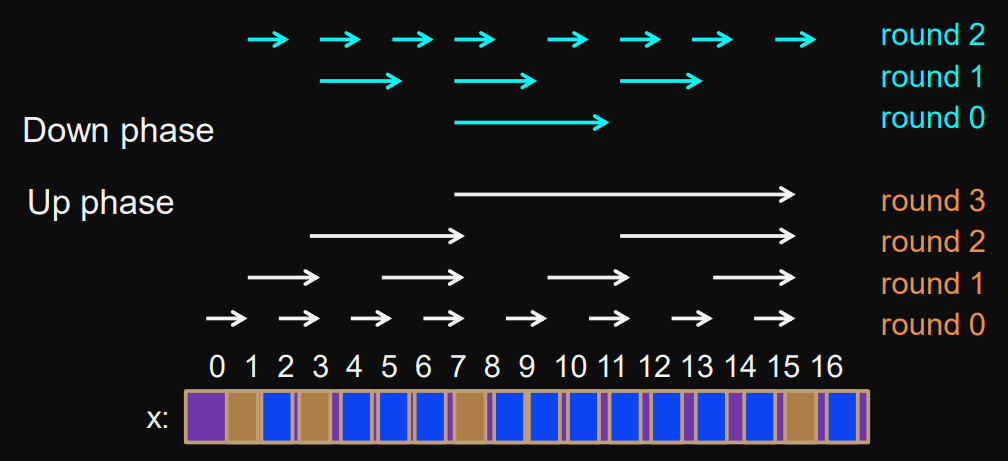
Iterative solution
for (k=1; k<n; k=kk) {
kk = k<<1; // double
par (i=kk-1; i<n, i+=kk) {
x[i] = x[i] + x[i-k];
}barrier;
}for (k=1; k<n; k=kk) {
kk = k<<1; // halve
par (i=kk-1; i<n, i+=kk) {
x[i] = x[i] + x[i-k];
}barrier;
}
Parallelization of inner loop
The inner for-loop can be parallelized (not the outer one).
This way we can get from operations in each round to .
Total work
Factor is off from sequential work.
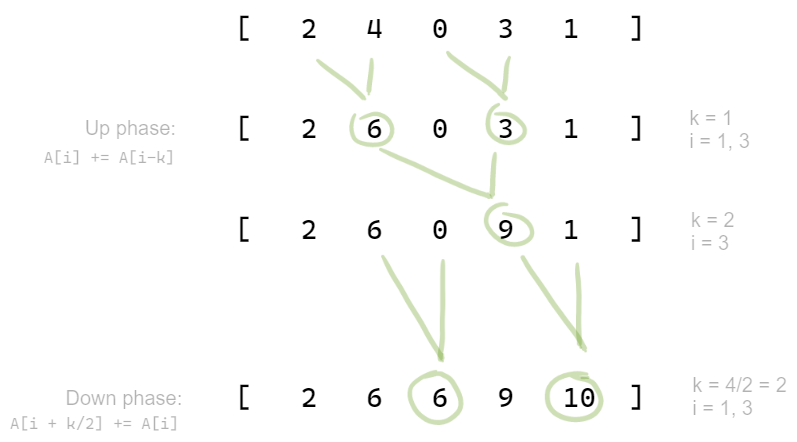
Invariants
Invariant for Up-Phase
Invariant for Down-Phase
Distributed programming models
Synchronization can get very expensive for largerelative toin in distributed memory models.
communication rounds each with concurrent communication operations.
operations in total.
Since often this is too expensive.
Summary
Work
Time rounds each =
Linear speedup - half the processors are lost
operations about
Advantages
- In-place (extra space required: input and output are the same array)
- Work-optimal, simple, parallelizable loops
- No recursive overhead
Disadvantages
- Less cache-friendly than recursive solution - less spacial locality with increasing step-size.
- rounds
- About operations with
3) Doubling
Faster butnot work optimalsolution.
In each round every processor computes: we are not using every th processor as in the previous solution.
Invariance
Round
with rounds needed in total.
int *y = (int)malloc(n*sizeof(int));
int *t;for (k=1; k<n; k=k*2) {
par (i=0; i<k; i++) y[i] = x[i]; // skip first elements
par (i=k; i<n; i++) y[i] = x[i-k]+x[i]; // add
barrier;
t = x; x = y; y = t; // swap x, y
}Invariant
Before each iteration of step :
Summary
Advantages
- Only rounds (and synchronization / communication steps)
- Simple parallelizable loops
- no recursive overheads
Drawbacks
- not work-optimal
- less spatial locality, less cache friendly with increasing step-size
- Extra array of size needed to eliminate dependencies