Work as a DAG

Work

Work to solve problem $\small P$ with input of size $\small n$ :

can be described as set of smaller tasks

executed in some order, constrained by dependencies.

Work

$\small \text{Wseq}(n) = \text{Tseq}(n)$ total number of executed instructions

$\small W(n)$ or $\small \text{Wpar}(n) = \sum_{0\leq i <p} T_i(n)$ by all processors (not including idle / waiting times)

$\small \text{Wpar}(n)= \sum_{0 \leq i < k} \text{W}_i(n) \geq \text{Tseq}(n)$

$\color{pink}\small \text{Wpar}(n) \geq \text{Tseq}(n)$

If this isnotthe case there must be a better algorithm than $\small \text{Tseq}(n)$ → contradiction.

Work optimality

$\small \text{Wpar}(p,n) \in O(\text{Wseq}(n) )$

Should be the case here.

Fastest running time / fastest possible parallel

$\small T_\infin(n)$

= smallest possible running-time of $\small \text{Par}$ with arbitrarily many processors

= smallest number of parallel steps in which work can be done is

Work-time relationship of parallel algorithms

Work should be work-optimal

Assuming that load balanced and work assigned evenly to processors:

$\color{pink}\small \text{Tpar}(p,n) \in O(\text{Wpar}(p,n)/p + T_\infin(n))$

Work as DAG (Directed Acyclic Graph)

Computation can be structured as tree / directed acyclic graph DAG.

Example: Quicksort
```
void QuickSort(int x[], int n) {
if (n<=1) return;pivot = pivot(x,n); // x[pivot] as pivot value
ix = partition(x,n,pivot); // partition, return new pivot index
QuickSort(x,ix); // sort elements until pivot
QuickSort(x+ix+1,n-1-ix); // sort elements after pivot
}
```
pivot(n) $\small O(1)$
partition(n) partition into elements smaller, equal, larger than pivot in $\small O(n)$
Recursion depth in best case $\small (\log_2n)$ .
Total work $\small O(n \log n)$ .
💡
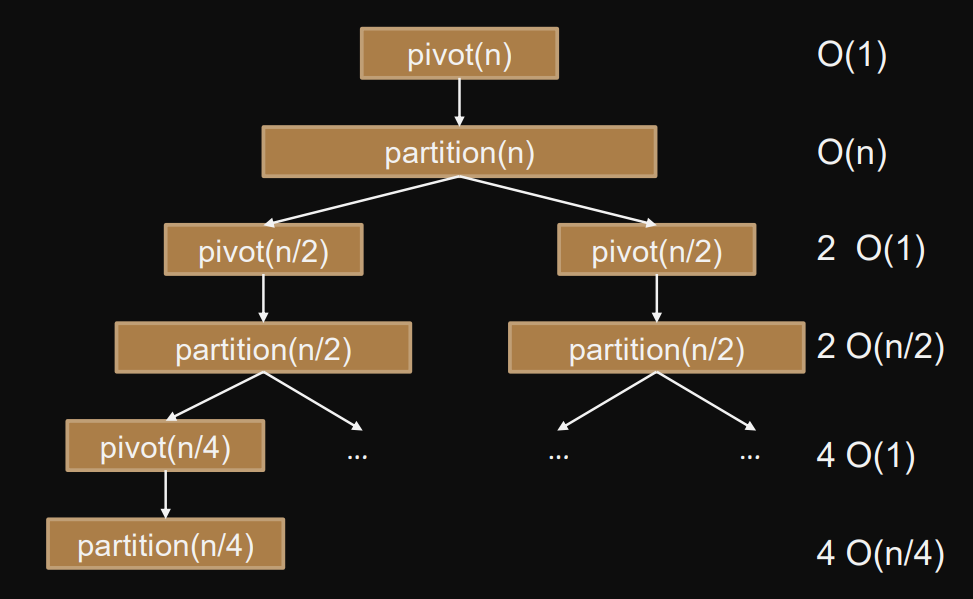Every single node must be executed in order for problem to be solved (not just a path from root to leaf)

Task $\small t_i$

a sequential computation (strand)

requires input data (from other tasks) - or else can not be executed

produces output data (to other tasks)

Work as DAG

Work shown with directed acyclic graph $\small G= (V,E)$

$\small V$ vertices, task set $\small \{t_1, t_2, \dots, t_n \}$

root called start node

leaf called final node

nodes without ancestors called ready nodes

$\small E$ data dependencies $\small t_i \rarr t_j$

means that $\small t_i$ can’t be executed before $\small t_j$ has completed (dependency).

transfering output of one task to the input of another called communication cost .

$\small t_j$ is dependent from $\small t_i$ if there is a path from $\small t_i$ to $\small t_j$ .

Node task $\small t_i$ / strand / work package

Input nodes no incoming edges

Output nodes no outgoing edges

Dependence when $\small \exists$ path between two tasks

Parallel execution Tasks scheduled to processors with respect to dependencies

$\small \text{Tp}(n)$ or $\small \text{Tpar}(p,n)$ Time for $\small p$ processors with given schedule

$\small W_i(n)$ Work of $\small t_i$ : number of sequential operations

$\small \text{W}(n)= \sum_{0 \leq i < k} \text{W}_i(n)$ total work, sum of nodes (ignoring communication costs)

Depth / Span / Fastest possible parallel

Execution with unlimited number of processors.

Number of operation in heaviest path from input to output node:

$\small T_\infin(n) = \sum_{i \in \text{heaviest path}}W_i(n)$

in a good DAG, it shouldn’t be a constant fraction of $\small W(n)$

Therefore:

$\small \text{Tpar}(p,n) \geq T_\infin(n)$

Lower bounds

Work law $\small \text{Tpar}(p,n) \geq \text{Wpar}(n)/p \geq \text{Tseq}(n)/p$

Depth law $\small \text{Tpar}(p,n) \geq T_\infin(n)$

Max speedup $\small \text{Wpar}(n)/ T_\infin(n)$ - also called paralellism

$\small S_p(n) = \text{Tseq}(n)/\text{Tpar}(p,n) ≤ \text{Tseq}(n)/T_∞(n) ≤ \text{Wpar}(n)/T_∞(n)$

Independence

when there is no path from $\small t_i$ to $\small t_j$ and vice versa.

can be executed in parallel.

Execution (= topological order)

Repeat until all tasks are executed:

Pick a task that is ready (no incoming edges / dependencies)

Execute task by some processor

Remove edges to all its children (successor tasks become available “ready nodes”)
“Ready nodes” can be executed on available processors.

Remove task

Best possible execution time

$\small \text{W}(n)/ p$

therefore $\small \text{Tpar}(p,n) \geq \text{Wpar}(n)/p \geq \text{Tseq}(n)/p$

DAG Design guidelines

“work-depth analysis” gives more informative upper-bounds on speedups than naive Amdahls’ law:

Look at “critical path” instead of just “sequential fraction”.
Design for light critical path $\small T_\infin$ compared to total work $\small W$ .

Find ways to specify good DAGs by:
$\small \text{Wpar} = \text{Tseq}$
using small $\small T_\infin$

Find efficient way to schedule DAG nodes:
num of parallel steps $\small \approx \max(W(n)/p,~T_\infin)$

Scheduling Work-DAGs

Scheduling

= Finding ready task $\small t_i$ to assign to a processor $\small k \in [0;~p-1]$ at start time $\small s_j$ .

respect dependencies don’t start tasks predecessors have been completed

respect processors only assign one task to a processor at a time

Scheduling problem (NP-Hard)

finding the optimal schedule for some optimization criteria

ie. minimum completion time of last task

Scheduling on a single processor

Execute in topological order

Special cases

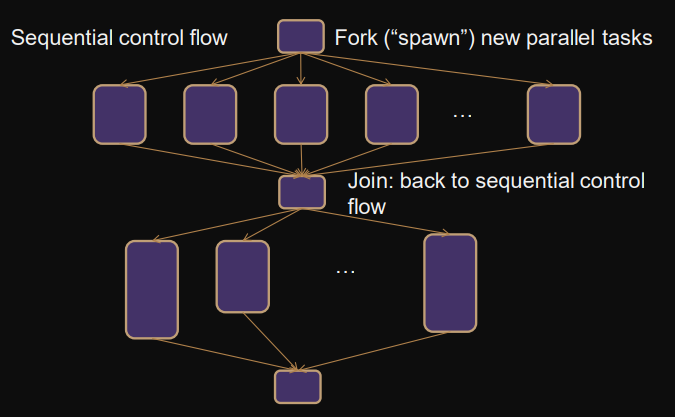
Fork-join parallelism (OpenMP programming model)

sequential control flow

fork spawning new parallel tasks

join joining back to sequential control flow

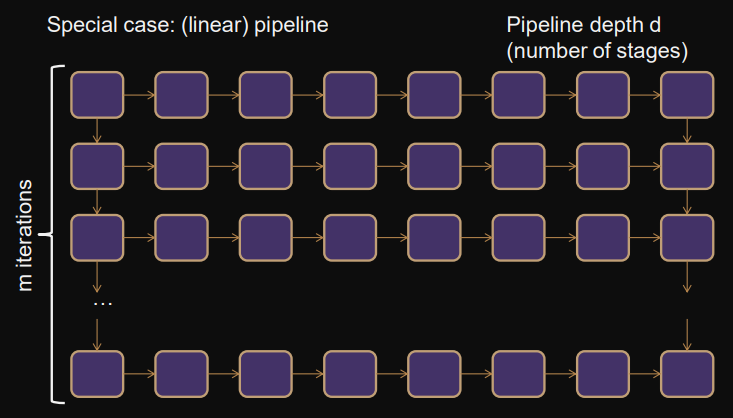
Linear pipeline

$\small d$ pipeline depth (number of stages)

$\small m$ iterations

Greedy DAG scheduling

Greedy DAG scheduler

Goal = Assigning as many tasks as possible to available processors.

“Complete step” = at least $\small p$ tasks are ready or being executed (otherwise called incomplete ).

Theorem

Greedy DAG scheduler executes with work $\small W$ and depth $\small T_\infin$ in:

$\small \text{Tpar}(p,n) \leq W / p + T_\infin$ time steps

Based on the other laws:

$\small \text{Tpar}(p,n) \leq W / p + T_\infin \leq 2 \cdot \max(W / p, T_\infin )$

Work law: $\small \text{Tpar}(p,n) \geq W/n$

Depth law: $\small \text{Tpar}(p,n) \geq T_\infin(n)$

Achieved $\small \text{Tpar}(p,n)$ is therefore usually within a factor of $\small 2$ from the optimal schedule (with minimal time as optimization criteria).