XQuery
Definition
XQuery
XPath XQuery
language for querying XML (and sorting and structuring query results)
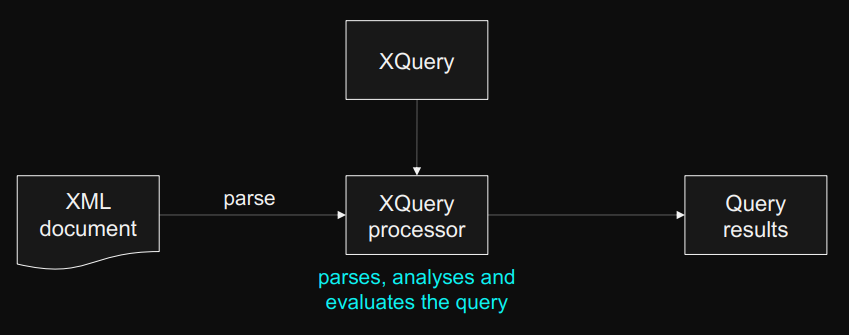
XQuery Processor
parsing getting semantics of text
analyzing static errors: searching syntax (independent of document), ...
evaluation dynamic errors: missing input document, division by zero, ...
Examples of usage
<courses> <course semester="Summer"> <title> SSD </title> <day> Thursday </day> <time> 09:15 </time> <location> HS8 </location> </course> <course semester="Winter"> <title> Databases </title> <day> Tuesday </day> <time> 09:15 </time> <location> HS8 </location> </course> </courses>Query:
doc("courses.xml")/courses/course/title<title> Semi-structured Data </title> <title> Databases </title>Query:
doc("courses.xml")/courses/course[@semester="Winter"]/titleQuery:
for $x in doc("courses.xml")/courses/coursewhere $x/@semester="Winter"return $x/title<title> Databases </title>Query:
for $x in doc("courses.xml")/courses/coursewhere $x/@semester="Winter"order by $x/title descendingreturn $x/title<title> SSD </title> <title> Databases </title>
FLWOR Expressions
FLWOR
pronounced: “flower expressions”
generalized version of
select from having where
in SQL
F
for
L
let
W
where
O
order by
R
return
Example of FLWOR
for $d in doc("departments.xml")//dept_no let $e := doc("employees.xml")//employee[dept_no = $d] where count($e) >= 10 order by avg($e/salary) descending return <large_dept> {$d} <size> {count($e)} </size> <avg_salary> {avg($e/salary)} </avg_salary> </large_dept>forgenerates bindings ofdept_novalues to$d
letgenerates another binding to$e: employees withdept_noas$d→
forandletcan be used multiple times
wherefilters that list to keep only the desired pairs (at least 10 employees)
order bysorts that lists by the given criteria (sorted desceding by average salary)
returnconstructs for each pair a resulting value
Element Constructors
One can create new elements and add them in the result, by wrapping query into elements.
Example of Element Constructor
Here we create an element and attribute.
<sorted_departments> { for $d in doc("departments.xml")//dept_no let $e := doc("employees.xml")//employee[dept_no = $d] where count($e) >= 10 order by avg($e/salary) descending return <large_dept name = "{$d}"> {$d} <size> {count($e)} </size> <avg_salary> {avg($e/salary)} </avg_salary> </large_dept> } </sorted_departments>
Other Features
List
XQuery expressions manupulate lists of items.
operators
"3 to 10",union,intersect,except,concatenation with ","
functions
count,avg,max,min,sum,distinct-values, …
Conditional
if-then-else
expressions
(
else
is required but can be left empty with
()
)
Quantified Expressions
exists, forall expressed with
some ... in ... satisfies
every ... in ... satisfies