Automaten

💡
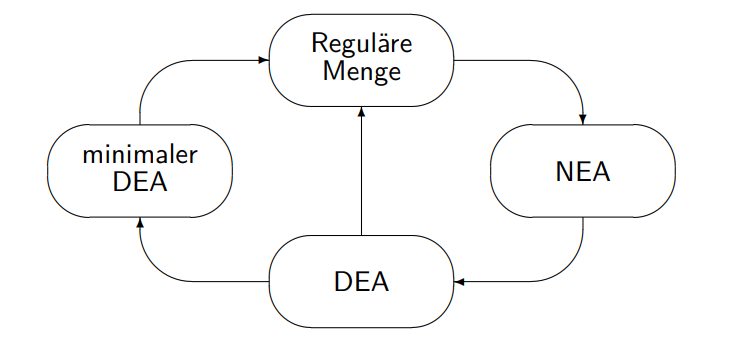
Zu jedem NEA gibt es einen äquivalenten DEA. (durch Determinisierung)

Endliche Automaten

Deterministischer Endlicher Automat DEA

A=(Q,Σ,δ,q0,F)\mathcal{A}=\left(Q, \Sigma, \delta, q_{0}, F\right)

Übergangsfunktion

δ:Q×Σ→Q\delta: Q \times \Sigma \rightarrow Q

Erweiterte Übergangsfunktion

δ∗:Q×Σ∗→Q\delta^{*}: Q \times \Sigma^{*} \rightarrow Q(wobeiΣ∗\Sigma ^*ein Wortwwist)

δ∗(q,ε)=q\delta^{*}(q, \varepsilon)=q

δ∗(q,aw)=δ∗(δ(q,a),w)\delta^{*}(q, a w)=\delta^{*}(\delta(q, a), w)

Akzeptierte Sprache

L(A)={w∈Σ∗∣δ∗(q0,w)∈F} \mathcal{L}(\mathcal{A})=\left\{w \in \Sigma^{*} \mid \delta^{*}\left(q_{0}, w\right) \in F\right\} 

Nicht-Deterministischer Endlicher Automat NEA

Übergangsfunktion NEA

δ:Q×Σ→P(Q)\delta: Q \times \Sigma \rightarrow \mathcal{P}(Q)(Potenzmenge von Zuständen)

δ:Q×(Σ∪{ε})→P(Q) \delta: Q \times(\Sigma \cup\{\varepsilon\}) \rightarrow \mathcal{P}(Q) (fürε\varepsilon-NEA)

Erweiterte Übergangsfunktion

δ∗:Q×Σ∗→P(Q) \delta^{*}: Q \times \Sigma^{*} \rightarrow \mathcal{P}(Q) 

δ∗(q,w)={q′∈Q∣q⇝wq′} \delta^{*}(q, w)=\left\{q^{\prime} \in Q \mid q \rightsquigarrow w q^{\prime}\right\} (es gibt einen Pfad mitwwvonqqnachq′q')

Akzeptierte Sprache

L(A)={w∈Σ∗∣δ∗(q0,w)∩F≠{}} \mathcal{L}(\mathcal{A})=\left\{w \in \Sigma^{*} \mid \delta^{*}\left(q_{0}, w\right) \cap F \neq\{\}\right\} 

Äquivalenz vonA\mathcal AundA′\mathcal A'

L(A)=L(A′) \mathcal{L}(\mathcal{A})=\mathcal{L}\left(\mathcal{A}^{\prime}\right) 

Falle

q∈Q−Fq \in Q-Fwobei∀a∈Σ:δ(q,a)=q\forall a\in \Sigma : \delta(q, a)=q

Minimalautomat

Zu jeder regulären Sprache LL gibt es einen endlichen Automaten A\mathcal A , sodass L=L(A)L = L(\mathcal A) .

Reguläre Sprache ↦\mapsto eindeutiger DEA mit minimaler Anzahl an Zuständen.

Kann mit dem Minimierungsalgorithmus von Brozozowski erhalten werden.

Reversen Automat reversen →L(Ar)=Lr\small L(A^{r})=L^{r}

Ar=(Q,Σ,{(q,a,p)∣(p,a,q)∈δ},F,{q0}) A^{r}=\left(Q, \Sigma,\{(q, a, p) \mid(p, a, q) \in \delta\}, F,\left\{q_{0}\right\}\right)