Grammatiken

$G=\langle N, T, P, S\rangle$

$N$ Non-Terminale (Variablen)

$T$ Terminal-Symbole

$P \subseteq (N \cup T)^+ \times (N \cup T)^*$ Produktionen

Man schreibt $\small \alpha \rarr w$ statt $\small (\alpha,w) \in P$

$\small \alpha \rightarrow \beta_{1}|\cdots| \beta_{n}$ statt $\small \alpha \rightarrow \beta_{1}, \ldots, \alpha \rightarrow \beta_{n}$

$S \in N$ Startsymbol

Satzform

$w \in(N \cup T)^*$

Wenn $S \Rarr w$ , dann ist $w$ ein Satzform.

Die Menge aller in $n$ Schritten ableitbaren Satzformen:

$S F(G, n)=\left\{w \in(N \cup T)^{*} \mid S \Rightarrow^{n} w\right\}$

Erzeugte Sprache

$\mathcal{L}(G)=\left\{w \in T^{*} \mid S \Rightarrow^{*} w\right\}$

Zwei Grammatiken äquivalent wenn $\mathcal{L}\left(G_{1}\right)=\mathcal{L}\left(G_{2}\right)$

Kontextfreie Grammatiken

Kontextfrei bedeutet dass die Ableitungs-Art keine Rolle spielt und man immer die selbe Sprache erzeugt.

$\begin{aligned}\mathcal{L}(G) &=\left\{w \in T^{*} \mid S \Rightarrow^{*} w\right\} \\&=\left\{w \in T^{*} \mid S \Rightarrow_{\textcolor{pink}L}^{*} w\right\} \\&=\left\{w \in T^{*} \mid S \Rightarrow_{\textcolor{pink}R}^{*} w\right\} \\&=\left\{w \in T^{*} \mid S \Rightarrow_{\textcolor{pink}P}^{*} w\right\}\end{aligned}$

Kontextfreie Grammatiken sind

abgeschlossen unter

$\cup, \cdot,^{*}$
- Beispiel
  $G_{1}=\left\langle N_{1}, T_{1}, P_{1}, S_{1}\right\rangle, \quad G_{2}=\left\langle N_{2}, T_{2}, P_{2}, S_{2}\right\rangle$
  $N_{1} \cap N_{2}=\{\}$
  $S \notin N_{1} \cup N_{2}$
  Kontextfreie Grammatiken:
  $\begin{aligned}&G_{\text {union }}=\left\langle N_{1} \cup N_{2} \cup\{S\}, T_{1} \cup T_{2},\left\{S \rightarrow S_{1} \mid S_{2}\right\} \cup P_{1} \cup P_{2}, S\right\rangle \\&G_{c a t}=\left\langle N_{1} \cup N_{2} \cup\{S\}, T_{1} \cup T_{2},\left\{S \rightarrow S_{1} \cdot S_{2}\right\} \cup P_{1} \cup P_{2}, S\right\rangle \\&G_{\text {star }}=\left\langle N_{1} \cup\{S\}, T_{1},\left\{S \rightarrow \varepsilon, S \rightarrow S_{1} S\right\} \cup P_{1}, S\right\rangle\end{aligned}$

Homomorphismen

Durchschnitt $\cap$ mit regulären Sprachen

nicht abgeschlossen unter

Durschschnitt $\cap$
- Beispiel
  $L_{1}=\left\{a^{m} b^{m} c^{n} \mid m, n \geq 1\right\}$
  $L_{2}=\left\{a^{m} b^{n} c^{n} \mid m, n \geq 1\right\}$
  $L=L_{1} \cup L_{2}$
  $S \rightarrow S_{1} \mid S_{2}$
  $\begin{aligned}&S_{1} \rightarrow S_{1} c \mid A \\&A \rightarrow a A b \mid \varepsilon\end{aligned}$
  $\begin{aligned} &S_{2} \rightarrow \text { a } S_{2} \mid B \\ &B \rightarrow b B c\mid \varepsilon \end{aligned}$
  $L_{1} \cap L_{2}=\left\{a^{n} b^{n} c^{n} \mid n \geq 1\right\}$ → nicht kontextfrei
  Für jedes Wort aus dem Durchschnitt der beiden Sprachen kann man entweder über $S_1$ oder $S_2$ gehen.

Komplement
aus dem selben Grund wie beim Durchschnitt, da: $L_{1} \cap L_{2}=\overline{\overline{L_{1}} \cup \overline{L_{2}}}$

Ableitungsbäume

$G=(N, T, P, S)$

Wir erzeugen einen Ableitungsbaum $g=(K, E, L)$

über Knotenmarkierungen $U=N \cup T \cup\{\varepsilon\}$

und Kantenmarkierungen $W=\{1, \ldots, n\}$

für die gegebene kontextfreie Grammatik.

Es gilt:

$L(p_0) = S$

Wenn $p$ kein Blatt ist, muss $L(p)\in N$

Wenn $p$ ein Blatt ist, muss $L(p) = \varepsilon$

Die von $p$ wegführenden Kanten $\left\{\left(p, i, q_{i}\right) \mid i \in 1, \ldots, n\right\}$ erzeugen $L(p) = A$ wenn

$A \rightarrow L(q_{1}) \ldots L(q_{k})$ eine Produktion ist.

A-Baum

Wenn für die Wurzel gilt: $L(p_0) = A$ und $A \in N$

Ansonsten S-Baum.

Ordnungsrelation von Pfaden

Angenommen wir haben einen A-Baum.

Wir definieren eine Ordnungsrelation der Pfade:

$P(j)=\left(p_{j, 0}, e_{j, 1}, p_{j, 1}, \ldots, e_{j, k_{j}}, p_{j, k_{j}}\right)$

Angenommen wir haben 2 verschiedene Pfade von der Wurzel $j \in\{1,2\}$

$p_{1,0}=p_{2,0}=p_{0}$ (der 0te Knoten in Pfaden 1 und 2 ist $p_0$ )

dann definieren wir die Ordnungsrelation $P_1 < P_2$ wenn

$\exists m \geq 1$ sodass: $\forall 1 \leq i <m,~e_{1,m}<e_{2,m}:~ e_{1, i}=e_{2, i}$

(die Kanten von Pfade 1 und 2 sind überall gleich, außer in der Ebene $m$ , wo $P_1$ eine Kante mit einem niedrigeren Wert gewählt hat)

Front

Sind $p_1, \dots, p_k$ Blätter, dann ist die Front definiert durch $L(p_{1}) \ldots L(p_{k})$ .

Sätze

Sei $w \in(N \cup T)^{*}$ , dann gilt $A \Rightarrow^{*} w$ genau dann, wenn es einen A-Baum für die Grammatik mit $w$ an der Front gibt.

Sei $v\in T^*$ , dann gilt $S \Rightarrow^{*} v$ genau dann, wenn es einen Ableitungsbaum für die Grammatik mit $v$ an der Front gibt.

Jeder Linksableitung ( $\Rarr_L$ ) von einer Grammatik kann man eindeutig einen Ableitungsbaum zuordnen.
Wenn es zwei verschiedene Linksableitungen für dasselbe Wort gibt, dann sind die Ableitungsbäume nicht äquivalente Graphen.

Eindeutigkeit vs. Mehrdeutigkeit

Eindeutig vs. Mehrdeutig

Eindeutig wenn:

zu jedem ableitbaren Terminalwort es genau eine einzige Linksableitung gibt.

Ansonsten mehrdeutig.

Inhärent mehrdeutige Sprache

Mehrdeutig wenn:

jede Grammatik die Sprache $L$ erzeugt mehrdeutig ist (die Sprache nicht von einer eindeutigen Grammatik erzeugt werden kann).

Beispiel: Mehrdeutig

Mehrdeutige Grammatik zu der sich aber eine eindeutige Grammatik finden lässt

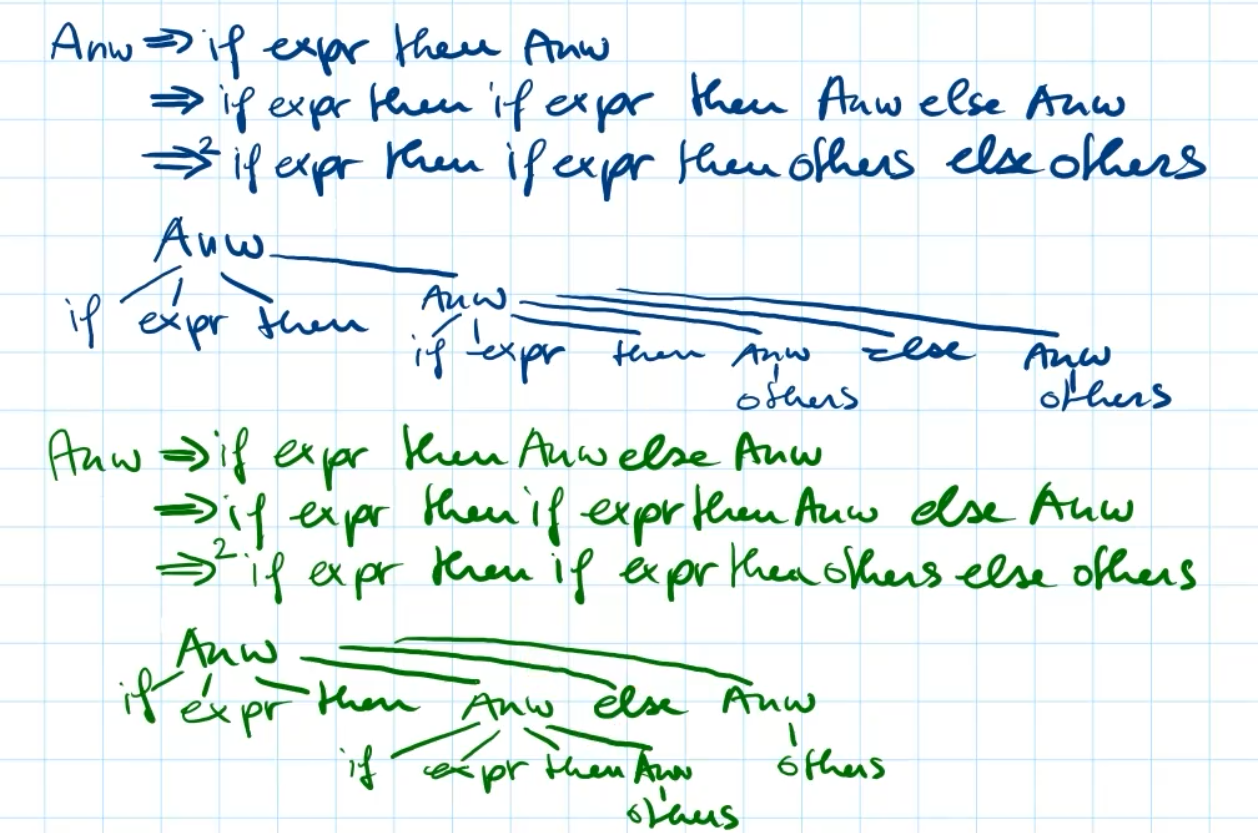
if-then-else Anweisung
$G_{1}=\left\langle\{A n w\},\{\text { if, then, else, expr, others }\}, P_{1}, \text { Anw }\right\rangle$
$\begin{aligned}&\text { Anw } \rightarrow \text { if expr then Anw } \\&\qquad\quad ~ \begin{array}{l}\text {| if expr then Anw else Anw } \\\text {| others }\end{array}\end{aligned}$
Das Wort $\small \color{grey} \text { if expr then if expr then others else others }$ besitzt 2 Linksableitungen:
Man kann in der Ableitung
$\text { if expr then \textcolor{red}{Anw }else \textcolor{red}{Anw} }$
entweder die linke oder rechte Anweisung nehmen.

Äquivalente eindeutige Grammatik
Es gibt keinen Algorithmus um alle mehrdeutigen Grammatiken eindeutig zu machen.
In diesem Fall wäre die eindeutige Version:
$\begin{aligned}G_{2}=&\langle\{\text { Anw, AnwT, AnwTE }\},\\&\left.\{\text { if, then, else, expr, others }\}, P_{2}, \text { Anw }\right\rangle\end{aligned}$
Hier lassen wir nur nach then eine Anweisung mit then-else zu.
$\begin{aligned} \text { Anw } & \rightarrow \text { AnwT } \\ & \mid \text { AnwTE } \\ \text { AnwT } & \rightarrow \text { if expr then } A n w \\ & \mid \text { if expr then AnwTE else AnwT } \\ \text { AnwTE } & \rightarrow \text { if expr then AnwTE else AnwTE } \\ & \mid \text { others } \end{aligned}$

Beispiel: Inhärent mehreutig

Mehrdeutige Grammatik zu der sich gar keine eindeutige Grammatik finden lässt

Vereinigung von 2 kontextfreien Grammatiken
$L_{1}=\left\{a^{m} b^{m} c^{n} \mid m, n \geq 1\right\}$
$L_{2}=\left\{a^{m} b^{n} c^{n} \mid m, n \geq 1\right\}$
$L=L_{1} \cup L_{2}$
$S \rightarrow S_{1} \mid S_{2}$
$\begin{aligned}&S_{1} \rightarrow S_{1} c \mid A \\&A \rightarrow a A b \mid \varepsilon\end{aligned}$
$\begin{aligned} &S_{2} \rightarrow \text { a } S_{2} \mid B \\ &B \rightarrow b B c\mid \varepsilon \end{aligned}$
$L_{1} \cap L_{2}=\left\{a^{n} b^{n} c^{n} \mid n \geq 1\right\}$
Für jedes Wort aus dem Durchschnitt der beiden Sprachen kann man entweder über $S_1$ oder $S_2$ gehen.
Deshalb nicht eindeutig (für alle Wörter).
Bemerkung: Kontextfreie Sprachen sind nicht unter Durchschnitt abgeschlossen.

Normalformen für kontextfreie Grammatiken

Kontextfrei bedeutet dass die Ableitungs-Art keine Rolle spielt und man immer die selbe Sprache erzeugt.

Normalform bedeutet eine Einschränkung der rechten Seite der Produktionen $\beta$ .

Reduzierte Grammatik (Vorbereitung für Chomsky NF)

Reduzierte Grammatik

Wir möchten aus einer kontextfreien Sprache $L$ ohne $\varepsilon$ eine kontextfreie Grammatik erzeugen:

ohne nutzlose Produktionen
Produktionen die nicht vom Startsymbol erreichbar sind: $\small w \notin T^*$
Symbole $\in (N\cup T)$ die in keiner Satzform enthalten sind.

ohne $\small \varepsilon$ -Produktionen
$\small N\rarr \varepsilon$

ohne Einheits-Produktionen
$\small N\rarr N$

Ausgehend von einer existenten Grammatik $G$ .

Die erzeugte Sprache bleibt gleich.

$G=\langle N, T, P, S\rangle$ Ursprüngliche Grammatik

$G_{i}=\left\langle N_{i}, T_{i}, P_{i}, S\right\rangle, \quad1 \leq i \leq 4$ Erzeugten Grammatiken (anderer Index per Schritt)

Entfernen nutzloser Produktionen

Alle Nonterminale und Produktionen die zu einem Terminalwort führen:
$N_{1}^{(1)}=\left\{A \in N \mid A \rightarrow w \in P, w \in T^{*}\right\}$
$N_{1}^{(i)}=\left\{A \in N \mid A \rightarrow w \in P, w \in\left(N_{1}^{(i-1)} \cup T\right)^{*}\right\} ~~ \cup ~~N_{1}^{(i-1)}$
bis $N_{1}^{(m+1)}=N_{1}^{(m)}$ für ein beliebiges $m$ .
Dann erhalten wir
$\color{pink} G_{1}=\left\langle N_{1}, T, P_{1}, S\right\rangle$
$N_{1}=N_{1}^{(m)}$ — wobei $N_1 = \{A \in N\mid A \Rarr^* w \in T^*\}$
$P_1$ enhält nur alle Produktionen mit den gewählten Symbolen
Die Sprache ist leer $L(G)=\{\}$ wenn $S \notin N_{}^{(m)}$

Alle Symbole $V \sube(N \cup T)$ die vom Startsymbol erreichbar sind:
$V_{2}^{(1)}=\{S\}$
$u, v \in\left(N_{1} \cup T\right)^{*}$
$\begin{gathered}V_{2}^{(i)}=\{\alpha \in N_{1} \cup T \mid A \rightarrow u~\alpha~v \in P_{1},~~ A \in\left(V_{2}^{(i-1)} \cap N_{1}\right) \left.\right\}~~\cup ~~V_{2}^{(i-1)}\end{gathered}$
bis $V_{2}^{(m+1)}=V_{2}^{(m)}$
$\small A$ besteht nur aus den Nonterminalen aus dem letzten Schritt $\small (i-1)$ .
Dann erhalten wir
$\color{pink}G_{2}=\left\langle N_{2}, T_{2}, P_{2}, S\right\rangle$
$N_{2}=V_{2}^{(m)} \cap N_{1}$
$T_{2}=V_{2}^{(m)} \cap T_{1}$
$P_2$ enhält nur alle Produktionen mit den gewählten Symbolen $N_2 \cup T_2$

Enfernen von $\varepsilon$ -Produktionen

$N_3$ ist die Menge aller Nonterminale die zu einem $\varepsilon$ führen.

$N_{3}^{(1)}=\left\{A \in N_{2} \mid A \rightarrow \varepsilon \in P_{2}\right\}$

$N_{3}^{(i)}=\left\{A \in N_{2} \mid A \rightarrow w \in P_{2}, w \in\left(N_{3}^{(i-1)}\right)^{*}\right\} ~~\cup ~~N_{3}^{(i-1)}$

Aus $S \in N_{3}^{\left(|N_{2}|\right)}$ folgt, dass $\varepsilon \in \mathcal{L}\left(G_{2}\right)$

Dann erhalten wir $\color{pink}G_{3}$

Für $P_3$ nehmen wir anstatt von Produktionen aus $P_2$ :

$A \rightarrow X_{1} \ldots X_{k}$ mit $X_{i} \in N_{2} \cup T$

jetzt die Produktionen

$A \rightarrow Y_{1} \ldots Y_{k}$

für die gilt

$Y_{1} \ldots Y_{k} \neq \varepsilon$ // kein $\varepsilon$ auf rechter Seite

$Y_{i}=X_{i}$ wobei $X_{i} \in N_{2}-N_{3}^{\left({|N_2|}\right)}$

$Y_{i}=\varepsilon$ nur erlaubt falls $X_{i} \in N_{3}^{\left(|N_{2}|\right)}$ // sollte es $S \rarr \varepsilon$ geben dann belassen

Dadurch: $\mathcal{L}\left(G_{3}\right)=\mathcal{L}(G)-\varepsilon$

Entfernen von Einheits-Produktionen

Für alle $B_{0} \rightarrow B_{1} \in P_3:$

$B_{0} \Rightarrow B_{1} \Rightarrow B_{2} \Rightarrow \ldots \Rightarrow B_{k} \Rightarrow w,~~~w \notin N_{3}$

(Der letzte Schritt $k$ ist keine Einheitsproduktion)

Wir ersetzen $B_0 \rarr B_1$ mit $B_0 \rarr w$

Dadurch können wieder nutzlose Symbole entstehen.

Deshalb muss man hier wieder Schritt 1, 2 ausführen.

Dann erhalten wir $\color{pink}G_{4}$

Chomsky Normalform

Alle Produktionen besitzen die Form:

$N \rarr NN$

$N \rarr T$

Wenn $S \notin \beta:$ auch $S \rarr \varepsilon$ erlaubt damit Leerwort erzeugt werden kann.

Satz

Für jede kontexfreie Grammatik lässt sich eine äquivalente Chomsky-NF konstruieren.

Beweis

Wenn $\mathcal{L}(G)=\{\}$ - fertig.

Wenn $\mathcal{L}(G) \neq\{\}$

Aus $G$ die reduzierte Grammatik $G_{4}=\left\langle N_{4}, T_{4}, P_{4}, S\right\rangle$ erzeugen
Diese erzeugt: $\mathcal{L}(G)-\varepsilon$

Aus $G_4$ die Chomsky NF $G'$ erzeugen.
Für jede Produktion in $P_4$
- Falls rechte Seite nicht nur aus einem Terminal $a\in T$ besteht,
  jedes Terminal ersetzen mit $X_a$ .
  $X_a \rarr a$ hinzufügen
- Für $A, B \in N$ , jede Produktion $A \rightarrow B_{1} \ldots B_{k}$
  ersetzen mit $A \rightarrow B_{1} Y_{1},~~ Y_{1} \rightarrow B_{2} Y_{2},~~\ldots,~~ Y_{k-2} \rightarrow B_{k-1} B_{k}$

Falls $\varepsilon \in L(G)$
Wenn $S \notin \beta:$ auch $S \rarr \varepsilon$ hinzufügen.
Wenn $S \in \beta:$
neues $S''$ hinzufügen zu $N'$
Produktionen $\left\{S'' \rightarrow w \mid S \rightarrow w \in P'\right\}$ hinzufügen

Greibach Normalform

Wenn $S \notin \beta:$ auch $S \rarr \varepsilon$ erlaubt damit Leerwort erzeugt werden kann.

Greibach Normalform

Alle Produktionen haben die Form

$N \rarr TN^*$

Erweiterte Greibach Normalform

Alle Produktionen haben die Form

$N \rarr T(N\cup T)^*$

Satz

Für jede kontexfreien Grammatik lässt sich eine äquivalente (auch erweiterte) Greibach-NF konstruieren.

Übersicht: Alle eingeschränkte Varianten

Seien Produktionen der Form: $\alpha \rightarrow \beta \in P$

Überall wenn $S \notin \beta:$

auch $S \rarr \varepsilon$ erlaubt damit Leerwort erzeugt werden kann.

Kontextsensitive Grammatik

Für alle Produktionen gilt

$\alpha \in (N \cup T)^{*} \times N \times (N \cup T)^{*}$ (Nonterminal umgeben von Kontext)

$\beta \in (N \cup T)^{*} \times (N \cup T)^{+} \times (N \cup T)^{*}$

kontextsensitive Grammatik $\leftrightarrows$ monotone Grammatik

Kontextfreie Grammatik

Für alle Produktionen gilt

$\alpha \in N$

Reguläre Grammatik

Es gibt links- und rechts-regulären Sprachen.

Für alle Produktionen gilt

$N \rightarrow T \cdot N$

$N \rightarrow \varepsilon$

oder

$N \rightarrow T \cdot N$

$N \rightarrow T$

Reguäre Sprache $\leftrightarrows$ deterministischer endlicher Automat DEA $\leftrightarrows$ reguläre Grammatik

Umwandlung
$\mathcal{A}=\left\langle Q, \Sigma, \delta, q_{0}, F\right\rangle$
$G=\left\langle Q, \Sigma, P, q_{0}\right\rangle$
$q \rightarrow a p \in P$ wenn $\delta(q, a)=p$
$q \rightarrow \varepsilon \in P$ wenn $q \in F$
$\delta^{*}\left(q_{0}, w\right) \in F$ wenn $q_{0} \Rightarrow^{*} w$

Monotone Grammatik

$\alpha \neq \varepsilon$

Wenn für jede Produktion gilt: $|\alpha| \leq |\beta|$

kontextsensitive Grammatik $\leftrightarrows$ monotone Grammatik