Semantik formalisieren

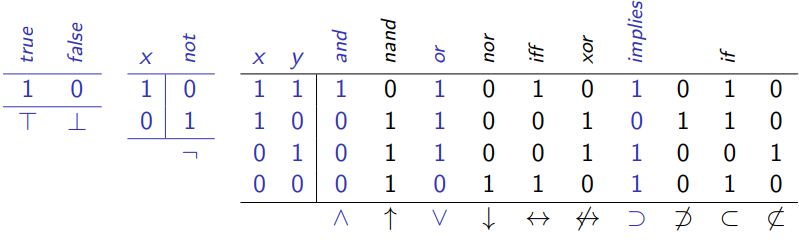
Semantik der Aussagenlogik

Auswertungsfunktion der Aussagenlogik

$\mathcal{B}=\{\mathbf{f}, \mathbf{t}\}$ Wahrheitswerte

$I: A V \mapsto \mathcal{B}$ Interpretation

$\mathcal{I}=\{I \mid I: A V \mapsto \mathcal{B}\}$ Environment

Auswertung von Aussagenlogische Formeln mit Interpretation festgelegt durch Funktion:

$\text {val : } \mathcal{I} \times \mathcal{A} \mathcal{F} \mapsto \mathcal{B}$

$\operatorname{val}_{I}(A)=I(A)$
wenn $A \in A V$

$\operatorname{val}_{I}(T)=\mathbf{t}$
wenn $\operatorname{val}_{I}(\perp)= \mathbf{f}$

$\operatorname{val}_{I}(\neg F)=\text { not } \operatorname{val}_{I}(F)$

$\operatorname{val}_{I}((F * G))=\operatorname{val}_{I}(F) \circledast \operatorname{val}_{I}(G)$
wobei $\circledast$ die logische Operation zu $*$ ist.

Aussagenlogische Funktionen

Wichtig: Wir nutzen hier $\equiv$ um metasprachliche Äquivalenz auszudrücken.

Semantik der Prädikatenlogik

Ausdrucksstärke der Prädikatenlogik

Beispiel: Relation
Prädikat: " $R$ ist eine Äquivalenzrelation" mit Signatur $\langle\{\underline{R}\},\{\},\{\}\rangle$ lässt sich ausdrücken als $F_{1} \wedge F_{2} \wedge F_{3}$ .
$\begin{aligned}&F_{1}=\forall x \underline{R}(x, x) \\&F_{2}=\forall x \forall y[\underline{R}(x, y) \supset \underline{R}(y, x)] \\&F_{3}=\forall x \forall y \forall z[(\underline{R}(x, y) \wedge \underline{R}(y, z)) \supset \underline{R}(x, z)]\end{aligned}$

Prädikatenlogische Interpretation $\small \mathcal I=\langle D, \Phi, \xi\rangle$

Zur Erinnerung:

Signatur $\small \Sigma$ als Menge von Symbolen

Modellstruktur $\small \mathcal D$ als Beziehungen zwischen Symbol und Funktion für meaning-function

Prädikatenlogische Interpretation über Signatur $\small \Sigma=\left\langle P S_{\Sigma}, K S_{\Sigma}, F S_{\Sigma}\right\rangle$ :

$\small D$ Domäne

$\small \Phi$ Signaturinterpretation

Man übergibt der Funktion $\small \Phi$ ein Symbol und erhält die jeweilige Funktion.

$\small P \in P S_{\Sigma} \longrightarrow \Phi(P): D^{n} \mapsto\{\mathbf{f}, \mathbf{t}\}$

$\small c \in K S_{\Sigma} \longrightarrow \Phi(c) \in D$

$\small f \in F S_{\Sigma} \longrightarrow \Phi(f): D^{n} \mapsto D$

$\small \xi$ Variablenbelegung

$\small \xi: I V S \mapsto D$

Man sagt man interpretiert einen Ausdruck über eine (Modell-)Struktur $\small \mathcal{D}$ (zB $\small \mathbb{Z}, \mathbb{N}, \mathbb{S}$ ) und Variablenbelegung $\small I$ .

Jede PL-Interpretation $\small \mathcal I$ bestimmt eine Modellstruktur $\small \mathcal{D}_{\mathcal{I}}=\left\langle D ; P_{D}, K_{D}, F_{D}\right\rangle$ und Variablenbelegung:

Man erhält die Menge aller Funktionen für die Modellstruktur aus der PL-Interpretation, indem man alle Zeichen aus der Signatur in die $\small \Phi$ -Funktion einsetzt.

$\small P_{D}=\left\{\Phi(P) \mid P \in P S_{\Sigma}\right\}$

$\small K_{D}=\left\{\Phi(c) \mid c \in K S_{\Sigma}\right\}$

$\small F_{D}=\left\{\Phi(f) \mid f \in F S_{\Sigma}\right\}$

Die Menge aller PL-Interpretationen $\small \mathcal I$ : $\small PINT_{\Sigma}$

Auswertungsfunktion für PL-Formeln

$\operatorname{val}_{\mathcal{I}}: P I N T_{\Sigma} \times \mathcal{P} \mathcal{F}_{\Sigma} \rightarrow\{\mathbf{f}, \mathbf{t}\}$

$\small \operatorname{val}_{\mathcal{I}}(\top)=\mathbf{t}, \operatorname{val}_{\mathcal{I}}(\perp)=\mathbf{f}$

$\small \operatorname{val}_{\mathcal{I}}\left(P\left(t_{1}, \ldots, t_{n}\right)\right)=\Phi(P)\left(\mathcal{M}_{\mathcal{T}}\left(\xi, t_{1}\right), \ldots, \mathcal{M}_{\mathcal{T}}\left(\xi, t_{n}\right)\right)$

$\small \operatorname{val}_{\mathcal{I}}(s=t)=\mathbf{t}$
genau dann wenn $\small \mathcal{M} \mathcal{\tau}(\xi, s)=\mathcal{M} \mathcal{T}(\xi, t)$ sonst $\small \mathbf f$ .

$\small \operatorname{val}_{\mathcal{I}}(\neg F)=\neg \operatorname{val}_{\mathcal{I}}(F)$

$\small \operatorname{val}_{\mathcal{I}}((F \wedge G))=\operatorname{val}_{\mathcal{I}}(F) \text { and } \operatorname{val}_{\mathcal{I}}(G)$

$\small \operatorname{val}_{\mathcal{I}}((F \vee G))=\operatorname{val}_{\mathcal{I}}(F) \text { or } \operatorname{val}_{\mathcal{I}}(G)$

$\small \operatorname{val}_{\mathcal{I}}((F \supset G))=\operatorname{val}_{\mathcal{I}}(F) \text { implies } \operatorname{val}_{\mathcal{I}}(G)$

$\small \operatorname{val}_{\mathcal{I}}(\forall v F)=\mathbf{t} \Longleftrightarrow \operatorname{val}_{\mathcal{I}^{\prime}}(F)=\mathbf{t} \text { für alle } \mathcal{I}^{\prime} \stackrel{v}{\sim} \mathcal{I}$

$\small \operatorname{val}_{\mathcal{I}}(\exists v F)=\mathbf{t} \Longleftrightarrow \operatorname{val}_{\mathcal{I}^{\prime}}(F)=\mathbf{t} \text { für ein } \mathcal{I}^{\prime} \stackrel{v}{\sim} \mathcal{I}$

$\small \mathcal{I}^{\prime} \stackrel{v}{\sim} \mathcal{I}$ bedeutet

$\small \mathcal{I}=\langle D, \Phi, \xi\rangle$

$\small \mathcal{I}^{\prime}=\left\langle D, \Phi, \xi^{\prime}\right\rangle$

Und das wiederum bedeutet $\small \xi \stackrel{v}{\sim} \xi^{\prime}$ :

Gleiche Variablenbelegung $\small \xi(w)=\xi^{\prime}(w)$ für alle Variablen $\small w \in IVS$ außer der Variable $v$ (also $\small v \ne w$ ). Denn $\small v$ ist die Variable die vom Quantor gebunden wurde.

Semantische Grundbegriffe

Formel $F \in \mathcal{P F}_{\Sigma}$

(allgemein) gültig wenn für alle $\mathcal{I} \in P I N T_{\Sigma}$ immer $\operatorname{val}_{\mathcal{I}}(F)=\mathbf{t}$

Immer wahr - dann nennt man es "Tautologie"

Alle Interpretationen sind Modelle

erfüllbar wenn für mindestens eine $\mathcal{I} \in P I N T_{\Sigma}$ gilt $\operatorname{val}_{\mathcal{I}}(F)=\mathbf{t}$

Mind. bei 1 Fall wahr - dann nennt man es "Modell vonF"

widerlegbar wenn für mindestens eine $\mathcal{I} \in P I N T_{\Sigma}$ gilt $\operatorname{val}_{\mathcal{I}}(F)=\mathbf{f}$

Mind. bei 1 Fall falsch - dann nennt man es "Gegenbeispiel" / "Gegenmodell"

unerfüllbar wenn für alle $\mathcal{I} \in P I N T_{\Sigma}$ immer $\operatorname{val}_{\mathcal{I}}(F)=\mathbf{f}$

Immer falsch

Alle Interpretationen sind Gegenbeispiele

Bei einer Menge von Formeln $F$ : $\mathcal{F} \subseteq \mathcal{P F}_{\Sigma}$

erfüllbar wenn für mindestens eine $\mathcal{I} \in P I N T_{\Sigma}$ gilt $\forall f\in F: \operatorname{val}_{\mathcal{I}}(f)=\mathbf{t}$

widerlegbar wenn für mindestens eine $\mathcal{I} \in P I N T_{\Sigma}$ gilt $\forall f\in F: \operatorname{val}_{\mathcal{I}}(f)=\mathbf{f}$

Für gegebene Modellstrukturen $\mathcal D$ und Signaturinterpretationen $\Phi$ - sind Formeln $F \in \mathcal{P F}_{\Sigma}$

zB erfüllbar in $\mathcal D$ bezüglich $\Phi$ wenn es mindestens ein $\mathcal{I}$ gibt mit $\mathcal{D_I=D}$ für das gilt $\operatorname{val}_{\mathcal{I}}(F)=\mathbf{t}$ .

Dann heißt $\mathcal I$ bezüglich $\Phi$ ein Modell von $\mathcal D$ in $F$ für alle $\xi$ .

Satz

$F$ hat keine endlichen Modelle.

Für alle Interpretationen $\mathcal I$ folgt mit $\operatorname{val}_{\mathcal{I}}(F)=\mathbf{t}$ , dass die Domäne $D$ unendlich ist.

Modellierung mit PL

Auswahl der Stelligkeit

Richtige Anzahl hängt vom Kontext ab

Beispiel
" Max liest Zeitung "
Mögliche Prädikate:
(0-stellig) $\text {Max\_liest\_Zeitung }$
(1-stellig) $\text{Liest\_Zeitung(max)}$ 
(2-stellig) $\text{Liest(max, zeitung)}$

Formalisierung natürlicher Sprache

Eigenschafen → Nomen
Immer die Nomen als Argument nutzen, nie Eigenschaften
Vermeiden: $\text{Sokrates\_ist(sterblich)}$ 
Sinnvol: $\text{Ist\_sterblich(sokrates)}$

Pronomen
"max liebt mia - mia liebt max"
Sinnvoll: $\text{Liebt(mia, max)} \wedge \text{Liebt(max, mia)}$

Unbestimmte Fürwörter
"Ich kann nichts sehen."
$\neg \exists x \text { Kann\_sehen}(\text {chris, } x)$

Fürwörter, Bindewörter
"Vor mir ist etwas großes und es ist hungrig."
$\exists x(\text {Befindet\_sich\_vor}(x, \text { chris}) \wedge \operatorname{Groß}(x) \wedge \text { Hungrig }(x))$

Quantoren, Typen und Beziehungen
"Jeder Student ist jünger als irgendein Professor."
$\forall x(\operatorname{Stud}(x) \supset \exists y(\operatorname{Prof}(y) \wedge \operatorname{Jünger}(x, y)))$
"Alle vernünftigen Leute verabscheuen Gewalt"
$\forall x(\text {Vernünftig}(x) \supset \text { Verabscheut}(x, \text { gewalt}))$
"Es gibt vernünftige Leute die Gewalt verabscheuen"
$\exists x(\text { Vernünftig }(x) \wedge \text { Verabscheut }(x, \text { gewalt }))$
Vertauschung von unterschiedlichen Quantoren
"Jeder hat eine Mutter"
$\forall x \exists y \text { Mutter}(y, x)$
$y$ hängt vom gewählten $x$ ab
"Jemand ist die Mutter von allen"
$\exists y \forall x \operatorname{Mutter}(y, x)$
$y$ ist unabhänging vom gewählten $x$

Funktionssymbole
"Jedes Kind ist jünger als seine Mutter"
$\forall x \forall y[(\operatorname{Kind}(x) \wedge \operatorname{Mutter}(y, x)) \supset \operatorname{Jünger}(x, y)]$
Dadurch wird nicht berücksichtigt, dass jedes Kind eine biologische Mutter hat.
Mutter sollte besser als Funktion aufgefasst werden, die jedem Kind seine eindeutig bestimmte Mutter zuordnet.
$\forall x(\text {Kind }(x) \supset \operatorname{Jünger}(x, \text { mutter }(x))$
Eindeutige Beziehung

Beschränkung der Anzahl
"Eva hat höchstens 2 Söhne"
$\exists x \exists y \forall z(\operatorname{Sohn}(z, \text { eva }) \supset(z=x \vee z=y))$
"Kain hat mindestens 3 Söhne"
$\exists x \exists y \exists z(\operatorname{Sohn}(x, \text { kain}) \wedge \operatorname{Sohn}(y, \text { kain}) \wedge \operatorname{Sohn}(z, \text { kain}) \\~~ \wedge ~x \neq y \wedge x \neq z \wedge y \neq z)$

Formalisierung formaler Inhalte

Nicht-totale Funktionen als nach-eindeutige Relationen

Relation $R\left(x_{1}, \ldots, x_{n}, x_{n+1}\right)$ ist nach-eindeutig in $\mathcal D$ wenn gilt:

$\forall \textcolor{pink}y \forall \textcolor{pink}z \forall x_{1} \cdots \forall x_{n}\left[\left(R\left(x_{1}, \ldots, x_{n}, \textcolor{pink}y\right) \wedge R\left(x_{1}, \ldots, x_{n}, \textcolor{pink}z\right)\right) \supset \textcolor{pink}y=\textcolor{pink}z\right]$

Satz von Gödel, Church, Turing

Jede partiell berechenbare Funktion lässt sich über $\N$ ausdrücken.

Logisches Schließen

Schlüsse, Konsequenz, Theorien

$\mathcal{F} \models_\mathcal{I} G$

$F_{1}, \ldots, F_{n} \models_{\mathcal{I}} G$

Immer wenn alle Prämissen / Annahmen in allen beliebigen Interpretationen $\mathcal I$ wahr sind, ist auch die Konklusion / Folgerung in $\mathcal I$ wahr.

Spezialfall: $\mathcal{F}=\{\}: ~~\models G$ bedeutet $G$ ist gültig.

$G$ folgt aus $\mathcal F$ genau dann wenn $\mathcal{F} \cup\{\neg G\}$ unerfüllbar ist.

Semantisches Schließen

$F_{1}, \ldots, F_{n} \models G$ genau dann wenn $F_{1} \supset\left(F_{2} \supset \cdots\left(F_{n} \supset G\right) \cdots\right)$ bzw $\left(F_{1} \wedge \cdots \wedge F_{n}\right) \supset G$ gültig ist.

Logische Äquivalenz

$F \lrarr G$ wenn $F \models G$ und $G \models F$

bzw $\models(F \supset G) \wedge(G \supset F)$ .

Axiomatische Theorien

Eine Theorie ist eine Menge von Formeln.

Eine axiomatische Theorie $\mathcal T$ ist gegeben durch

eine Menge Axiome $\mathcal A$

sodass $\mathcal{T}=\{F \mid \mathcal{A} \models F\}$

Man sagt: $\mathcal A$ axiomatisiert $\mathcal T$ .

Wir wollen dass $\mathcal A$ möglichst endlich oder zumindest entscheidbar ist.

Theorie einer (Modell-)Struktur

Für jede Struktur $\mathcal I$ ist $\operatorname{Th}(\mathcal{I})=\left\{F \mid \operatorname{val}_{\mathcal{I}}(F)=\mathbf{t}\right\}$ die Theorie.

Logische Unabhängigkeit (von anderen Formeln)

Eine Formel $G$ heißt unabhängig von der Formel-Menge $\mathcal F$ , wenn

$\mathcal{F} \models G$ und $\mathcal F \models \neg G$ nicht gelten.

Dafür muss man zwei Modelle $\mathcal I, \mathcal I'$ finden für die gilt $\operatorname{val}_{\mathcal{I}}(G)=\mathbf{f}$ und $\operatorname{val}_{\mathcal{I}^{\prime}}(G)=\mathbf{t}$ .