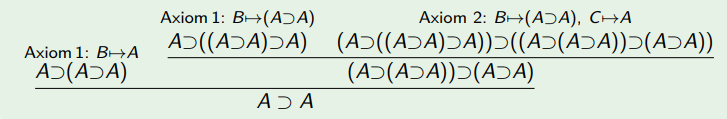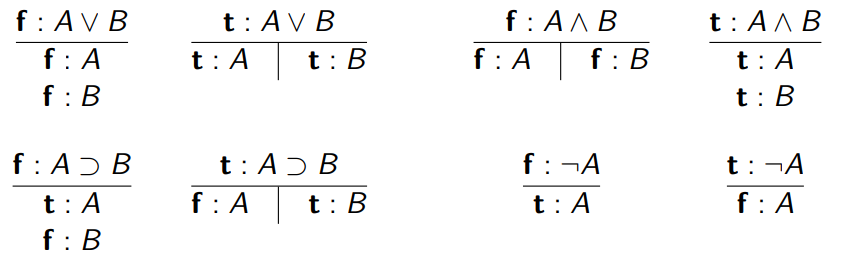Logischer KalkülK
formales Regelsystem, nimmt nur auf Syntax bezug
zeigt schrittweise die Gültigkeit von Formeln und Konsequenzbehauptungen
F1,…Fn⊢KG
Eigenschaften von Kalkülen
Korrektheit
(Syntax zu Semantik)
F1,…,Fn⊢KG⟹F1,…,Fn⊨G
Vollständigkeit
(Semantik zu Syntax)
F1,…,Fn⊢KG⟸F1,…,Fn⊨G
Hilbert-Typ-Kalkül
siehehttps://de.m.wikipedia.org/wiki/Hilbert-Kalkül
Beweissuche schwer zu automatisieren
Ableitungen entsprechen nicht natürlichsprachlichen mathematischen Argumentationsketten
Keine Beziehung zur Semantik
Vollständigkeit ist nicht einfach nachzuweisen (korrektheit schon)
Aussagenlogik
Logische Axiome
A,B
und
C
können gegen jede beliebige atomare Formel ausgetauscht werden
- (A⊃(B⊃A))
- ((A⊃(B⊃C))⊃((A⊃B)⊃(A⊃C)))
Nur eine Regel: Modus Ponens
BAA⊃B
Beispiel
Wir wollen
A⊃A
beweisen
Axiom 1:(A⊃(B⊃A))
Axiom 2:((A⊃(B⊃C))⊃((A⊃B)⊃(A⊃C)))
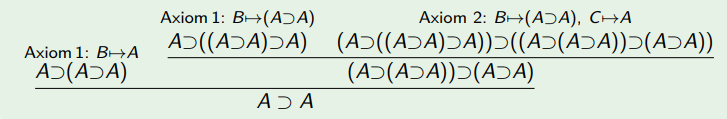 statt
B
in Axiom 1 setzen wir in der ersten Zeile
(A⊃A)
... usw.
statt
B
in Axiom 1 setzen wir in der ersten Zeile
(A⊃A)
... usw.


Prädikatenlogik
Frege-Hilbert-Typ-Kalkül für klassische PL
Gleichen Nachteile wie bei AL
Logische Axiome
A,B
und
C
können gegen jede beliebige atomare Formel ausgetauscht werden
- (A⊃(B⊃A))
- ((A⊃(B⊃C))⊃((A⊃B)⊃(A⊃C)))
…3. bis 9.
- A(x/t)⊃∃xA
t
muss in
A
frei für
x
sein
- ∀xA⊃A(x/t)
t
muss in
A
frei für
x
sein
Regeln
BAA⊃BB⊃∀xAB⊃A∃xA⊃BA⊃B
x
darf in
B
nicht frei vorkommen
(außer in der ersten Regel)
Tableau-Kalkül
Variante des Sequentialkalküls
Ein Tableau ist ein Baum von bewerteten Formeln als Tafel.
Sie können von Wahrheitstafeln abgelesen werden.
Grundidee: Beweis durch widerspruch
Wir gehen davon aus es gibt eine mögliche Interpretation für die Konsequenzbehauptung
F1,…,Fn⊨G
.
Beweis durch Widerspruch, durch Annahme dass
valI(F1)=t,…,valI(Fn)=t
valI(G)=f
für eine Interpretation
I
gilt (und folgert für Teilformeln.)
Beispiel
Tableau-Beweis von
(A⊃B)∧A⊨B
Wir wollen einen Widerspruch zeigen, deshalb:
1. Annahme:
t:(A⊃B)∧A
2. Annahme:
f:B
Wir zerlegen die Annahme
t:(A⊃B)∧A
t:A⊃B
t:A
Aus
t:A⊃B
folgt
f:A
t:B
Das steht im Widerspruch zu den vorherigen Annahmen.
Entscheidungsverfahren
Beweisversuch terminiert immer und vollständige Expansion liefert Beweis oder Gegenbeispiel.
Beweis = geschlossenes Tableau
Gegenbeispiel = offener Ast
Don't care Indeterminismus
Ergebnis ist unabhängig von Auswertungsreihenfolge.
Geschlossenheit von Ästen
(Hat nichts mit geschlossenen Formeln zu tun)
Wenn sowohl
t:F
als auch
f:F
vorkommen heißt der Tableau-Ast geschlossen, sonst offen.
Abschlussregel
Gelungenes Tableau-Beweis von einer Konsequenzbehauptung
F1,…,Fn⊨G
ist ein geschlossenes Tableau, mit Annahmen:
t:F1,…,t:Fn,f:G
.
Beweis vonFist ein geschlossenes Tableau mit Wurzelf:F
Vollständigkeit
Tableau-Beweis
⟹F1,…,Fn⊨G
Beweis
Lemma
Für
∨
Operator gilt:
val
I
(A∨B)=f⟺val
I
(A)=f und val
I
(B)=f
val
I
(A∨B)=t⟺val
I
(A)=t oder val
I
(B)=t
Analog für alle anderen Operatoren
Beweis der Vollständigkeit durch Widerspruch
Angenommen es stimmt nicht, dass "Tableau-Beweis⟹F1,…,Fn⊨G".
Also der Tableau-Beweis gelingt nicht aber die Konsequenzbehauptung stimmt.
Wenn ein vollständig expandiertes Tableau
offen
ist heißt das der Tableau-Beweis von
F1,…,Fn⊨G
gelingt nicht.
Das bedeutet es gibt kein GegenbeispielIfür die Konsequenzbehauptung.
Das bedeutet alle Äste sind offen.
Sei
Γ
ein
offener
,
vollständig expandierter
Ast.
Eine Aussagenvariable
A
kann für in diesem Ast nicht gleichzeitig wahr
t:A
und falsch
f:A
sein.
I(A)=t
falls
t:A
I(A)=f
falls
f:A
Durch das Lemma gilt das auch für Formeln.
(Induktion)
val
I
(F)=t
falls
t:F
val
I
(F)=f
falls
f:F
Und dadurch dass die wir eine eindeutige Interpretation haben, folgt daraus
val
I
(
F1
)
=t,…,val
I
(
Fn
)
=t
val
I
(G)=f
Das ist das Gegenbeispiel, von der wir behauptet haben, dass sie nicht existiert. ↯
Korrektheit
Tableau-Beweis
⟸F1,…,Fn⊨G
Beweis
Beweis der Korrektheit durch Widerspruch
Angenommen es stimmt nicht, dass "Tableau-Beweis⟸F1,…,Fn⊨G".
Also die Konsequenzbehauptung stimmt nicht aber der Tableau-Beweis gelingt.
Wenn ein vollständig expandiertes Tableau
geschlossen
ist heißt das der Tableau-Beweis von
F1,…,Fn⊨G
gelingt.
Wir nehmen an es gibt ein GegenbeispielIfürF1,…,Fn⊨Gwodurch wir wissen, dass sie nicht stimmen kann.
Es gilt
val
I
(
F1
)
=t,…,val
I
(
Fn
)
=t
val
I
(G)=f
.
Wegen dem Lemma gilt für jeden Ast
Γ
des Tableau:
val
I
(F)=t
falls
t:F
val
I
(F)=f
falls
f:F
Dadurch dass das Tableau geschlossen ist, muss auch jeder Ast geschlossen sein, wodurch gleichzeitig
t:F
und
f:F
auf dem Ast liegen müssen.
Wir müssten im Tableau auf ein Widerspruch stoßen, wodurch der Tableau-Beweis gelingen würde. ↯
Aussagenlogik
Tableau Expansion
(siehe unten)
Typen von Folgerungen:
α
-Regeln Konjunktion von kleineren Behauptungen
β
-Regeln Disjunktion von kleineren Behauptungen
Regeln
Eingeschränkte Syntax, mit nur
∨,∧,⊃,¬
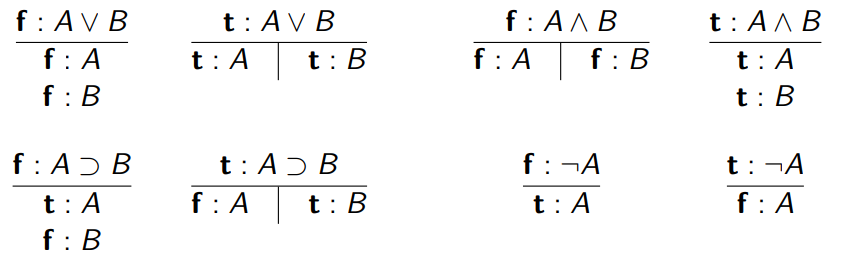 Für jede Operation
∘
gibt es 2 Regeln: für
f:A∘B
und für
w:A∘B
Für jede Operation
∘
gibt es 2 Regeln: für
f:A∘B
und für
w:A∘BPrädikatenlogik
💡
Wir beschränken uns auf geschlossene Formeln
F
.
Es kommen im PL-Tableau nie freie Variablen vor.
Begriffe
“Termtist frei fürxinF”
wenn
t
keine Variablen enthält die in
∀xF
oder
∃xF
gebunden sind.
“xist frei inF”
wenn
x
nicht an einem Quantor gebunden ist, also wenn
x∈FV(F)
.
“geschlossen”
F
ist geschlossen wenn
FV(F)={}
.
Term
t
ist geschlossen wenn es keine Variablen hat, also
FV(t)=V(t)={}
.
Regeln
Eingeschränkte Syntax, mit nur
∨,∧,⊃,¬
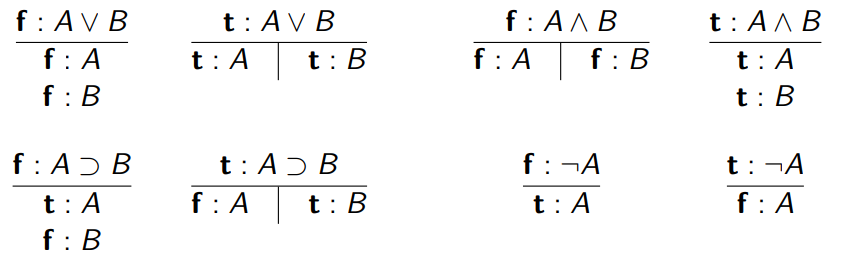 Für jede Operation
∘
gibt es 2 Regeln: für
f:A∘B
und für
w:A∘B
Für jede Operation
∘
gibt es 2 Regeln: für
f:A∘B
und für
w:A∘BTableau Expansion (mit Quantoren)
Σpar
Signatur erweitert mit den
Parameternc,d,e
α
-Regeln
w
1
:
F
1
w
:
F
w2:F2
β
-Regeln
w
1:
F
1∣
w
2:
F
2w:F
γ
-Regeln
t:F(x/t)t:∀xFf:F(x/t)f:∃xF
für beliebige geschlossene (ohne Variablen) TermetüberΣpa
r
.
(muss meistens öfter über die selbe Formel mit verschiedenentangewendet werden)
Erklärung
val
I
(∀x
F
)=t
für alle Interpretationen
I′∼xI
.
Daher auch in
val
I
(
F
(x/t))=t
für alle variablenfreien
t
.
(Eigentlich sogar auch für alletdie frei fürxinFsind → keine gebundenen Variablen ausFbeinhalten)
Analog fürval
I
(∃xF)=f
Problem
Wir können nicht garantieren, dass
alle
Elemente der Domäne durch einen Term repräsentiert werden.
δ
-Regeln
f:F(x/c)f:∀xFt:F(x/c)t:∃xF
für Parameterc∈Σpa
r
der bisher nicht vorgekommen ist
Erklärung
val
I
(∃x
F
)=
f
für mindestens eine der Interpretationen
I′∼xI
.
Analog fürval
I
(∀xF)=f
Problem
Wir wissen nicht welche Terme
t
wir für
x
substituieren dürfen und welche nicht.
Wir wissen nicht ob es einen variablenfreien Term gibt der einen "Zeugen" für
∃xF
repräsentiert.
Satz von Löwenheim-Skolen
Lösung für Probleme die mitγ-Regeln entstehen:
Σpar
Parameter: Erweiterung der Sprache um unendlich viele zusätzliche Konstanten
Lösung für Probleme die mitδ-Regeln entstehen:
Bei der Zerlegung von
f:∀xF
und
t:∃xF
muss der "Zeuge" für
Fneu
sein (also nicht im Tableau bisher vorgekommen sein).
Mit Gleichheits-Operator
💡
Wir beschränken uns auf geschlossene Formeln
FEs kommen im PL-Tableau nie freie Variablen vor
Atomare Formeln, können nur variablenfreie Terme enthalten.
Für die Terme
s,t
die in den folgenden Formeln vorkommen gilt
V(s)=V(t)={}
.
t:s=t
f:s=t
Abschlussregel für GleichheitsatomeAB=
(Abschlussregel für Tableaux siehe oben)
Wenn ein Ast die Formel
f:t=t
enthält, wird er geschlossen.
Substitutionssregel für GleichheitsatomeS=
t:s=tt:A[
s
/
t
]t:A[s]t:s=t
f
:A[
s
/
t
]
f
:A[s]t:s=tt:A[t]t:A[t/s]t:s=t
f
:A[
t
/
s
]
f
:A[t]
A[s]
Atom
A
enthält Term
s
(beliebig tief)
A[s/t]
Term
s
wird durch
t
ersetzt