Turingmaschinen

Turingmaschine ohne Arbeitsband

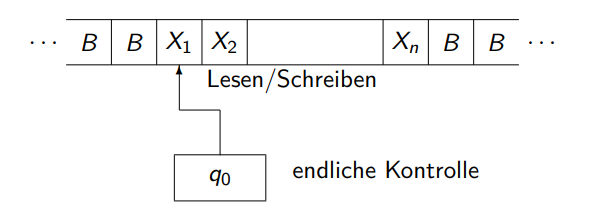
$\large M=\left(Q,~\Sigma,~\Gamma, ~\delta, ~q_{0}, ~B, ~F\right)$

Zustände $Q$

$q_0$ Anfangszustand

$F$ Endzustände

Eingabesymbole $\Sigma \sub \Gamma$

Symbole im Eingabewort (bevor es bearbeitet wurde).

Ansonsten ist das Verhalten undefiniert.

Bandsymbole $\Gamma$

Symbole im Eingabewort + die zum Überschreiben, zB. $B$

Übergangsfunktion $\delta$

Wenn deterministisch DTM:

$\delta: Q \times \Gamma \longmapsto Q \times \Gamma \times\{L, R, S\}$ (max. 1 Element aus der Zielmenge)

$\delta(q, X)=(p, Y, D)$

Wenn nicht deterministisch NTM:

$\delta(q, X)=\left\{\left(q_{1}, Y_{1}, D_{1}\right),\left(q_{2}, Y_{2}, D_{2}\right), \ldots,\left(q_{k}, Y_{k}, D_{k}\right)\right\}$

Was die Maschine tut:

Am Anfang ist der Kopf an der linkest möglichen Zelle.

Das Band ist links und rechts unendlich und mit Blanks gefüllt.

Basierend auf Zustand, Eingabe $\small X_i$ aus Band

Wechsel Zustand

Schreibe in Zelle

Bewege Kopf

Unterschiede zwischen Turingmaschinen

Alle Varianten von Turingmaschinen sind gleich mächtig.

Es gibt zu jeder NTM eine DTM.

DTM können dazu dienen Funktionen zu berechnen wenn man das Band als Input und als Output sieht.

NTM können dazu dienen Wörter zu erzeugen indem man mit einem leeren Band anfängt.

Akzeptanz von Sprachen

Konfiguration

$q X_{1} X_{2} \ldots X_{i-1} X_{i} X_{i+1} \ldots X_{n}$

Alternative Darstellung

$q$ aktuelle Position vom Kopf (ließt Element rechts davon)

$X$ Bandsymbole / Abschnitt des Bandes wo nicht unendlich viele Blanks sind.

Akzeptierte Sprache $L(M)$

Deterministische Turingmaschine

Sprache $L$ wird von $M$ akzeptiert, wenn ein Endzustand erreicht wird:

$L(M)=\left\{w \in \Sigma^{*} \mid q_{0} w \Rightarrow^{*} \alpha p \beta, \quad p \in F, \quad \alpha, \beta \in \Gamma^{*}\right\}$

Nicht-Deterministische Turingmaschine

Sprache $L$ wird von $M$ akzeptiert, wenn es möglich ist einen Endzustand zu erreichen.

Die Turingmaschine hält immer an, wenn sie einen Endzustand erreicht:

Endzustand mit $w$ erreichen bzw Wort akzeptieren $\Rarr$ Anhalten

$\small w \in L(M) \Rarr$ Anhalten

Das Anhalten bei einem Endzustand ist die Abbildung:

$\small \delta(q \textcolor{pink}{\in F}, X) = \text{undefined}$

Turingmaschine mit Arbeitsband

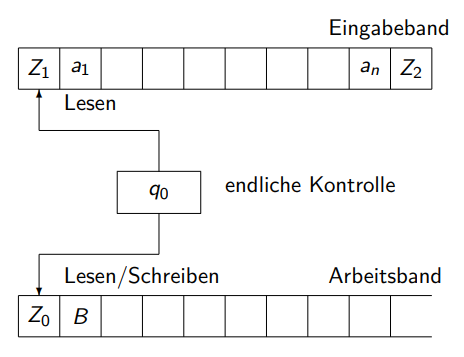
$\large M=\left(Q, T, \Gamma, \delta, q_{0},\left\{Z_{0}, Z_{1}, Z_{2}\right\}, B, F\right)$

Zustände $Q$

$q_0$ Anfangszustand

$F$ Endzustände

Eingabeband Symbole $T$ (nur lesen)

Symbole im Eingabewort sein können

Arbeitsband Symbole $\Gamma$ (lesen, schreiben)

Symbole im Eingabewort + die zum Schreiben wie $B$

Übergangsfunktion $\delta$

Wenn deterministisch DTM: (max. 1 Element aus der Zielmenge)

$\delta: Q \times T \times \Gamma\longmapsto Q \times \Gamma \times \{L, R, S\}\times\{L, R, S\}$

$\delta(q, a, X)=\left(p, Y, D_{E}, D_{A}\right)$

Zustand $\small q \mapsto p$

Eingabeband $\small a$

Arbeitsband $\small X \mapsto Y$

Position auf Eingabeband $\small D_E$

Position auf Arbeitsband $\small D_A$

Wenn nicht deterministisch NTM:

$\delta(q, a, X)=\{\left(q_1, Y_1, D_{E1}, D_{A1}\right), \left(q_2, Y_2, D_{E2}, D_{A2}\right),\dots \left(q_k, Y_k, D_{Ek}, D_{Ak}\right)\}$

Bregenzungssymbole

$Z_0$ Begrenzung Arbeitsband links

$Z_1,~Z_2$ Begrenzung Eingabeband

Eingeschränkte Varianten

Normalform von DTM

Nur 1 Endzustand

Arbeitsband nach Ausführung und Akzeptanz leer

Letzter Übergang:

$\small \delta(x, Z_{2}, Z_{0})=\left(f, Z_{0}, S, R\right)$ wobei $\small x$ beliebiger Zustand

Linear beschränkter Automat LBA

= EA + beschränkter RAM (Arbeitsband)

Arbeitsband darf max. linear so viel Platz beanspruchen wie Eingabewort.

$\small |\text{A}| = c\cdot |\text{E}| + d$

Kellerautomat KA (Pushdown automaton)

= EA + Stack

Nie nach links in Eingabeband: $\small D_E = \{R, S\}$

Leseschreibkopf darf links davon nur Nicht-Blank-Symbole haben, rechts davon nur Blank-Symbole.

Akzeptierte Sprache

Zwei Möglichkeiten zu definieren

In Endzustand

Stack ist leer

Endlicher Automat EA

Nützt Arbeitsband nicht

$\delta: Q \times T \longmapsto Q \times \{L, R, S\}$

$\delta(q, a)=\left(p, D_{E}\right)$

Alternativerweise - auch zugleich Kellerautomat (mit unbenutztem Stack)

$\delta: Q \times T \cup \{\varepsilon\} \longmapsto Q$

$\delta(q, a)=p$

$\delta(q, a\in T)=p$ zu interpretieren als $\small \delta(q, a, R)$

$\delta(q, a \in \varepsilon)=p$ zu interpretieren als $\small \delta(q, a, S)$