Human Irrationality

Evidence shows that humans are predictably irrational.

Normative theory How a rational agent should act = decision theory

Descriptive theory How actual agents really do act. (ie. humans)

Certainty Effect

Ambiguity aversion

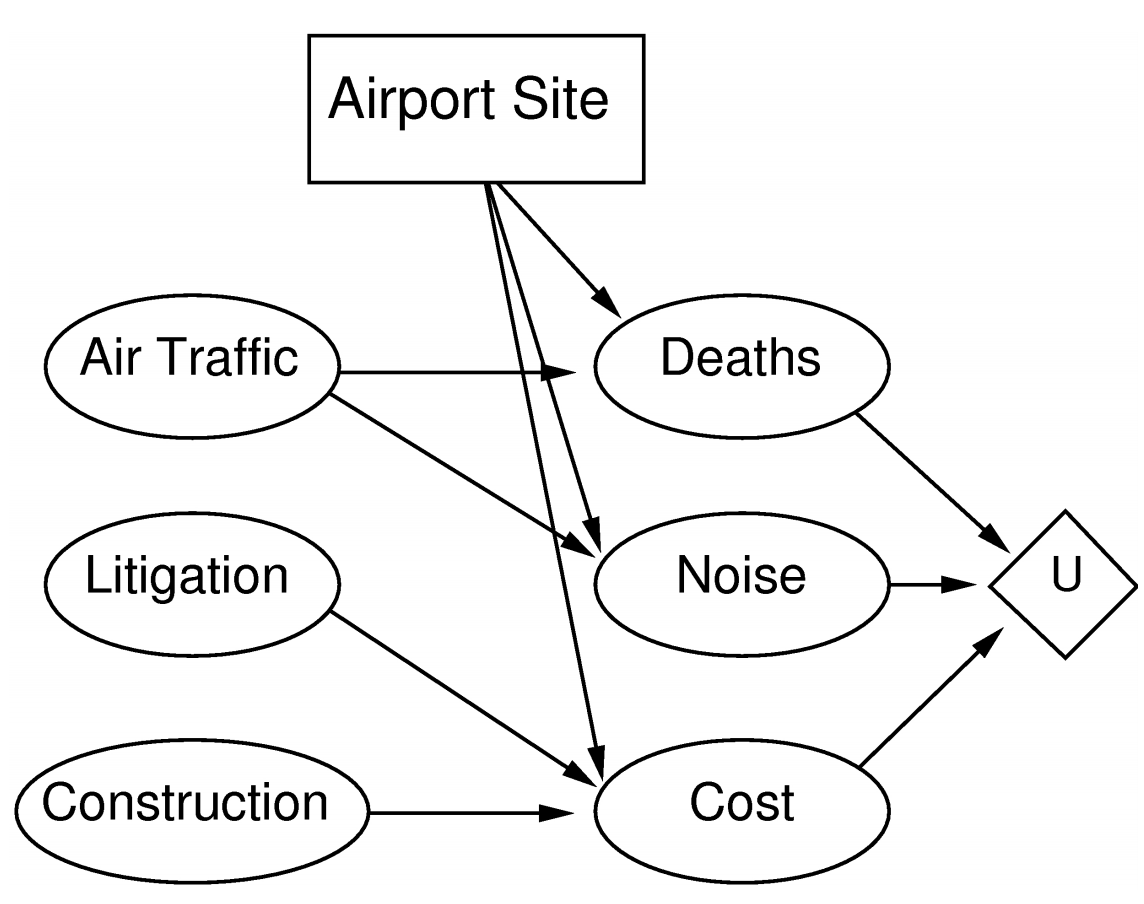
Decision Networks

= influence diagrams.

General framework for rational decisions - return the action with highest utility.

Decision networks are an extension of Bayesian networks.

Presents:

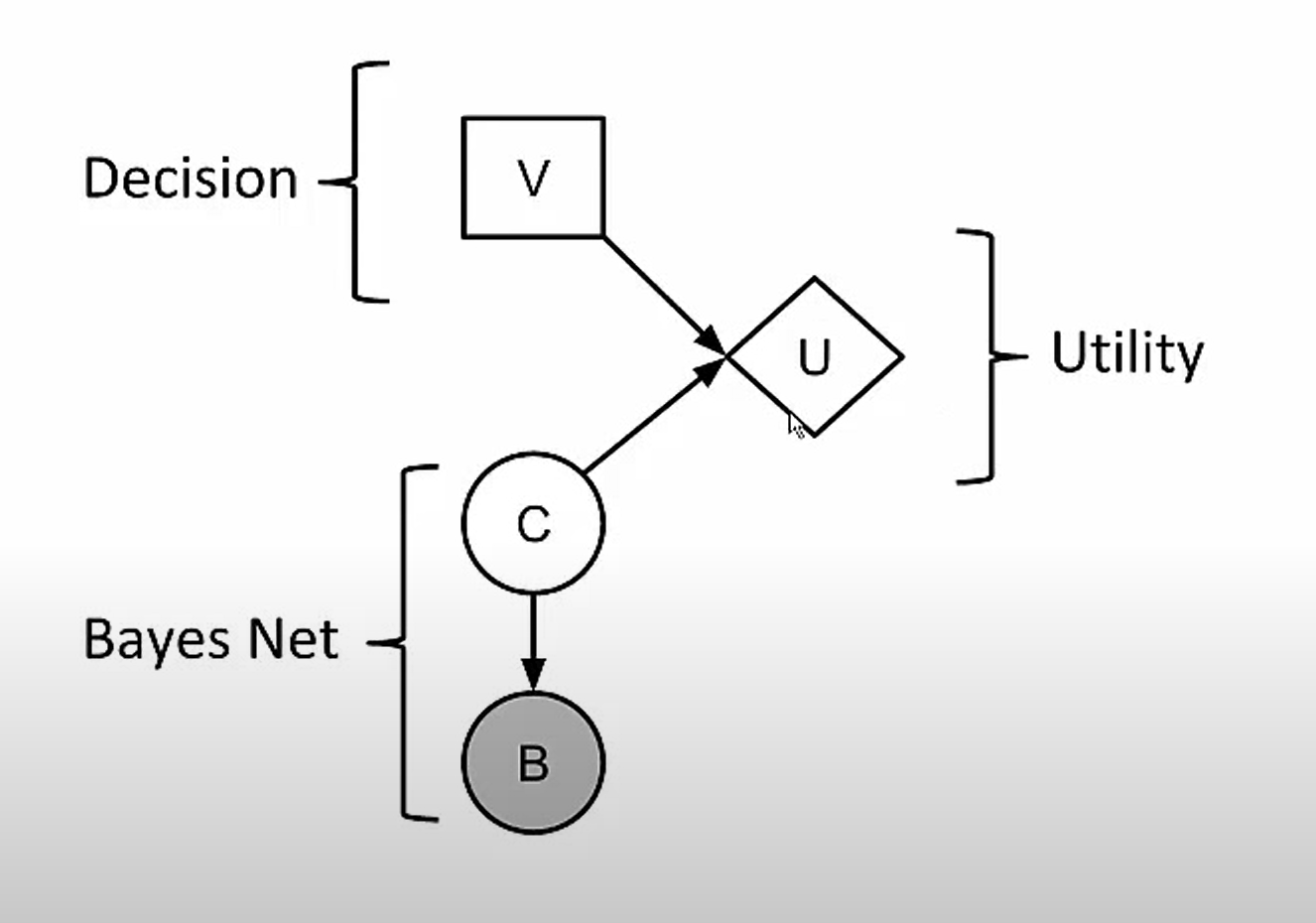
Node types:

Evaluating decision networks

Actions are selected by evaluating the decision network for each possible setting of the decision node. → Action with highest utility gets chosen.

Decision network algorithm

set evidence variables for current state
for each possible value of the decision node
1. set the decision node to that value
2. calculate the posterior probabilities for the parent nodes of the utility node,
using a standard probabilistic inference algorithm (with bayesian network)
2. calculate the resulting utility for the action
return the action with the highest utility

• Example: Airport siting problem

  Notice that, because the Noise, Deaths, and Cost chance nodes in refer to future states, they can never have their values set as evidence variables.

  

Information Value Theory

Data must be first extracted before analysis. We want to choose what information to acquire.

• Example: Doctor

  Doctor is not immediately provided with all possible diagnostic tests and questions.

  Tests are expensive and sometimes hazardous (directly and because of associated delays until treatment).

  Their importance depends on two factors:

  • whether the test results would lead to a significantly better treatment plan

  • how likely the various test results are.

Value of Information

$\text{value = }(\text{ avg. best action before obtaining}) - (\text{avg. best action after obtaining})$

• Example: Oil Company

  There are $n$ different indistinguishable blocks.

  $\frac{1}{n}$ blocks has oil worth $C$ dollars.

  Others are worthless.

  Blocks cost $\frac{C}{n}$ dollars.

  How much is the information whether a block 3 has oil or not worth to the company?

  • $P(\text{block has oil}) = \frac{1}{n}$

    If the block has oil, the company will buy it $-\frac{C}{n}$ and then profit $C$ dollars:

    $C − \frac{C}{n} = \frac{(n-1) \cdot C}{n}$

  • $P(\text{block has no oil}) = \frac{1}{n}$

    If the block has no oil, the company will buy a different block because the probability of finding oil in other ones changes from $\frac{1}{n}$ to $\frac{1}{n-1}$ .

    Average profit: of $\frac{C}{n-1} - \frac{C}{n} = \frac{C}{n(n-1)}$ dollars.

  We then calculate the expected / average profit with the information:

  $\frac{1}{n} \cdot \frac{(n-1) \cdot C}{n} + \frac{1}{n-1} \cdot \frac{C}{n(n-1)}= \frac{C}{n}$

  Which is equal to the price we would be for a block if we would not have had this information.

• Example: Oil Company (simplified)

  There are $n$ boxes.

  Opening a box costs costs $\frac{C}{n}$ dollars.

  $\frac{1}{n}$ boxes contains $C$ dollars, others are worthless.

  How much is the information whether box 3 has oil or not worth to the company?

  • $P(\text{box has prize}) = \frac{1}{n}$

    Then we will pay the price to open it and take the money inside: $C − \frac{C}{n}$

  • $P(\text{box has no prize}) = \frac{1}{n}$

    Then we will open another box - the probability of finding the prize changes from $\frac{1}{n}$ to $\frac{1}{n-1}$ and on average we make $\frac{C}{n-1} - \frac{C}{n}$ dollars.

  We then calculate the average profit with the information:

  $P(\text{box has prize}) \cdot (C − \frac{C}{n} ) + P(\text{box has prize}) \cdot (\frac{C}{n-1} - \frac{C}{n}) = \frac{C}{n}$

  Therefore this information has a value of $\frac{C}{n}$ .

  This is what it would cost us to find it out ourselves and we are willing to pay someone $<\frac{C}{n}$ to figure it out for us.

Value of perfect information VPI(= expected value of information)

Lets say the exact evidence $e_j$ (= perfect information) of the random variable $E_j$ is currently unknown.

We define:

Value of learning the exact evidence is the cost of discovering it for ourselves under $\mathbf{e}$ by averaging over all possible values $e_{jk}$ of $E_j$ .

VPI is non-negative

In the worst case, one can just ignore the received information.

$\forall \mathbf{e}, E_{j} \quad V P I_{\mathbf{e}}\left(E_{j}\right) \geq 0$

VPI is non-additive

The VPI can get higher or lower as new information gets aquired as combined information can have different effects.

$\operatorname{VPI}_{\mathbf{e}}\left(E_{j}, E_{k}\right) \neq V P I_{\mathbf{e}}\left(E_{j}\right)+\operatorname{VPI}_{\mathbf{e}}\left(E_{k}\right)$

VPI is order independent

$V P I_{\mathbf{e}}\left(E_{j}, E_{k}\right)=V P I_{\mathbf{e}}\left(E_{j}\right)+V P I_{\mathbf{e}, e_{j}}\left(E_{k}\right)=V P I_{\mathbf{e}}\left(E_{k}\right)+V P I_{\mathbf{e}, e_{k}}\left(E_{j}\right)$

Decision-theoretic Expert Systems

Decision analysis

Decision theory applied to actual decision problems.

The decision maker states preferences that the decision analyst then uses to find the optimal action / controlling if automated system behaves correctly.

Expert systems

Early expert system research concentrated on answering questions rather than on making decisions.

Decision networks allows to recommend optimal decisions, reflecting preferences as well as available evidence.

• are able to make decisions and use the value of information to decide whether to acquire it

• can calculate their sensitivity to small changes in probability and utility assessments.

The process of creating a decision-theoretic expert system

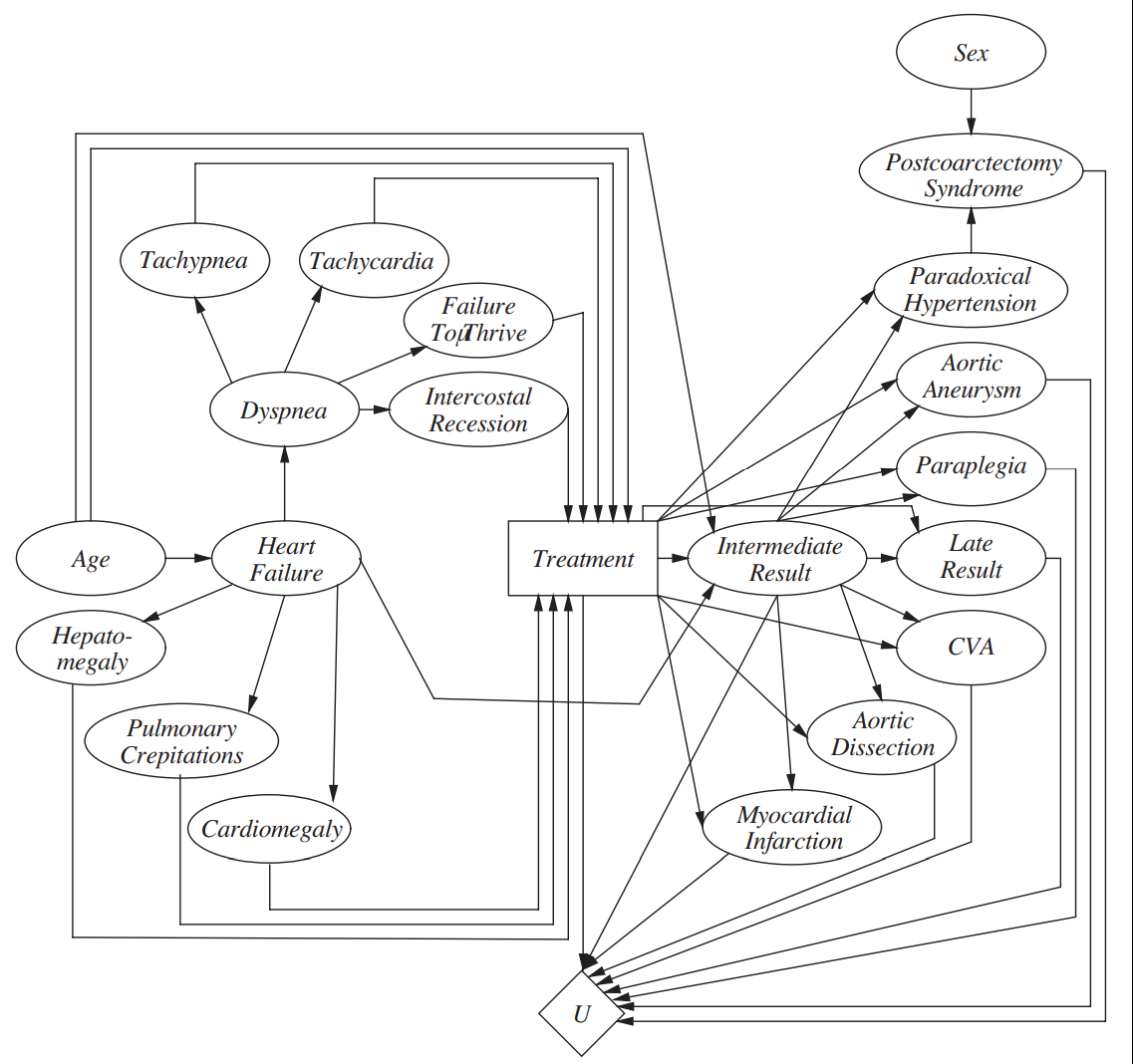
e.g., for selecting a medical treatment for congenital heart disease (aortic coarctation) in children

1. create a causal model

   (e.g., determine symptoms, treatments, disorders, outcomes, etc.)

2. simplify to a qualitative decision model

3. assign probabilities

   (e.g., from patient databases, literature studies, experts subjective assessments, etc.)

4. assign utilities

   (e.g., create a scale from best to worst outcome and give each a numeric value)

5. verify and refine the model, evaluate the system against correct input-output-pairs, a so called gold standard

6. perform sensitivity analysis

   (i.e., check whether the best decision is sensitive to small changes in the assigned probabilities and utilities.)