Utility Theory

Utility theory and probability theory (for decision-theoretic agents)

Decision theory

Non-deterministic, in partially observable environments

Outcome defined by random variable $\text{RESULT}(a)$ .

Probability of outcome $s'$ with given observations $\vec e$ .

Utility function

$U(s)$ desireability of state

Expected Utility (average utility value)

Its impicit that $s'$ can follow from the current state $s$ .

$E U(a \mid \mathbf{e})=\sum_{s^{\prime}} P(\operatorname{RESULT}(a)=s^{\prime} \mid a, \mathbf{e}) \cdot U(s^{\prime})$

Sum of: Probability of state occuring after action times its utility

Principle of maximum expected utility MEU

rational agent should choose the action that maximizes the agents expected utility

$\text { action }=\underset{a}{\operatorname{argmax}} \space E U(a \mid \mathbf{e})$

Axioms of Utility theory

Constraints on rational preferences of an agent - MEU can be derived from these constraints.

Notation:

Lottery

Set of possible outcomes for each action.

Constraints

1. Orderability

   The agent must have a preference.

   $(A \succ B) \space \textsf{xor} \space (B \succ B) \space \textsf{xor} \space (A \succsim B)$

2. Transivity

   $(A \succ B) \wedge(B \succ C) \Rightarrow(A \succ C)$

3. Continuity

   If $A \succ B \succ C$ there is a probability $p$ for which the agent would be indifferent to

   getting $B$ with absolute certainty

   or $A$ with probability $p$ and $C$ with $1-p$

   $A \succ B \succ C \Rightarrow \exists p\space[p, A ; 1-p, C] \sim B$

4. Substitutability

   If agent is indifferent to $A$ and $B$ then agent is indifferent to complex lotteries with same probabilities.

   $A \sim B \Rightarrow[p, A ; 1-p, C] \sim[p, B ; 1-p, C]$

5. Monotonicity

   Agent prefers a higher probability of the state that it prefers.

   $A \succ B \Rightarrow(p>q \Leftrightarrow[p, A ; 1-p, B] \succ[q, A ; 1-q, B])$

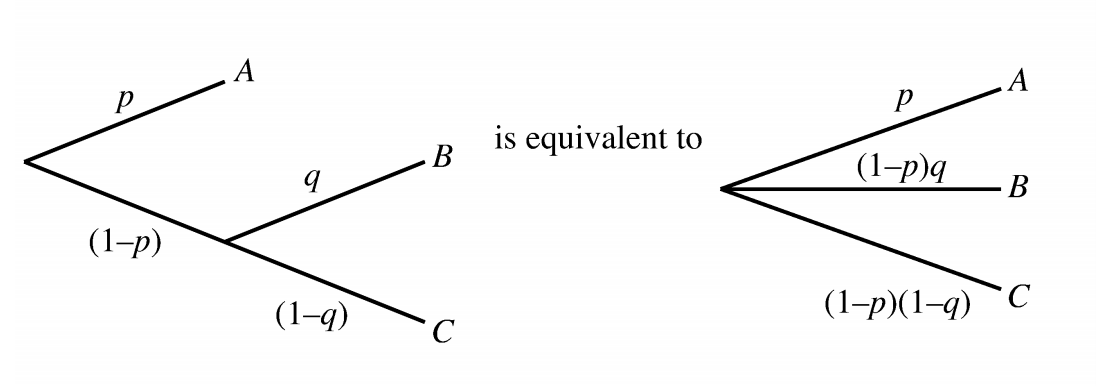
6. Decomposability

   Compound lotteries can be reduced to simpler ones.

   $[p, A ; 1-p,[q, B ; 1-q, C]] \sim[p, A ;(1-p) q, B ;(1-p)(1-q), C]$

If an agent violates these axioms it will exhibit irrational behaviour.

• Example: intransitive preferences

  $A \succ B \succ C \succ A$

  Agent can be induced to give away all its money:

  Agent has $A$

  1. We offer $A$ + 1 cent for $C$ (agent accepts)

  2. We offer $B$ + 1 cent for $C$ (agent accepts)

  3. We offer $A$ + 1 cent for $B$ (agent accepts)

  We repeat all over again.

  

Preference constraints → Utility Function

Existence of utility function

If agent is rational, there exists a real-valued function $U$ so that

The agents behavior would not change if:

It is therefore not something unique .

The numbers do not matter - this is a value / ordinal utility function .

Expected utility of a lottery

is the sum of the probability of each outcome times its utility.

Utility assessment and Utility scales

We want to build a decision theoretic system that helps the agent make decisions.

• Examples for utility scales

  micromort - one-in-a-million chance of death

  value that people place on their own lifes.

  ie. 1 micromort is equivalent to 20 USD (1980s money).

  QALY - quality-adjusted life year

  one QALY equates to one year in perfect health.

  is an indicator for the time-trade-off (TTO): to choose between being ill vs. being healthy but having a shorter life expectancy.

  ie. on average, kidney patients are indifferent between living two years on a dialysis machine and one year at full health

Preference elicitation

Testing / observing agent and finding out its underlying utility function.

There are no absolute values for utility function - we try to create it:

Normalized utilities

Utility of Money

Utility measure = agents total net assets.

Agents have monotonic preference for more money - they prefer having more.

That says nothing about preferences between lotteries involving money.

Expected monetary value EMV

The EMV (money made on average) ≠ the utility of it, because of:

• the agents current net asset

• risk-averseness of agent

Certainty equivalent

• reminder

  $U(L) < U(\textcolor{pink}{S_{EMV(L)}})$

  the utility of being faced with that lottery $<$ than the utility of being handed the expected monetary value of the lottery with absolute certainty

Most people will accept about $400 in alternative to playing a gamble that gives $1000 half the time and $0 the other half.

In this case:

Insurance premium

= EMV - certainty equivalent of a lottery

is based on risk aversion.

Risk neutral

For small changes in wealth relative to the current wealth, almost any curve will be approximately linear.

An agent that has a linear curve is said to be risk-neutral. This justifies the axioms of probability.