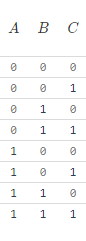
AB 1
Link zur Web Version dieser Notion page: https://www.notion.so/AB-1-816446f762064cb382bc9c13113cb248
✅ Aufgabe 1
Verlangt:
-
Zugrundeliegende Inferenzregel angeben → Gültigkeit bestimmen
-
"Falls in der Wahrheitsbelegung
alle
Prämissen
wahr sind, dann ist auch die
Konklusion
wahr in
."
(Kriterium für die Gültigkeit von Inferenzregeln)
(Wahrheitsbelegung = Interpretation)
- gültig wenn für alle Wahrheitsb. immer
- erfüllbar wenn für mindestens eine Wahrheitsb.
- widerlegbar wenn für mindestens eine Wahrheitsb.
- unerfüllbar wenn für alle Wahrheitsb. immer
-
"Falls in der Wahrheitsbelegung
alle
Prämissen
wahr sind, dann ist auch die
Konklusion
wahr in
."
(Kriterium für die Gültigkeit von Inferenzregeln)
- Weiteres Beispiel / Gegenbeispiel
a)
Es gibt Menschen die kriminell sind (wahr)
Alle Asylanten sind Menschen (wahr)
------------------------------------------
Alle Asylanten sind kriminell (falschFormel der Inferenzregel: ungültig (Generalisierung)
Alle x sind y Prämisse
z ist ein y Prämisse
------------------------------------------
z ist ein x KonklusionWeiteres Gegenbeispiel:
Alle Bälle sind rund (wahr)
Die Sonne ist rund (wahr)
-----------------------------------------
Die Sonne ist ein Ball (falsch) b)
Wenn alle Tober xetig sind
und ein Hituch ein Tober ist
------------------------------------------
Dann ist Hituch xetigInferenzregel: (gültig)
Alle t sind x
h ist ein t
------------------------------------------
h ist ein x Weiteres Beispiel aus dem Alltag:
Wenn alle Urgroßmütter Großmütter sind
und eine Großmutter eine Mutter ist
------------------------------------------
Dann ist eine Urgroßmutter eine Mutterc)
Alle Katzen miauen
Bello ist keine Katze
------------------------------------------
Also miaut Bello nichtInferenzregel: (ungültig)
Alle k sind m
b ist kein k
------------------------------------------
b ist kein mGegen-Beispiel aus dem Alltag:
Alle Männer sind Menschen
Frauen sind keine Männer
------------------------------------------
Frauen sind keine Menschen✅ Aufgabe 2
Jeden Satz einzeln Modellieren:
Wichtig: Elementaraussagen zeichnen sich dadurch aus, dass sie entweder richtig oder falsch sein können.
Liebe Kundin, lieber Kunde! Wir gratulieren zum Erwerb dieses Produkts! Legen Sie Hammer und Schraubenzieher oder Akkuschrauber bereit. Packen Sie die Plastikteile aus, aber beschädigen Sie dabei die Beschichtung nicht. Nur wenn Sie die Version 2.0 des Modells erworben haben, stecken Sie nun alle Teile zusammen. Falls nicht, müssen Sie alle Teile verleimen. Falls Sie beim Aufbau Probleme haben oder Teile fehlen, wenden Sie sich bitte an unsere Service-Hotline. Gutes Gelingen!
Legen Sie Hammer und Schraubenzieher oder Akkuschrauber bereit. Packen Sie die Plastikteile aus, aber beschädigen Sie dabei die Beschichtung nicht.
Kunde legt Werkzeuge (= Hammer / Schraubenzieher) bereit
Kunde packt Plastikteile aus
Kunde beschädigt die Beschichtung
Formel:
Nur wenn Sie die Version 2.0 des Modells erworben haben, stecken Sie nun alle Teile zusammen. Falls nicht, müssen Sie alle Teile verleimen.
Die vom Kunden erhaltene Version des Modells entspricht 2.0
Kunde steckt alle Teile zusammen
Kunde verleimt alle Teile
Struktur: Wenn dann , ansonsten wobei und gleichzeitig zutreffen dürfen aber wenn dann immer auch aber umgekehrt nicht zwingend.
Formel:
Unter der Annahme, dass:
- (Modell) bestimmt ob (zusammenstecken) oder (leimen) gewählt wird
- (leimen) führt immer zum (zusammenstecken) aber umgekehrt ist es optional.
Falls Sie beim Aufbau Probleme haben oder Teile fehlen, wenden Sie sich bitte an unsere Service-Hotline.
Kunde hat beim Aufbau Probleme
Es Fehlen Teile vom Produkt
Kunde nimmt mit Hotline Kontakt auf
Struktur: Falls oder dann aber sonst auch möglich.
Formel:
Unter der Annahme, dass:
- Man sich dem Service auch zuwenden kann, falls nicht die erwähnten Probleme bestehen
✅ Aufgabe 3
Maria kommt mit ins Kino
Clara kommt mit ins Kino
Peter kommt mit ins Kino
a)
Maria kommt mit ins Kino.
b)
Peter kommt vielleicht mit.
Das Wort vielleicht lässt sich nicht modellieren.
c)
Clara kommt mit, Peter aber nicht.
d)
Wenn Maria mitkommt, dann kommt Peter nicht mit.
e)
Nur wenn Maria mitkommt und Peter nicht, dann kommt Clara.
Annahme: Ansonsten kommt sie nicht.
Würde sie sonst auch kommen, dann:
f)
Wenn Peter nicht kommt, dann kommt Clara nicht, und wenn Clara nicht kommt, dann kommt Peter nicht.
g)
Mindestens eine(r) der drei kommt mit.
h)
Genau zwei kommen mit.
i)
Höchstens zwei kommen mit.
✅ Aufgabe 4
a)
Zeigen Sie, dass die Menge{iff, xor}vollständig ist für die Klasse der aussagenlogischen Funktionen.
Eine Menge von Funktionen heißt vollständig (für eine Funktionsklasse), wenn damit alle Funktionen (der Klasse) ausgedrückt werden können.
Beispiele
{not, and}, {nand}, {nor}, {not, or}, {not, implies}, {implies, false}
Man kann keine anderen Funktionen erzeugen, diese Menge ist nicht funktional vollständig .
Beweis: iff ist dual zu xor und man kann mit der Menge {xor} alleine beispielsweise nicht die Funktionen and sowie or bilden.
b)
Zeigen Sie, dass die Menge {iff, or} nicht vollständig ist.
Es reicht anzugeben dass eine einzige Funktion nicht darstellbar ist. - Ich nehme mir vor zu beweisen, dass die not Funktion nicht darstellbar ist, weil sie nur ein Argument beansprucht und ich intuitiv weiß, dass sie nicht mit iff oder or darstellbar ist.
Wir nutzen nur das Argument x (weil die not Funktion nur mit einem einzigen Argument arbeitet).
Hypothese
Jeder Ausdruck bestehend aus (n oder weniger) iff, or und x ist äquivalent zu x oder true .
Induktiver Beweis (wobei n = # der Anwendungen eines Operators)
Induktionsanfang: n := 0
Keine Operatoren - bedeutet x selbst.
Induktionsanfang: n := 1
Wenn wir eine beliebige Kombination der uns verfügbaren Funktionen nehmen:
-
-
Dann dürfen nur Kombinationen aus den Argumenten der Menge {iff, or} verwendet werden.
-
- → dadurch haben wir eine weitere Funktion in unserer Menge
Induktionsanfang: n := 2
Wenn wir eine beliebige Kombination der uns verfügbaren Funktionen nehmen:
-
-
Dann dürfen nur Kombinationen aus den Argumenten der Menge {iff, or} verwendet werden.
-
-
Induktionsschritt: n := n+1
Für jeden weiteren rekursiven Einsatz kann nur (effektiv) mit den bereits ausgewerteten Ausdrücken von den vorherigen Schritten gearbeitet werden.
Dadurch können wir aber nicht die Funktion ausdrücken - wodurch die Bedingung für funktionale Vollständigkeit verletzt ist.
Alternativerweise:
Dadurch, dass iff die duale funktion zu xor ist:
lässt sich dieses Problem reduzieren auf das Problem "Zeigen Sie, dass die Menge {or, xor} nicht vollständig ist."
Siehe: Lösungen vom vergangenen Jahr.
✅ Aufgabe 5
Sei die Formel
a)
Syntaktische Korrektheit
Die Menge der aussagenlogischen Formeln ist die kleinste für die gilt:
- (eine Variable ist eine gültige Formel)
-
- wenn
- wenn und der Operator
Ich kürze jede gültige Variable mit ab und beweise die Gültigkeit von innen nach außen mit Hinweisen auf die jeweiligen Bedingungen die dabei erfüllt werden
b)
Schrittweise Berechnung des Wertes
Ich berechne erneut nach dem oberen Muster von innen nach außen:
c)
Wahrheitstafel der Formel
https://tuwien2020.github.io/tgi-pages/#/truth-table?input=((a+or+!b)+=>+c )+%3C=%3E+((b+=%3E+c)+or+!a)
(Wahrheitsbelegung = Interpretation)
- gültig wenn für alle Wahrheitsb. immer
- erfüllbar wenn für mindestens eine Wahrheitsb.
- widerlegbar wenn für mindestens eine Wahrheitsb.
- unerfüllbar wenn für alle Wahrheitsb. immer
Diese Formel ist erfüllbar und widerlegbar, dadurch aber ungültig und unerfüllbar.

✅ Aufgabe 6
Zeigen Sie, dass die beiden Formeln äqvalent sind.
a)
Wahrheitstafel
https://tuwien2020.github.io/tgi-pages/#/truth-table?input=(!((P+and+Q)+=>+(not+P+<=>+Q) ))+%3C=%3E+(((Q+%3C=%3E+R)+=%3E+P)+and+not(P+nand+Q))
b)
Algebraische Umformungen
Wir wollen algebraisch beweisen, dass dieser Ausdruck immer bzw ergibt.
Kontrolle: https://tuwien2020.github.io/tgi-pages/#/truth-table?input=(!((P+and+Q)+=>+(not+P+<=>+Q) ))+%3C=%3E+(((Q+%3C=%3E+R)+=%3E+P)+and+P+and+Q)
weil
Kontrolle: https://tuwien2020.github.io/tgi-pages/#/truth-table?input=((P+and+Q)+=>+(not+P+<=>+Q) )+or+(((Q+%3C=%3E+R)+=%3E+P)+and+P+and+Q)
Jetzt müsste nur eines der beiden Teile der Funktion sein damit die gesamte Gleichtung immer liefert.
Teil 1:
weil
weil
In allen cases außer
Das bedeutet Teil 2 muss zumindest für diese Interpretation gültig sein damit der gesamte Ausdruck gültig ist.
Teil 2:
Wir setzen die Wahrheitsbelegung für und ein.
Case 1:
Case 2:
✅ Aufgabe 7
Wenn ich schuldig bin, muss ich bestraft werden. [...]
Sokrates ist schuldig.
Sokrates muss bestraft werden.
Wenn Äqiuvalenz gemeint ist ( )
Wenn Implikation gemeint ist ( )
a)
... Ich bin schuldig.
Wenn
- dann ist nur wahr wenn also muss Sokrates bestraft werden
- dann kann auch wahr sein wenn also ist es unklar ob Sokrates bestraft werden muss.
b)
... Ich muss bestraft werden
Wenn
- dann ist nur wahr wenn also ist er schuldig.
- dann kann auch wahr sein wenn also ist es unklar ob er schuldig ist oder nicht.
Konsequenzbeziehung (logische Konseqzenz)
Die Semantik (in der Aussagenlogik) ist durchausdrückbar .
- Aus folgt
- "Falls in der Wahrheitsbelegung alle Prämissen wahr sind, dann ist auch die Konklusion wahr in ." (Kriterium für die Gültigkeit von Inferenzregeln)
- "Die Formel ist eine logische Konsequenz der Formeln "
genau dann wenn
und weil :
genau dann wenn .
In diesem Fall würde die Gültigkeit / Ungültigkeit der Formel ( ) bzw ( ) wenn man alle möglichen Fälle kennt und Wissen über die Realität von Sokrates hat ermitteln können ob Sokrates' Schlussfolgerungen per se Gültigkeit haben oder nicht.
✅ Aufgabe 8
Definition von DNF und KNF der Funktion .
Konj. / Disj. einer Menge von Variablen:
Wir haben eine Funktion mit
- Variablen die durch Interpretation belegt werden
- Abbildung
Definition DNF
Charakteristisches Konjunkt für :
Wobeidie Variablen sind die als Argumente der Funktion dienen.
Beispiel:
Für Wahrheitsbelegung hat den Wert und sonst .
Die Konjunkte werden disjunktiv verbunden.
Dadurch repräsentiert die DNF die Funktion f.
Definition KNF
Charakteristisches Disjunkt für :
Wobeidie Variablen sind die als Argumente der Funktion dienen.
Beispiel:
Für Wahrheitsbelegung hat den Wert und sonst .
Die Konjunkte werden disjunktiv verbunden.
Dadurch repräsentiert die DNF die Funktion f.
Disjunktive Normalform
Konjunktive Normalform
✅ Aufgabe 9
https://tuwien2020.github.io/tgi-pages/#/truth-table?input=(((G+or+!F)+=>+H )+or+(!F+=%3E+G))
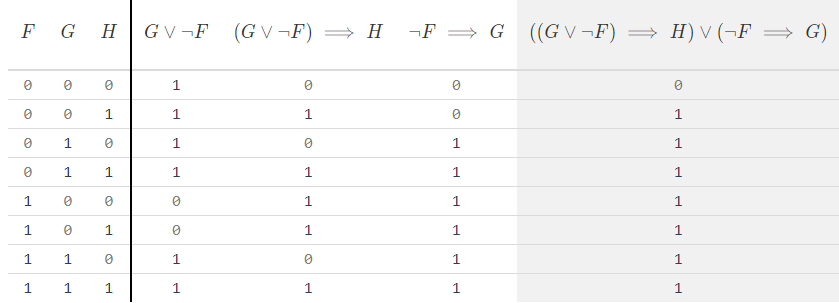
Semantisch zur DNF gelangen:
https://www.wolframalpha.com/input/?i=DNF+(((G+||+~F)+implies+H)+||+(~F+implies+G))
Minimale Form:
Algebraisch zur KNF gelangen:
weil
weil
weil
✅ Aufgabe 10
"Mein lieber Watson, meine intensiven Nachforschungen gestatten mir, folgende Schlüsse zu ziehen:
- Wenn sich Brown oder Cooper als Täter herausstellen sollte, dann ist Adams unschuldig.
- Ist aber Adams oder Cooper unschuldig, dann muss Brown ein Täter sein.
- Ist Cooper schuldig, dann wäre Adams Mittäter."
Adam ist schuldig / der Täter
Brown ist schuldig / der Täter
Cooper ist schuldig / der Täter
Deklarierte Constraints die alle gültig sein müssen:
-
-
-
Wir suchen eine Interpretation für die gültig ist.
Wir vereinfachen und dadurch dass äquivalent zu ist.
-
- weil
Wir suchen also dadurch eine Interpretation für die immer gültig ist.
Dadurch, dass und nicht gleichzeitig sein können, folgt, daraus:
es kann nur gültig sein.
Wir erinnern uns an .
Also lautet die Lösung
Das bedeutet auf die "Wirklichkeit" übertragen:
Es kann nur Brown schuldig sein - Adam und Cooper sind unschuldig.
Überprüfung mit Wahrheitstabelle:
https://tuwien2020.github.io/tgi-pages/#/truth-table?input=((B+or+C)+implies+!A )+and+(!(A+or+C)+implies+B)+and+(C+%3C=%3E+A)
✅ Aufgabe 11
Professor John Frink organisiert eine internationale Konferenz und sucht zur Unterstützung Student Volunteers.
Nach zahlreichen Vorstellungsgesprächen schränkt er die Auswahl auf Bart, Janey, Lisa, Milhouse und Richard ein,
wobei allerdings nur Lisa und Richard auch Fremdsprachen beherrschen.
Er stellt folgende Überlegungen an:
- Janey möchte ich auf jeden Fall, sie hat bei der letzten Konferenz schon erfolgreich mitgearbeitet.
- Ich kann höchstens drei Volunteers anstellen.
- Ich brauche jedenfalls mindestens einen Volunteer, der Fremdsprachen spricht.
- Richard und Milhouse kennen die Räume, in denen die Konferenz stattfinden soll. Einen der beiden sollte ich auf jeden Fall nehmen, aber beide zu nehmen ist nicht notwendig.
- Richard will nur mitmachen, wenn ich auch Bart anstelle.
- Milhouse und Lisa wollen nur gemeinsam genommen werden, da sie andernfalls zusammen auf Urlaub fahren wollen.
Variablen
Bart wird vom Professor angestellt.
Janey wird vom Professor angestellt.
Lisa wird vom Professor angestellt.
Milhouse wird vom Professor angestellt.
Richart wird vom Professor angestellt.
Formeln
Die folgenden contraints müssen in unserer deklarativen Modellierung eingehalten werden - also alle diese Formeln müssen bei der Interpretation nach der wir suchen sein.
- Janey muss mit
- Höchstens 3
- Min. 1 Fremdsprachler
- Entweder Richard oder Milhouse
- Richard nur mit Bart
- Milhouse nur mit Lisa
Algebraische Lösung
Zuerst lösen nutzen wir die Äquivalenzen um alle Formeln zu vereinfachen und setzen überall auf .
steht für Richard und Bart zugleich
steht für Milhouse und Lisa zugleich
- Höchstens 3
- Min. 1 Fremdsprachler
- Entweder Richard oder Milhouse
wir vereinfachen weiter
-
- Min. 1 Fremdsprachler
- Entweder Richard oder Milhouse
Alle deklarierten constraints gemeinsam:
Das lässt sich weiter vereinfachen da:
Es gibt 2 mögliche Interpretationen die alle constraints erfüllen.
Lösung übertragen auf die "Wirklichkeit"
Daraus folgt, dass der Professor unbedingt Lisa mitnimmt und zwischen Team und Team entscheiden muss.
Er könnte dafür beispielsweise eine faire Münze werfen.
✅ Aufgabe 12
Eine Kollegin und ich modellieren das gleiche Problem.
- Sie hat die Formel
- Ich habe die Formeln
- Unsere Formeln sehen unterschiedlich aus.
Überprüfung der semantischen Äquivalenz mit SAT-Solver
- Automatisiert die Formel und die Formel in die oder umwandeln
- in den SAT-Solver eingeben
-
Falls der SAT-Solver in der Lage ist eine Interpretation zu finden mit der die Gleichung aus dem zweiten Schritt nicht erfüllbar ist
(also die Gleichung zu widerlegen) können wir sicher sein, dass die Gleichungen nicht äquivalent sind.
Die einzige Möglichkeit aber die Äquivalenz zu beweisen wäre es alle möglichen Interpretationen durchzugehen.
Was bedeutet es, wenn der SAT-Solver eine erfüllende Variablenbelegung findet?
Eine erfüllende Variablenbelegung für oder wäre eine Lösung unseres Problems → Eine Lösung die sich an alle deklarierten constraints hält.
✅ Aufgabe 13
Gegeben sei:
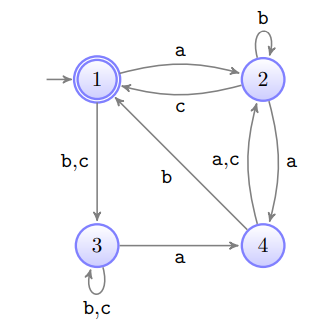
Dieser Automat ist ein DEA: von jedem Zustand gibt es einen eindeutigen Nachfolger mit jeder Eingabe aus dem Alphabet
a)
Alle Wörter aus maximal 3 Zeichen die akzeptiert werden (mit denen der Automat in einem final state ) endet.
-
-
-
-
-
-
b)
Erweiterte Übergangsfunktion (auch für Sätze)
Dieses Wort ist Teil der akzeptierten Sprache
c)
Dieser Automat ist ein DEA: von jedem Zustand gibt es einen eindeutigen Nachfolger mit jeder Eingabe aus dem Alphabet
transition function
Totale Funktion: Funktion, die für jeden Wert aus Definitonsmenge ein Abbild hat. Deshalb deterministisch.
✅ Aufgabe 14
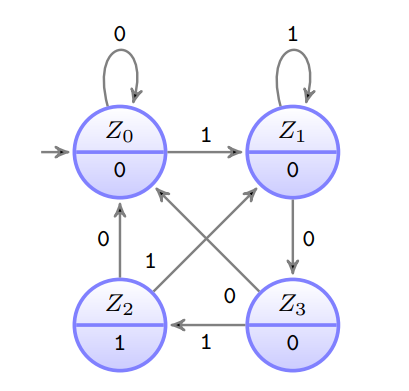
a)
b)
Erweiterte Ausgabefunktion (auch für Sätze)
c)
Übersetzungsfunktion (gleich wie Mealy)
✅ Aufgabe 15
Elektronisches Tresorschloss
Display:
darstellbar
2 Stellen
initial: , linke stelle aktiv
Tasten:
Es gibt immer eine aktive Stelle
inkrementiert aktive Ziffer (ab 2 → 0)
aktive Stelle ist links (looped nicht im kreis)
aktive Stelle ist rechts (looped nicht im kreis)
Wenn 21 eingegeben und gedrückt dann öffnet sich Tresor. (alle Tasten außerdann ignoriert)
Ansonsten nachdem gedrückt wurde in einem Fehlerzustand. (alle Tasten außerdann ignoriert)
Kann immer gedrückt werden → setzt zurück in den Anfangszustand
Modellierung eines endlichen Automaten
a)
Welche Informationen sind notwendig um den Zustand des Schlosses zu beschreiben?
Notwendige Informationen / Zustände:
- Zahlen am Display (also ein Wert für jede Stelle)
- Aktive Stelle
- Ob gerade der Tresor geöffnet wurde oder in einem Fehlerzustand ist
Wie viele Zustände kann das Schloss annehmen?
-
-
- Mögliche Zahlenkombinationen bei denen je eine Stelle aktiv ist
Wie viele Zustände kann das Schloss im Allgemeinen mitnZiffern (statt 3) undkStellen (statt 2) annehmen?
-
Anzahl der möglichen aktiven Stellen Anzahl der Ziffer hoch Stellen.
b)
Welche Aktionen führen zu einem Zustandswechsel?
Jeder Tastendruck - siehe oben.
c)
Geben Sie einen endlichen Automaten an, der das Verhalten des beschr. Schlosses vollständig beschreibt. (Auswahl zwischen Tabelle und Graph möglich)
( sind alle Kombinationen die den Tresor öffnen)
Grobe Skizze:
Die Idee besteht daraus unseren Graphen in Gebiete zu unterteilen.
Links sind alle Zahlenkombinationen, wobei immer nur die linke Zahl aktiv ist und man weiß dass jede Aktion nur einen Einfluss auf dieses Gebiet haben wird und rechts vice versa.
Weiters weiß man dass ein Wechsel zwischen den beiden Gebieten links und rechts nur mit bzw möglich ist.
Beim drücken von führt nur ein Zustand zu und alle anderen zum Zustand .
ist meine Falle, deshalb werde ich nicht alle Kanten dazu einzeichnen (zur besseren Lesbarkeit).
Weiters führt das Drücken von immer wieder zum Zustand weshalb man diese theoretisch auch nicht einzeichnen bräuchte.
Vollständige Version: