see📎
Matrix-Vector multiplication
for detailed explaination
(adbecf)⋅(gikhjl)=(gh)⋅(ad)+(ij)⋅(be)+(kl)⋅(cf)
Sequential solution in
O(n³)
Assume
A,B,C
are
n×n
matrices.
and also
n≫p,p∣n
MPI processes organised into
p×p
matrices through
MPI_Cart_create
.
Each process
(i,j)
contains submatrices
A′,B′,C′
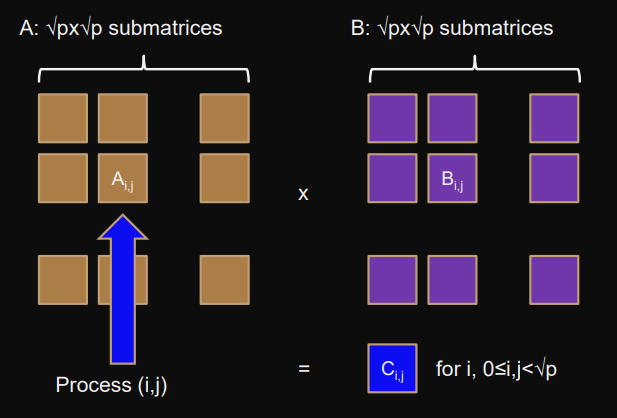
There are
p
communicators for rows
p
communicators for columns
Folklore: Blockwise algorithm
Analysis
Work:
O(n3/p+n2/p)
Communication:
2⋅(
lo
g2(p)⋅α+β⋅(p−1)⋅n2/p)
Space:
p⋅n²
very inefficient - increases by factor
p
over sequential algorithm
Speedup:
p
when
p∈O(n2)
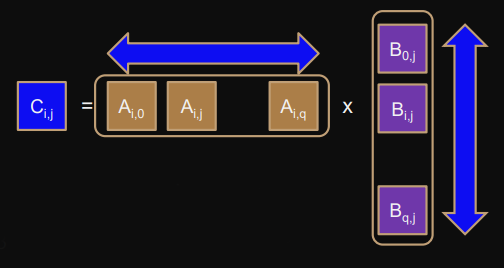
q=p
Process
(i,j)
computes
Ci
j
′=(Ai,0′,Ai,1′,…Ai,q′)⋅(B0,j′,B1,j′,…,Bq,j′)
Algorithm
-
Get data
AllgatherAi,∗
on rows
AllgatherA∗,
j
on columns
-
Locally compute (sequentially)
Ci,
j
=
∑
1=0p−1Ai,1⋅B1,
j
Scalable Universal Matrix-Multiplication Algorithm (SUMMA)
Analysis
Work:
O(n3/p+n2/p)
Communication:
2⋅p⋅(
lo
g2(p)⋅α+β⋅n2/p)
Space:
2⋅n²/p
Speedup:
p
when
p∈O(n2)
Idea: Pipelining
Allgather
operations
Ci,j
gets computed in
p
communication rounds.
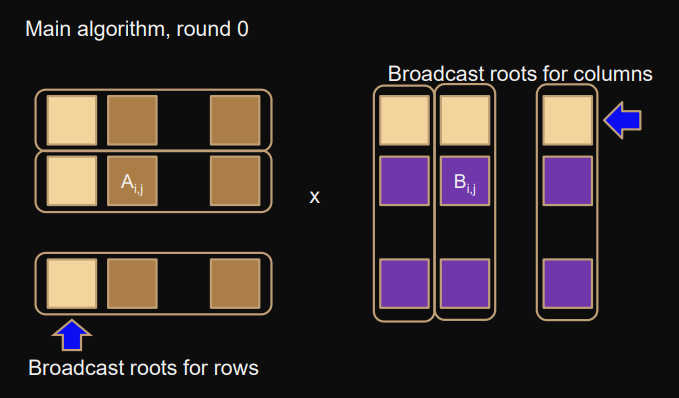
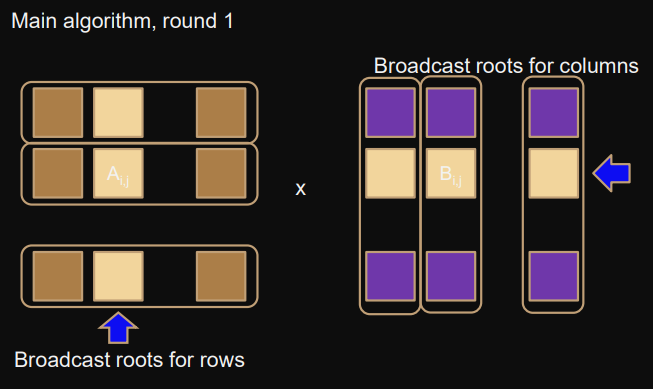
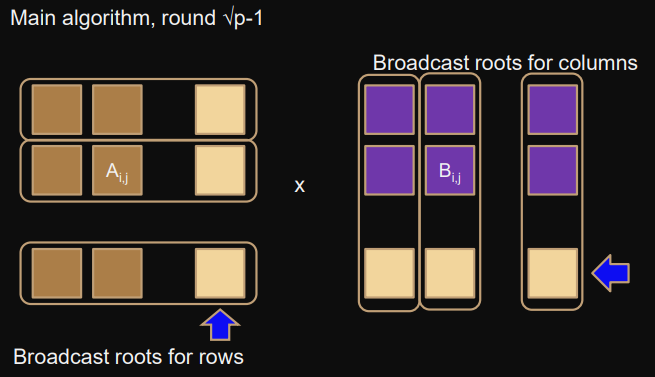
Main algorithm
In round
l∈[0;p−1]
we
-
broadcoast
Ai,1
in the row communicator
-
broadcoast
Bi,
j
in the column communicator
-
Update
C += A⋅B