Entscheidbarkeit

Turingmaschinen

💡

Turingmaschine hält immer, wenn sie ein Wort akzeptiert (wenn mit dem Wort ein Endzustand erreicht wird)

$\small w \in \mathcal L(M) \Rarr$ Anhalten

Entscheidbarkeit

Entscheidbarkeit = Frage ob Problem / Sprache rekursiv ist

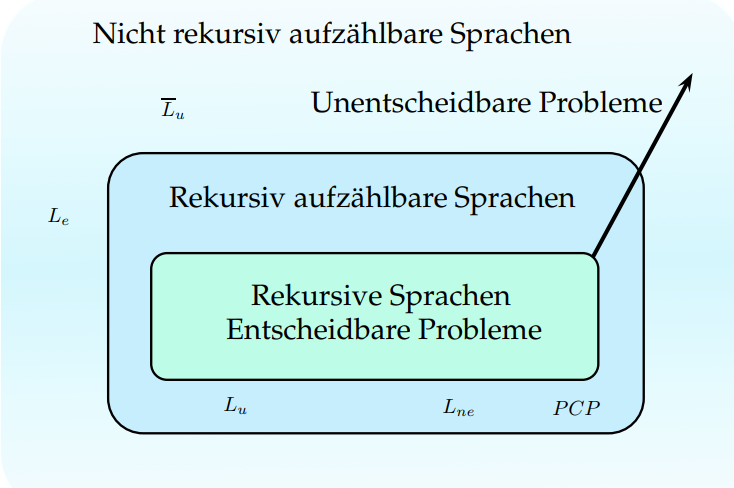
Rekursive Sprachen

Wenn $\exists$ deterministische Turingmaschine, die diese Sprache akzeptiert -

und bei anderen Sprachen auch immer hält.

entscheidbare bzw. rekursiv entscheidbare Probleme / Sprachen

Die Turingmaschineentscheidetdie Sprache.

Wenn $\exists$ deterministische Turingmaschine, die uns bei Problemen "ja" oder "nein" antworten kann. Sie hält immer, wir schauen nur ob ein Endzustand erreicht wurde oder nicht.

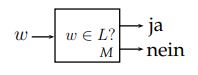
Rekursiv-aufzählbare Sprache

$\small w \in L(M) \Longleftrightarrow(M, w) \in L_{u}$

Wenn $\exists$ deterministische Turingmaschine, die diese Sprache akzeptiert -

und bei anderen Sprachen möglicherweise nicht hält.

recursively-enumerable, semi-decidable, turing-recognizable

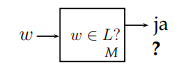
Nicht-rekursiv-aufzählbare Sprachen

Wir wollen beweisen, dass es Sprachen gibt die nicht rekursiv aufzählbar sind.

Codierung von Turingmaschinen (Voraussetzung für Beweis)

Man kann eine Turingmaschine zu einem String umwandeln:

$M=\left(\left\{q_{1}, q_{2}, \ldots, q_{r}\right\},\{0,1\},\left\{0,1, B, X_{4}, \ldots, X_{s}\right\}, \delta, q_{1}, B,\left\{q_{2}\right\}\right)$

Einzelne Abbildungen der Übergangsfunktion:

$\delta\left(q_{i}, X_{j}\right)=\left(q_{k}, X_{l}, D_{m}\right) \longmapsto 0^{i} 10^{j} 10^{k} 10^{l} 10^{m}$ (Es werden nur 0er potenziert)

Man setzt bestimmte Anzahl an Nullern um den Index für $\small i, j,k,l,m$ zu definieren und trennt die Nuller mit einsen.

Dann trennt man alle diese Strings mit "11" und listet dadurch alle möglichen Abbildungen auf.

Beweis

Eine Sprache $L \in \mathcal{P}\left(\Sigma^{*}\right)$ über $\Sigma=\{0,1\}$ ist genau dann rekursiv-aufzählbar wenn es eine deterministische Turingmaschine gibt die immer nur diese akzeptiert und keine andere.
$\mathcal{P}\left(\Sigma^{*}\right)$ ist überabzählbar

$M \in \Sigma^{*}$ : Jede Turingmaschine $M$ kann selbst mit $\Sigma$ codiert werden.
$\Sigma^{*}$ ist abzählbar

Daraus folgt: Es gibt also überabzählbar viele Sprachen, von denen jedoch nur abzählbar viele von einer Turingmaschine akzeptiert werden.

Sätze

Church-Turing-These

Es gibt keine anderen Modelle die mehr formale Sprachen als Turingmaschinen akzeptieren können. (Bisher nicht widerlegt)

Quasi: Turingmaschinen können alles berechnen was berechenbar ist.

Wenn $L$ rekursiv ist, ist auch $\bar L$ rekursiv

Man antwortet mit der Negation von der ursprünglichen Antwort.

Wenn sowohl $L$ als auch $\bar L$ rekursiv-aufzählbar sind, sind sie beide dadurch rekursiv

Die "ja" antwort des Komplements, ist die "nein" Antwort der ursprünglichen Sprache.

Es kann nur eines gelten:

$L$ und $\bar L$ sind beide rekursiv

$L$ und $\bar L$ sind beide nicht-rekursiv-aufzählbar (außerhalb der Menge der rekusiv-aufzählbaren Sprachen)

Eines der beiden ist rekursiv-aufzählbar (aber nicht rekursiv) und das andere nicht-rekursiv-aufzählbar

Halteproblem

💡

Wir nehmen zur Vereinfachung an, dass

M

nur hält wenn es einen Endzustand erreicht - also wenn

\small w \in L(M)

(Es könnte sonst auch halten ohne in einen Endzustand zu kommen)

Das Halteproblem

$L_{u}=\{(M, w) \mid M \text { akzeptiert } w\}$

Das Halteproblem ist eine Sprache, bestehend aus $\small (M, w)$ Tupeln bei denen gilt, dass $M$ das Wort $w$ akzeptiert, also $\small w \in L(M)$ .

Das Halteproblem ist rekursiv-aufzählbar aber nicht rekursiv .

$L_u$ ist rekursiv-aufzählbar

Es gibt universelle Turingmaschinen die mit Code und Input ein Verhalten simulieren können.

Universelle Turingmaschine $U$ nimmt Maschinencode $M$ und $w$ und hält genau dann, wenn es $M$ tun würde.

$\small U \text { akzeptiert }(M, w) \Longleftrightarrow M \text { akzeptiert } w \Longleftrightarrow(M, w) \in L_{u}$

$\small (M, w) \in L(U)\Longleftrightarrow w \in L(M) \Longleftrightarrow(M, w) \in L_{u}$

$L_u$ ist nicht rekursiv

Indirekter Beweis

Angenommen $\exists$ Maschine $H$ die immer hält und dadurch ist $L_u$ rekursiv:

$\small H(M, w)= \begin{cases}\text { ja } & M \text { hält bei } w \\ \text { nein } & M \text { hält nicht bei } w\end{cases}$

Ja und Nein beziehen sich darauf, ob $(M, w)\in L_u$ und ob $H$ einen Endzustand erreicht, aber $H$ hält immer.

Dann $\exists$ Maschine $D$ die das Gegenteil von dem macht was $M$ machen würde:

$\small D(M,w) = \begin{cases}\text { halten} & \text { wenn } H \text { nein ausgibt} \\ \text { nicht halten} & \text { wenn } H \text { ja ausgibt } \end{cases}$

Man könnte jedes beliebige Wort $w$ nutzen - aber wir wollen, dass $D$ nur eine Eingabe hat - den Code der Maschine: $\small D(M_{\text{code}}) = D(M, M_{\text{code}})$

$\small D(M_{\text{code}}) = \begin{cases}\text { halten} & M \text { hält nicht bei } M_{\text{code}} \text { laut } H\\ \text { nicht halten } & M \text { hält bei } M_{\text{code}} \text { laut } H\end{cases}$

Wir setzen $D_{\text{code}}$ als Argument für $D$ ein:

$\small D(D_{\text{code}}) = \begin{cases}\text { halten} & D \text { hält nicht bei } D_{\text{code}} \text { laut } H\\ \text { nicht halten } & D \text { hält bei } D_{\text{code}} \text { laut } H\end{cases}$

Paradoxon: Dadurch verhält sich $D$ immer gegensätzlich zu dem wie es der Haltealgorithmus $H$ vorausgesagt hat.

$\overline{L_{u}}$ ist nicht rekursiv-aufzählbar

$\overline{L_{u}}=\{(M, w) \mid M \text { akzeptiert } w \text { nicht}\}$

Angenommen $\overline{L_{u}}$ wäre auch rekursiv aufzählbar, dann wären sie dadurch gemeinsam rekursiv.

Berechenbarkeit

💡

Vorsicht: berechenbar nicht mit entscheidbar (rekursiv) verwechseln

Partiell berechenbar

Wenn für $f: \Sigma^{*} \longmapsto \Sigma^{*}$ eine Turingmaschine $M_f$ existiert, sodass $\forall x \in \Sigma^*$

Wenn $f(x)$ definiert ist, dann hält $M_f$
wenn es mit $x$ startet und schreibt $f(x)$ auf das Band.

Wenn $f(x)$ nicht definiert ist, dann hält $M_f$ nicht
wenn es mit $x$ startet.

Total berechenbar

Wenn für alle $x\in \Sigma^*$ $f(x)$ definiert ist und $f$ partiell berechenbar ist.

Reduktion von Sprachen

Reduktion $A \leq B$

$A \sube \Sigma^*$ lässt sich auf $B \sube \Gamma^*$ reduzieren wenn es eine total berechenbare Funktion

$f: \Sigma^{*} \longmapsto \Gamma^{*}$ gibt, sodass $\forall w \in \Sigma^* : ~ f(w)\in B \Rarr w\in A$

Reduktion nutzen für Beweise

Angenommen $A \leq B$ :

$A$ nicht rekursiv $\Rarr$ $B$ nicht rekursiv

$A$ nicht rekursiv-aufzählbar $\Rarr$ $B$ nicht-rekursiv-aufzählbar

$B$ rekursiv $\Rarr$ $A$ rekursiv

$B$ rekursiv-aufzählbar $\Rarr$ $A$ rekursiv-aufzählbar

Beispiel

$\small L_{e}=\{M_{\text{code}} \mid L(M_{\text{code}})=\{\} ~\}$ Sprache aus allen Codes die nur empty akzeptieren

$\small L_{ne}=\{M_{\text{code}} \mid L(M_{\text{code}})\neq \{\} ~\}$ Sprache aus allen Codes die nicht empty akzeptieren

$L_{ne}$ ist rekursiv-aufzählbar

$M$ (nicht-deterministisch) nützt die universelle Maschine $U$ mit den Eingaben: $M_i$ und ein random Wort $w$ .

Die universelle Maschine simuliert $M_i$ mit der Eingabe $w$ .

Wenn $U$ akzeptiert $\Rarr L(M_i) \neq \{\}$

$L_{ne}$ ist nicht rekursiv

$L_u \leq L_{ne}$

Wir reduzieren das Halteproblem auf das Nonempty-Problem:

Angenommen $\exists H: L(H) = L_u$
Wenn $(M, w)$ von $H$ akzeptiert wird, dann bedeutet das, dass $M$ mit $w$ hält.

Daraus folgt $\exists M': (M',w) \in L(H) \Leftrightarrow L\left(M^{\prime}\right) \neq\{\}$
Wenn $M'$ das wort $w$ akzeptiert, dann kann die Sprache $L(M')$ nicht $\{\}$ sein.

Dadurch, dass wir wissen dass $H$ existiert, daber nicht rekursiv ist, folgt daraus, dass $L_{ne}$ auch nicht rekursiv ist.

Eigenschaft

Eine Eigenschaft ist eine Teilmenge $P$ von allen rekursiv-aufzählbaren Sprachen (über ein Alphabet).

Eine Teilmenge aller möglichen rek-aufzählbaren Sprachen über das Alphabet.

Beispiele
Die folgenden Eigenschaften treffen auf die rekursiv-aufzählbare Sprache $L=\{a, b\}^*$ zu ( $L$ ist ein Element dieser Eigenschaften - also $\small L \in P$ )
$\small P_{}=\left\{L \mid L=L^{*}\right\}$ (da der Sternoperator idempotent ist)
$\small P_{}=\{L \mid L \text { ist rekursiv-aufzählbar }\}$
$\small P_{}=\{L \mid L \text { ist rekursiv }\}$
Aber nicht die Eigenschaften (keine möglichen Teilmengen)
$\small P_{}=\{L \mid L \text { ist endlich }\}$
$\small P_{}=\{\{\varepsilon\}\}$
$\small P_{}=\{\}$

Triviale Eigenschaften

$\small P_{}=\{\}$

ist von keiner rekursiv-aufzählbaren Sprache die Teilmenge

Die Eigenschaft $\small P_{}=\{\}$ (keine Sprache) ist nicht dasselbe wie die Eigenschaft $\small P=\{\{\}\}$ (diese trifft zb auf die Leer-Sprache zu)

$\small P_{}=\{L \mid L \text { ist rekursiv-aufzählbar }\}$

ist von jeder rekursiv-aufzählbaren Sprache die Teilmenge

Satz von Rice

Sagt ob eine Eigenschaft (Sprachenmenge) rekursiv ist.

Wie kann eine Menge an Sprachen rekursiv sein?

$P$ ist rekursiv wenn es für $L_P$ eine deterministische Turingmaschine gibt:

$L_P =$ Die Menge aller Maschinen-Codes, die eine Sprache aus Menge $P$ akzeptieren.

$L_{P}=\left\{M_{\text{code}} \mid L\left(M_{\text{code}}\right) \in P\right\}$

Satz von Rice

Eigenschaft nicht trivial $\Rarr$ Eigenschaft nicht rekursiv

Beispiele
1) $P=\{L \mid ~~|L| \geq 7\}$
Sprache mit 7 oder mehr Elementen
Maschine die nur Sprachen mit mehr als 7 Wörtern akzeptiert
Beweis: (für nicht Trivialität)
$\exists$ rekursiv-aufzählbare Sprache mit dieser Teilmenge $L_{1}=\left\{a, a^{2}, a^{3}, \ldots, a^{7}\right\}$
$\exists$ rekursiv-aufzählbare Sprache ohne dieser Teilmenge: $L_{2}=\{\}$
2) $\small P_{}=\{L \mid L \text { ist eine reguläre Sprache}\}$
Maschine die nur reguläre Sprache akzeptiert
Beweis:
$\exists$ rekursiv-aufzählbare Sprache mit dieser Teilmenge $L_{1}=\left\{a, b\right\}^*$
$\exists$ rekursiv-aufzählbare Sprache ohne dieser Teilmenge $L_{u}$

Fällen wo Anwendung von Satz von Rice ungültig ist

Satz ausgenommen: Es handelt sich nicht um eine Bedingung der akzeptierten Sprache der Turingmaschine sondern um eine Bedingung der Turingmaschine selbst.

Beispiele
1) $\small P=\{M_i \mid M_i ~\text{hat} \geq 7 \text{ Zustände} \}$
Bezieht sich auf Maschine und nicht Sprache
2) $\small P=\{M_i \mid M_i ~\text{akzeptiert rekursiv aufzählbare Sprache} \}$
Ist für jede rekursiv-aufzählbare Sprache erfüllt.

Beispiel: Nicht-rekursive Probleme

Postsches Korrespondenz Problem $\small \text{PCP}$ : Rekursiv-aufzählbar, nicht rekursiv

Gegeben

$A$ - Alphabet

$k\in \N$

$\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{k}, y_{k}\right)$ - Folge von Wortpaaren

wobei $x_{i}, y_{i} \in A^{+}$ für $1 \leq i \leq k$

Frage

$\exists$ Folge von Indizes $i_{1}, i_{2}, \ldots, i_{n \leq k}$ für die Paare, sodass gillt:

$x_{i_{1}} x_{i_{2}} \ldots x_{i_{n}}=y_{i_{1}} y_{i_{2}} \ldots y_{i_{n}}$

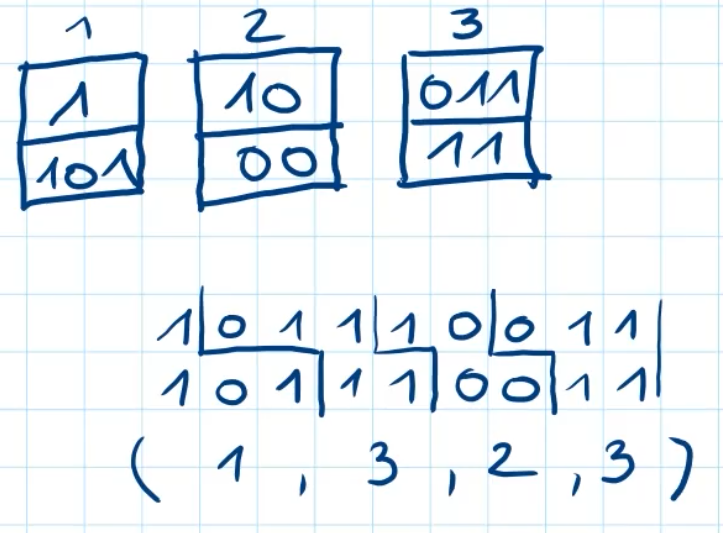
10. Hilbertsches Problem: nicht rekursiv

Gegeben

$n \in \mathbb{N}$

Polynom $p\left(x_{1}, \ldots, x_{n}\right)$

Frage

Besitzt $p$ ganzzahlige Nullstellen?