Link zur Web Version: https://www.notion.so/AB2-53ebe76b45bf4af9b8f4d4c1d23d4946
Aufgabe 1 ∑ \sum ∑
ε \varepsilon ε (equivalent zum Leer-String ≠ Leerzeichen ␣ ␣ ␣ ≠ leere Menge )
w w w Σ \Sigma Σ
Verkettung:
w ⋅ w ′ = w w ′ w \cdot w' = ww' w ⋅ w ′ = w w ′
Wort Mengen
∑ + \sum^+ ∑ + ohne ε \varepsilon ε
∑ ∗ \sum^* ∑ ∗ mit ε \varepsilon ε
∑ ω \sum^{\omega} ∑ ω unendlichen
Wörter = "
ω \omega ω
L L L - Formale Sprache über ∑ ∗ \sum^* ∑ ∗
Sprache ist eine Teilmenge aller Wörter des Alphabets potenziert mit Kleene Stern:
L ⊆ Σ ∗ L \subseteq \Sigma^{*} L ⊆ Σ ∗
Angabe ∑ = { d,e,n,o,s } \sum = \{\texttt{d,e,n,o,s}\} ∑ = { d,e,n,o,s }
Die formale Sprache über
∑ ∗ \sum^* ∑ ∗
L ⊆ Σ ∗ L \subseteq \Sigma^{*} L ⊆ Σ ∗ sonne \texttt{sonne} sonne sonde \texttt{sonde} sonde
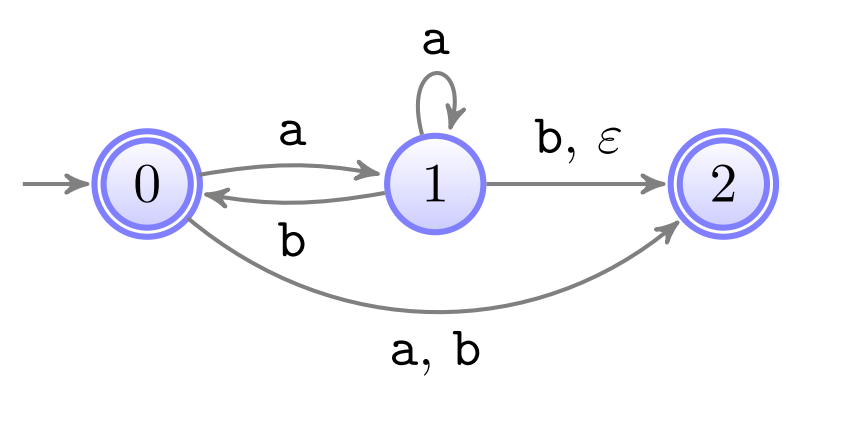
a) Posix Extended Regular Expression L = ˆ [denos]* (sonne | sonde) $ \texttt{L = \^{} [denos]* (sonne | sonde) \$} L = ˆ [denos]* (sonne | sonde) $
b) Nicht deterministischer Automat Die Korrektheit der Modellierung ist unmittelbar einsichtig.
c) Determinisierung Gegeben: NEA
A = ⟨ Q , Σ , δ , q 0 , F ⟩
\mathcal{A}=\left\langle Q, \Sigma, \delta, q_{0}, F\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩ (A steht für Automat)
δ ⊆ Q × ( Σ ∪ { ε } ) × Q
\delta \subseteq Q \times(\Sigma \cup\{\varepsilon\}) \times Q
δ ⊆ Q × ( Σ ∪ { ε }) × Q
Gesucht: DEA
A undefined = ⟨ Q undefined , Σ , δ undefined , q 0 undefined , F undefined ⟩
\widehat{\mathcal{A}}=\left\langle\widehat{Q}, \Sigma, \widehat{\delta}, \widehat{q_{0}},
\widehat{F}\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩
δ undefined : Q undefined × Σ ↦ Q undefined
\widehat{\delta}: \widehat{Q} \times \Sigma \mapsto \widehat{Q}
δ : Q × Σ ↦ Q
unter der Bedingung dass
A ^ \mathcal{\hat{A}} A ^ A \mathcal{A} A
L ( A ) = L ( A undefined )
\mathcal{L}(\mathcal{A})=\mathcal{L}(\widehat{\mathcal{A}})
L ( A ) = L ( A )
Definition von DEA A undefined \mathcal{\widehat{A}} A
Q undefined = 2 Q \widehat{Q}=2^{Q} Q = 2 Q (Potenzmenge von Q Q Q - Alle Teilmengen / Zustands-Wörter)
q 0 undefined = { q 0 } \widehat{q_{0}}=\left\{q_{0}\right\} q 0 = { q 0 } (Klammern stehen nicht für Menge)
F undefined = { { q undefined ∈ Q undefined ∣ q undefined ∩ F ≠ ∅ } ∪ { q 0 undefined } falls ε ∈ L ( A ) { q undefined ∈ Q undefined ∣ q undefined ∩ F ≠ ∅ } sonst
\widehat{F}=\left\{\begin{array}{ll}\{\widehat{q} \in \widehat{Q} \mid \widehat{q} \cap F \neq \emptyset\}
\cup\left\{\widehat{q_{0}}\right\} & \text { falls } \varepsilon \in \mathcal{L}(\mathcal{A})
\\\{\widehat{q} \in \widehat{Q} \mid \widehat{q} \cap F \neq \emptyset\} & \text { sonst
}\end{array}\right.
F = { {
q
∈ Q ∣
q
∩ F = ∅ } ∪ {
q
0
} {
q
∈ Q ∣
q
∩ F = ∅ } falls ε ∈ L ( A ) sonst
Unsere finalen Zustände sind alle Zustands-Wörter / Mengen die bei einem Durchschnitt mit dem Zustand
F F F nicht leer sind → Die den Buchstaben F F F enthalten.
Falls Leerwörter erlaubt sind muss der Anfangszustand auch enthalten sein.
∀ q undefined ∈ Q , s ∈ ∑ : \forall \widehat{q} \in Q, s\in \sum : ∀ q ∈ Q , s ∈ ∑ :
δ undefined ( q undefined , s ) = { q ′ ∈ Q ∣ ∃ q ∈ q undefined , sodass ( q , s , q ′ ) ∈ δ ∗ }
\widehat{\delta}(\widehat{q}, s)=\left\{q^{\prime} \in Q \mid \exists q \in \widehat{q}, \text { sodass
}\left(q, s, q^{\prime}\right) \in \delta^{*}\right\}
δ ( q , s ) = { q ′ ∈ Q ∣ ∃ q ∈ q , sodass ( q , s , q ′ ) ∈ δ ∗ }
bzw
δ undefined ( q undefined , s ) = ⋃ q ∈ q undefined { q ′ ∈ Q ∣ ( q , s , q ′ ) ∈ δ ∗ } = ⋃ q ∈ q undefined δ ∗ ( q , s )
\widehat{\delta}(\widehat{q}, s)=\bigcup_{q \in \widehat{q}}\left\{q^{\prime} \in Q \mid\left(q, s,
q^{\prime}\right) \in \delta^{*}\right\}=\bigcup_{q \in \widehat{q}} \delta^{*}(q, s)
δ ( q , s ) = ⋃ q ∈
q
{ q ′ ∈ Q ∣ ( q , s , q ′ ) ∈ δ ∗ } = ⋃ q ∈
q
δ ∗ ( q , s )
Die Übergangsfunktion:
Q × s ∈ ∑ ↦ { … } Q \times s\in\sum \mapsto \{ \dots\} Q × s ∈ ∑ ↦ { … }
Bildet jeden Zustand mit Symbol auf einem Wort, dass alle Folgezustände enthält.
Dadurch, dass es keine ε \varepsilon ε gibt ist Tabelle von δ \delta δ gleich mit δ ∗ \delta^* δ ∗
Anfangszustand ist
1 1 1 6 6 6
δ ∗ d e n o s 1 { 1 } { 1 } { 1 } { 1 } { 1 , 2 } 2 { } { } { } { 3 } { } 3 { } { } { 4 } { } { } 4 { 6 } { } { 5 } { } { } 5 { } { 7 } { } { } { } 6 { } { 7 } { } { } { } 7 { 7 } { 7 } { 7 } { 7 } { 7 }
\begin{array}{c|ccccc}\delta^{*} & \mathrm{d} & \mathrm{e} & \mathrm{n} & \mathrm{o} &
\mathrm{s} \\\hline 1 & \{1\} & \{1\} & \{1\} & \{1\} & \{1,2\} \\2 & \{\} & \{\}
& \{\} & \{3\} & \{\} \\3 & \{\} & \{\} & \{4\} & \{\} & \{\} \\4 & \{6\}
& \{\} & \{5\} & \{\} & \{\} \\5 & \{\} & \{7\} & \{\} & \{\} & \{\} \\6
& \{\} & \{7\} & \{\} & \{\} & \{\} \\7 & \{7\} & \{7\} & \{7\} & \{7\}
& \{7\}\end{array}
δ
∗ 1 2 3 4 5 6 7 d { 1 } { } { } { 6 } { } { } { 7 } e { 1 } { } { } { } { 7 } { 7 } { 7 } n { 1 } { } { 4 } { 5 } { } { } { 7 } o { 1 } { 3 } { } { } { } { } { 7 } s { 1 , 2 } { } { } { } { } { } { 7 }
Wir definieren eine
δ undefined \widehat{\delta} δ
Anfangszustand ist
1 1 1 1 1 1 7 7 7
Wichtig: die Tabelleneinträge sind keine Mengen sondern Zustands-Wörter obwohl wir {} benutzen.
δ undefined d e n o s { 1 } { 1 } { 1 } { 1 } { 1 } { 1 , 2 } { 1 , 2 } { 1 } { 1 } { 1 } { 1 , 3 } { 1 } { 1 , 3 } { 1 } { 1 } { 1 , 4 } { 1 } { 1 } { 1 , 4 } { 1 , 6 } { 1 } { 1 , 5 } { 1 } { 1 } { 1 , 5 } { 1 } { 1 , 7 } { 1 } { 1 } { 1 } { 1 , 6 } { 1 } { 1 , 7 } { 1 } { 1 } { 1 } { 1 , 7 } { 1 , 7 } { 1 , 7 } { 1 , 7 } { 1 , 7 } { 1 , 7 }
\begin{array}{c|ccccc}\widehat{\delta} & \mathrm{d} & \mathrm{e} & \mathrm{n} & \mathrm{o} &
\mathrm{s} \\\hline\{1\} & \{1\} & \{1\} & \{1\} & \{1\} & \{1,2\} \\\{1,2\} & \{1\}
& \{1\} & \{1\} & \{1,3\} & \{1\} \\\{1,3\} & \{1\} & \{1\} & \{1,4\} & \{1\}
& \{1\} \\\{1,4\} & \{1,6\} & \{1\} & \{1,5\} & \{1\} & \{1\} \\\{1,5\} & \{1\}
& \{1,7\} & \{1\} & \{1\} & \{1\} \\\{1,6\} & \{1\} & \{1,7\} & \{1\} & \{1\}
& \{1\} \\\{1,7\} & \{1,7\} & \{1,7\} & \{1,7\} & \{1,7\} & \{1,7\} \end{array}
δ
{ 1 } { 1 , 2 } { 1 , 3 } { 1 , 4 } { 1 , 5 } { 1 , 6 } { 1 , 7 } d { 1 } { 1 } { 1 } { 1 , 6 } { 1 } { 1 } { 1 , 7 } e { 1 } { 1 } { 1 } { 1 } { 1 , 7 } { 1 , 7 } { 1 , 7 } n { 1 } { 1 } { 1 , 4 } { 1 , 5 } { 1 } { 1 } { 1 , 7 } o { 1 } { 1 , 3 } { 1 } { 1 } { 1 } { 1 } { 1 , 7 } s { 1 , 2 } { 1 } { 1 } { 1 } { 1 } { 1 } { 1 , 7 }
F undefined = { { 1 , 7 } } \widehat{F}=\{\{1, 7\}\} F = {{ 1 , 7 }}
Q undefined = { { 1 } , { 1 , 2 } , { 1 , 3 } , { 1 , 4 } , { 1 , 5 } , { 1 , 6 } , { 1 , 7 } }
\widehat{Q}=\{\{1\},\{1,2\},\{1,3\},\{1,4\},\{1,5\},\{1,6\},\{1,7\}\}
Q = {{ 1 } , { 1 , 2 } , { 1 , 3 } , { 1 , 4 } , { 1 , 5 } , { 1 , 6 } , { 1 , 7 }}
Aufgabe 2
Algebraische Notation
→ \rarr →
Um Klammern auszulassen - Stärke der Bindung:
Kleene Stern Verkettung Vereinigung
a) a b ∗ b + ( b a ) ∗ = ( a ( b ∗ ) b ) + ( ( b a ) ∗ ) ab^*b+(ba)^* = (a(b^*)b)+((ba)^*) a b ∗ b + ( ba ) ∗ = ( a ( b ∗ ) b ) + (( ba ) ∗ )
b) ( a + c b ∗ ) c c ∗ = ( a + c ( b ∗ ) ) c ( c ∗ ) (a +cb^*)cc^* = (a + c(b^*))c(c^*) ( a + c b ∗ ) c c ∗ = ( a + c ( b ∗ )) c ( c ∗ )
Aufgabe 3 Sind diese Gleichungen gültig?
Ja → Begründing
Nein → Gegenbeispiel
a) L ⋅ { } = L ∪ { ε } L \cdot\{\}=L \cup\{\varepsilon\} L ⋅ { } = L ∪ { ε }
Nein. denn das die Leere Menge ist das
Nullelement
bezüglich der Verkettung
( ∀ L : L ⋅ { } = { } ) (\forall L: ~~L \cdot\{\}=\{\}) ( ∀ L : L ⋅ { } = { })
Gegenbeispiel:
{ a , b , c } ∪ { ε } = { a , b , c , ε } ≠ { } = { a , b , c } ⋅ { }
\{a,b,c\}\cup \{\varepsilon\} = \{a,b,c,\varepsilon\} \not = \{\} = \{a,b,c\}\cdot \{\}
{ a , b , c } ∪ { ε } = { a , b , c , ε } = { } = { a , b , c } ⋅ { }
b) L ⋅ { ε } = L ∪ { } L \cdot\{\varepsilon\}=L \cup\{\} L ⋅ { ε } = L ∪ { }
Ja! Denn
{ ε } \{\varepsilon\} { ε } Einselement
bezüglich der Verkettung
( ∀ L : L ⋅ { ε } = L ) (\forall L: ~~L \cdot\{\varepsilon\}=L) ( ∀ L : L ⋅ { ε } = L ) { } \{\} { } ( ∀ L : L ∪ { } = L ) (\forall L: ~~L \cup\{\}=L) ( ∀ L : L ∪ { } = L )
c) { ε } ⋅ L ∗ = L + \{\varepsilon\} \cdot L^{*}=L^{+} { ε } ⋅ L ∗ = L +
Zuerst sei aus Unterbeispiel
b)
festgehalten, dass diese Gleichung gleichzusetzen ist mit:
L ∗ = L + L^{*}=L^{+} L ∗ = L +
Und der Definition zufolge:
L + = ⋃ n ≥ 1 L n L^{+}=\bigcup_{n \geq 1} L^{n} L + = ⋃ n ≥ 1 L n (Alle Wörter der Länge n für n≥1)
L ∗ = ⋃ n ≥ 0 L n = L 0 ∪ L + = { ε } ∪ L +
L^{*}=\bigcup_{n \geq 0} L^{n}=L^{0} \cup L^{+}=\{\varepsilon\} \cup L^{+}
L ∗ = ⋃ n ≥ 0 L n = L 0 ∪ L + = { ε } ∪ L + "Kleene Stern"
Also kann diese Gleichung nicht stimmen.
Gegenbeispiel (aus der Vorlesung):
L = { a , 42 } L=\{\mathrm{a}, 42\} L = { a , 42 }
L 0 = { ε } L^{0}=\{\varepsilon\} L 0 = { ε }
L + = ⋃ n ≥ 1 L n = L 1 ∪ L 2 ∪ L 3 ∪ ⋯ = { a , 42 , aa, a 42 , 42 a , 4242 , aaa, a a 42 , a 42 a , a4242 , 42 a a , … }
\begin{aligned}L^{+} &=\bigcup_{n \geq 1} L^{n}=L^{1} \cup L^{2} \cup L^{3} \cup \cdots \\&=\{a, 42,
\text { aa, } a 42,42 a, 4242, \text { aaa, } a a 42, a 42 a, \text { a4242 }, 42 a a, \ldots\}\end{aligned}
L + = n ≥ 1 ⋃ L n = L 1 ∪ L 2 ∪ L 3 ∪ ⋯ = { a , 42 , aa, a 42 , 42 a , 4242 , aaa, aa 42 , a 42 a , a4242 , 42 aa , … }
L ∗ = ⋃ n ≥ 0 L n = L 0 ∪ L 1 ∪ L 2 ∪ L 3 ∪ ⋯ = { ε , a , 42 , aa, a 42 , 42 a , 4242 , a a a , a a 42 , a 42 a , a 4242 , 42 a a , … }
\begin{aligned}L^{*} &=\bigcup_{n \geq 0} L^{n}=L^{0} \cup L^{1} \cup L^{2} \cup L^{3} \cup \cdots
\\&=\{\varepsilon, a, 42, \text { aa, } a 42,42 \mathrm{a}, 4242, \mathrm{aaa}, \mathrm{aa} 42,
\mathrm{a} 42 \mathrm{a}, \mathrm{a} 4242,42 \mathrm{aa}, \ldots\}\end{aligned}
L ∗ = n ≥ 0 ⋃ L n = L 0 ∪ L 1 ∪ L 2 ∪ L 3 ∪ ⋯ = { ε , a , 42 , aa, a 42 , 42 a , 4242 , aaa , aa 42 , a 42 a , a 4242 , 42 aa , … }
d) ( L ⋅ L ) ∗ = L ∗ ⋅ L ∗ (L \cdot L)^{*}=L^{*} \cdot L^{*} ( L ⋅ L ) ∗ = L ∗ ⋅ L ∗
Wir formen diese Gleichungen um:
( L ⋅ L ) ∗ = ( L 2 ) ∗ (L \cdot L)^{*}= (L^2)^* ( L ⋅ L ) ∗ = ( L 2 ) ∗
L ∗ ⋅ L ∗ = ( L ∗ ) 2 L^{*} \cdot L^{*} = (L^*)^2 L ∗ ⋅ L ∗ = ( L ∗ ) 2
Wir wissen weiters, dass:
L ∗ = ⋃ n ≥ 0 L n L^{*}=\bigcup_{n \geq 0} L^{n} L ∗ = ⋃ n ≥ 0 L n
Daraus folgt:
( L 2 ) ∗ = ⋃ n ≥ 0 ( L 2 ) n = ⋃ n ≥ 0 L ( 2 ⋅ n ) = L 0 ∪ L 2 ∪ L 4 ∪ L 6 ∪ ⋯
\textcolor{pink}{(L^2)^*} = \bigcup_{n \geq 0} (L^2)^{n} =\bigcup_{n \geq 0} L^{\textcolor{pink}{(2\cdot
n)}} = L^{0} \cup L^{2} \cup L^{4} \cup L^{6} \cup \cdots
( L 2 ) ∗ = ⋃ n ≥ 0 ( L 2 ) n = ⋃ n ≥ 0 L ( 2 ⋅ n ) = L 0 ∪ L 2 ∪ L 4 ∪ L 6 ∪ ⋯
( L ∗ ) 2 = ( ⋃ n ≥ 0 L n ) ⋅ ( ⋃ n ≥ 0 L n ) = = ( L 0 ∪ L 1 ∪ L 2 ∪ L 3 ∪ ⋯ ) ⋅ ( L 0 ∪ L 1 ∪ L 2 ∪ L 3 ∪ ⋯ ) = = ( ( L 0 ⋅ L 0 ) ∪ ( L 0 ⋅ L 1 ) ∪ ( L 0 ⋅ L 2 ) ∪ ( L 0 ⋅ L 3 ) ∪ ⋯ ∪ ( L 1 ⋅ L 0 ) ∪ ( L 1 ⋅ L 1 ) ∪ ( L 1 ⋅ L 2 ) ∪ ( L 1 ⋅ L 3 ) ∪ … ) = = ( L 0 ⋅ ( ⋃ n ≥ 0 L n ) ) ∪ ( L 1 ⋅ ( ⋃ n ≥ 0 L n ) ) ∪ ( L 2 ⋅ ( ⋃ n ≥ 0 L n ) ) ∪ ⋯ = L ∗
\textcolor{pink}{(L^*)^2} = \bigg( \bigcup_{n \geq 0} L^{n}\bigg)\cdot \bigg(\bigcup_{n \geq 0} L^{n} \bigg)
= \\ = \bigg(L^{0} \cup L^{1} \cup L^{2} \cup L^{3} \cup \cdots\bigg) \cdot \bigg( L^{0} \cup L^{1} \cup
L^{2} \cup L^{3} \cup \cdots\bigg) = \\= \big((L^{0} \cdot L^{0}) \cup (L^{0} \cdot L^{1}) \cup (L^{0} \cdot
L^{2}) \cup (L^{0} \cdot L^{3}) \cup \dots \cup (L^{1} \cdot L^{0}) \cup (L^{1} \cdot L^{1}) \cup (L^{1}
\cdot L^{2}) \cup (L^{1} \cdot L^{3}) \cup \dots \big) =\\ = \big( L^0 \cdot ( \bigcup_{n \geq 0} L^{n})
\big) \cup \big( L^1 \cdot ( \bigcup_{n \geq 0} L^{n}) \big) \cup \big( L^2 \cdot ( \bigcup_{n \geq 0}
L^{n}) \big) \cup \dots = \textcolor{pink}{L^*}
( L ∗ ) 2 = ( ⋃ n ≥ 0 L n ) ⋅ ( ⋃ n ≥ 0 L n ) = = ( L 0 ∪ L 1 ∪ L 2 ∪ L 3 ∪ ⋯ ) ⋅ ( L 0 ∪ L 1 ∪ L 2 ∪ L 3 ∪ ⋯ ) = = ( ( L 0 ⋅ L 0 ) ∪ ( L 0 ⋅ L 1 ) ∪ ( L 0 ⋅ L 2 ) ∪ ( L 0 ⋅ L 3 ) ∪ ⋯ ∪ ( L 1 ⋅ L 0 ) ∪ ( L 1 ⋅ L 1 ) ∪ ( L 1 ⋅ L 2 ) ∪ ( L 1 ⋅ L 3 ) ∪ … ) = = ( L 0 ⋅ ( ⋃ n ≥ 0 L n ) ) ∪ ( L 1 ⋅ ( ⋃ n ≥ 0 L n ) ) ∪ ( L 2 ⋅ ( ⋃ n ≥ 0 L n ) ) ∪ ⋯ = L ∗
Daraus wird offensichtlich:
( L 2 ) ∗ ⊂ ( L ∗ ) 2 = L ∗ (L^2)^*\sub(L^*)^2 = \textcolor{pink}{L^*} ( L 2 ) ∗ ⊂ ( L ∗ ) 2 = L ∗
Denn
L ∗ L^* L ∗
Gegenbeispiel:
L = { a , 42 } L=\{\mathrm{a}, 42\} L = { a , 42 }
L 2 = L ⋅ L ⋅ { ε } = L ⋅ L = { a a , a 42 , 42 a , 4242 }
L^{2} = L \cdot L \cdot \{\varepsilon\} = L \cdot L = \{aa, a42,42 a, 4242\}
L 2 = L ⋅ L ⋅ { ε } = L ⋅ L = { aa , a 42 , 42 a , 4242 }
( L ∗ ) 2 = L ∗ = ⋃ n ≥ 0 L n = L 0 ∪ L 1 ∪ L 2 ∪ L 3 ∪ ⋯ = { ε , a , 42 , aa, a 42 , 42 a , 4242 , a a a , a a 42 , a 42 a , a 4242 , 42 a a , … }
\begin{aligned}(L^*)^2 = \textcolor{pink}{L^*}&=\bigcup_{n \geq 0} L^{n}=L^{0} \cup L^{1} \cup L^{2}
\cup L^{3} \cup \cdots \\&=\{\varepsilon, a, 42, \text { aa, } a 42,42 \mathrm{a}, 4242, \mathrm{aaa},
\mathrm{aa} 42, \mathrm{a} 42 \mathrm{a}, \mathrm{a} 4242,42 \mathrm{aa}, \ldots\}\end{aligned}
( L ∗ ) 2 = L ∗ = n ≥ 0 ⋃ L n = L 0 ∪ L 1 ∪ L 2 ∪ L 3 ∪ ⋯ = { ε , a , 42 , aa, a 42 , 42 a , 4242 , aaa , aa 42 , a 42 a , a 4242 , 42 aa , … }
( L ⋅ L ) ∗ = ( L 2 ) ∗ = ⋃ n ≥ 0 L ( 2 ⋅ n ) = L 0 ∪ L 1 ∪ L 2 ∪ L 4 ∪ L 6 ∪ L 8 ∪ ⋯
(L \cdot L)^{*}= (L^2)^* = \bigcup_{n \geq 0} L^{\textcolor{pink}{(2\cdot n)}}= L^{0} \cup L^{1} \cup L^{2}
\cup L^{4} \cup L^{6} \cup L^{8} \cup \cdots
( L ⋅ L ) ∗ = ( L 2 ) ∗ = ⋃ n ≥ 0 L ( 2 ⋅ n ) = L 0 ∪ L 1 ∪ L 2 ∪ L 4 ∪ L 6 ∪ L 8 ∪ ⋯
Aufgabe 4 Gegeben:
A 1 = ⟨ Q 1 , Σ , δ 1 , i 1 , F 1 ⟩
\mathcal{A}_{1}=\left\langle Q_{1}, \Sigma, \delta_{1}, i_{1}, F_{1}\right\rangle
A 1 = ⟨ Q 1 , Σ , δ 1 , i 1 , F 1 ⟩
A 2 = ⟨ Q 2 , Σ , δ 2 , i 2 , F 2 ⟩
\mathcal{A}_{2}=\left\langle Q_{2}, \Sigma, \delta_{2}, i_{2}, F_{2}\right\rangle
A 2 = ⟨ Q 2 , Σ , δ 2 , i 2 , F 2 ⟩
Suche: Automat
A \mathcal A A
L ( A ) = L ( A 1 ) ∩ L ( A 2 )
\mathcal{L}(\mathcal{A})=\mathcal{L}\left(\mathcal{A}_{1}\right) \cap
\mathcal{L}\left(\mathcal{A}_{2}\right)
L ( A ) = L ( A 1 ) ∩ L ( A 2 )
Die Zustände und die jeweiligen Bezeichnungen dafür sind irrelevant, wichtig ist dass man für die gleichen Wörter zum Endzustand kommt.
Wir führen eine neue Notation ein:
Q 1 Q 2 Q_1Q_2 Q 1 Q 2 A \mathcal A A A 1 \mathcal A_1 A 1 Q 1 Q_1 Q 1 A 2 \mathcal A_2 A 2 Q 2 Q_2 Q 2
Definition:
A = ⟨ Q , Σ , δ , q 0 , F ⟩
\mathcal{A}=\left\langle Q, \Sigma, \delta, q_{0}, F\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩
Angenommen
Q 1 = { q 1 , 0 , q 1 , 1 , q 1 , 2 , … , q 1 , n 1 } Q 2 = { q 2 , 0 , q 2 , 1 , q 2 , 2 , … , q 2 , n 2 }
Q_1 = \{q_{1,0},q_{1,1},q_{1,2},\dots,q_{1,n_1}\} \quad Q_2 = \{q_{2,0},q_{2,1},q_{2,2},\dots,q_{2,n_2}\}
Q 1 = { q 1 , 0 , q 1 , 1 , q 1 , 2 , … , q 1 , n 1 } Q 2 = { q 2 , 0 , q 2 , 1 , q 2 , 2 , … , q 2 , n 2 }
Q = { q 1 , j q 1 , k ∣ j = [ 0 ; n 1 ] , k = [ 0 ; n 2 ] } ∪ trap
Q = \{q_{1, j}q_{1,k} \mid j = [0;n_1], ~~k = [0;n_2] \} \cup \text{trap}
Q = { q 1 , j q 1 , k ∣ j = [ 0 ; n 1 ] , k = [ 0 ; n 2 ]} ∪ trap
(jede mögliche Kombination an Zuständen soll möglich sein + Falle)
q 0 = i 1 i 2 ∈ Q q_{0} = i_1i_2 \in Q q 0 = i 1 i 2 ∈ Q
Angenommen
F 1 = { f 1 , 0 , f 1 , 1 , f 1 , 2 , … , f 1 , n 1 } F 2 = { f 2 , 0 , f 2 , 1 , f 2 , 2 , … , f 2 , n 2 }
F_1 = \{f_{1,0},f_{1,1},f_{1,2},\dots,f_{1,n_1}\} \quad F_2 = \{f_{2,0},f_{2,1},f_{2,2},\dots,f_{2,n_2}\}
F 1 = { f 1 , 0 , f 1 , 1 , f 1 , 2 , … , f 1 , n 1 } F 2 = { f 2 , 0 , f 2 , 1 , f 2 , 2 , … , f 2 , n 2 }
Dann
F = { f 0 , j f 1 , k ∣ j = [ 0 ; n 1 ] , k = [ 0 ; n 2 ] } F = \{f_{0,j}f_{1,k} \mid j = [0;n_1], ~~k = [0;n_2]\} F = { f 0 , j f 1 , k ∣ j = [ 0 ; n 1 ] , k = [ 0 ; n 2 ]}
Erweiterte Übergangsfunktion (auch für Leerwort)
Idee: Wenn es vom Eingabezustand und Eingabebuchstaben in beiden Automaten
A 1 \mathcal A_1 A 1 A 2 \mathcal A_2 A 2
δ ∗ : Q × Σ ∗ ↦ Q \delta^*: Q \times \Sigma^* \mapsto Q δ ∗ : Q × Σ ∗ ↦ Q
∀ q 1 ∈ Q 1 , q 2 ∈ Q 2 , s ∈ Σ , w ∈ Σ ∗ :
\forall q_1 \in Q_1, q_2 \in Q_2, s \in \Sigma, w \in \Sigma^{*}:
∀ q 1 ∈ Q 1 , q 2 ∈ Q 2 , s ∈ Σ , w ∈ Σ ∗ :
δ ∗ ( q 1 q 2 , s ) = { ( δ ∗ ( s ) ) ⋅ ( δ ∗ ( s ) ) if ∃ w : ( δ 1 ∗ ( q 1 , s w ) ∈ F ) ∧ ( δ 2 ∗ ( q 2 , s w ) ∈ F ) trap , otherwise
\delta^*(q_1q_2,s) = \begin{cases} (\delta^*(s))\cdot(\delta^*(s))& \text{if } \exists w:
\big(\delta^{*}_1\left(q_{1}, sw\right) \in F \big) \wedge \big(\delta^{*}_2\left(q_{2}, sw\right) \in F
\big) \\ \text{trap}, & \text{otherwise} \end{cases}
δ ∗ ( q 1 q 2 , s ) = { ( δ ∗ ( s )) ⋅ ( δ ∗ ( s )) trap , if ∃ w : ( δ 1 ∗ ( q 1 , s w ) ∈ F ) ∧ ( δ 2 ∗ ( q 2 , s w ) ∈ F ) otherwise
Akzeptierte / Generierte Sprache
Nur Wörter die von
initial state
zu einem
final state
führen.
L ( A ) = { w ∈ Σ ∗ ∣ δ ∗ ( q 0 , w ) ∈ F } = L ( A 1 ) ∩ L ( A 2 )
\mathcal{L}(\mathcal{A})=\left\{w \in \Sigma^{*} \mid \delta^{*}\left(q_{0}, w\right) \in F\right\} =
\mathcal{L}\left(\mathcal{A}_{1}\right) \cap \mathcal{L}\left(\mathcal{A}_{2}\right)
L ( A ) = { w ∈ Σ ∗ ∣ δ ∗ ( q 0 , w ) ∈ F } = L ( A 1 ) ∩ L ( A 2 )
Aufgabe 5
Ziel: Automat
→ \rarr → → \rarr →
Regeln
keine Kanten zum Anfangszustand nur ein Endzustand (ohne Kanten weg) der kein Eingangszustand ist Übergänge beschriftet mit regulären Ausdrücken
Problem: Unser Anfangszustand ist ein Endzustand und wir haben mehrere Endzustände.
Geeignetes Automat
Algorithmus
Für jeden Zustand
q ∈ Q − { i , f } q \in Q-\{i, f\} q ∈ Q − { i , f }
Füge zwischen allen Nachbarn
p , p ′ p, p' p , p ′ q q q
Entferne
q q q q q q
Resultat
Zustand
0 0 0
Zustand
1 1 1
Zustand
2 2 2
Aufgabe 6 a) Algebraische Notation g r u p p e = I + I I gruppe = I + II g r u pp e = I + II
k a t e g o r i e = ( 1 + 2 + 3 ) ( ε + ( G + D ) ) kategorie= (1 +2+3 )(\varepsilon+(G+D)) ka t e g or i e = ( 1 + 2 + 3 ) ( ε + ( G + D ))
e x = ( ε + E x ) ex= (\varepsilon+Ex) e x = ( ε + E x )
g r o ß b u c h s t a b e = ( A + B + C + ⋯ + Z ) großbuchstabe = (A+B+C+\dots+Z) g ro ß b u c h s t ab e = ( A + B + C + ⋯ + Z )
z u ¨ n d a r t = ( a + b + c + ⋯ + z ) ( ( a + b + c + ⋯ + z ) + g r o ß b u c h s t a b e + ( 0 + 1 + 2 + 3 + ⋯ + 9 ) ) ∗
zündart = (a+b+c+\dots+z)((a+b+c+\dots+z)+großbuchstabe+(0+1+2+3+\dots+9))^*
z u ¨ n d a r t = ( a + b + c + ⋯ + z ) (( a + b + c + ⋯ + z ) + g ro ß b u c h s t ab e + ( 0 + 1 + 2 + 3 + ⋯ + 9 ) ) ∗
e x g r = I I g r o ß b u c h s t a b e exgr=IIgroßbuchstabe e xg r = II g ro ß b u c h s t ab e
k l a s s e = T ( 1 + 2 + ⋯ + 6 ) klasse = T(1+2+\dots+6) k l a sse = T ( 1 + 2 + ⋯ + 6 )
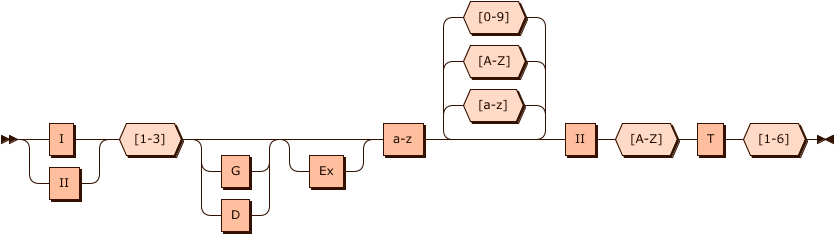
s c h i l d = g r u p p e ␣ k a t e g o r i e ␣ e x ␣ z u ¨ n d a r t ␣ e x g r ␣ k l a s s e schild= gruppe␣kategorie␣ex␣zündart␣exgr␣klasse sc hi l d = g r u pp e ␣ ka t e g or i e ␣ e x ␣ z u ¨ n d a r t ␣ e xg r ␣ k l a sse
b) POSIX Notation schild = ˆ (I|II)␣[1-3](G|D)?␣(Ex)?␣(a-z)[a-zA-Z0-9]*␣II[A-Z]␣T[1-6]$
\texttt{schild = \^{}(I|II)␣[1-3](G|D)?␣(Ex)?␣(a-z)[a-zA-Z0-9]*␣II[A-Z]␣T[1-6]\$}
schild = ˆ (I|II)␣[1-3](G|D)?␣(Ex)?␣(a-z)[a-zA-Z0-9]*␣II[A-Z]␣T[1-6]$
c) Syntaxdiagramm schild:
Aufgabe 7 G = ⟨ N , T , P , A ⟩ G=\langle N, T, P, A\rangle G = ⟨ N , T , P , A ⟩
N = { A , B , C , D } T = { h , s c h , s c h u , u h u , u u } P = { A → sch uhu A ∣ uhu ∣ B , B → h uhu C C → uhu D D → schu D ∣ u u ∣ A }
\begin{aligned}N=&\{A, B, C, D\} \\T=&\{\mathrm{h}, \mathrm{sch}, \mathrm{schu}, \mathrm{uhu},
\mathrm{uu}\} \\P=&\{A \rightarrow \operatorname{sch} \text { uhu } A \mid \text { uhu } \mid B,\\& B
\rightarrow \text { h uhu } C \\& C \rightarrow \text { uhu } D \\&D \rightarrow \operatorname{schu}
D|\mathrm{uu}| A\}\end{aligned}
N = T = P = { A , B , C , D } { h , sch , schu , uhu , uu } { A → sch uhu A ∣ uhu ∣ B , B → h uhu C C → uhu D D → schu D ∣ uu ∣ A }
Von Grammatik G G G generierte Sprache
L ( G ) = { w ∈ T ∗ ∣ S ⇒ ∗ w }
\mathcal{L}(G)=\left\{w \in T^{*} \mid S \stackrel{*}{\Rightarrow} w\right\}
L ( G ) = { w ∈ T ∗ ∣ S ⇒ ∗ w }
Alle Wörter aus Terminal-Verknüpfungen bei denen ein Startsymbol nach Ableitung zu einem gültigen Wort führt.
Quasi Menge aller mit der Grammatik ableit-baren Wörter.
In diesem Fall muss jedes Wort entweder mit einem Terminal oder dem Nonterminal
A A A
a) h uhu uhu schu uu \texttt{h uhu uhu schu uu } h uhu uhu schu uu
A ⇒ P P ( B ) A \Rarr_P P(B) A ⇒ P P ( B )
⇒ P h uhu P ( C ) \Rarr_P \text{h uhu } P(C) ⇒ P h uhu P ( C )
⇒ P h uhu uhu P ( D ) \Rarr_P \text{h uhu uhu } P(D) ⇒ P h uhu uhu P ( D )
⇒ P h uhu uhu schu P ( D ) \Rarr_P \text{h uhu uhu schu } P(D) ⇒ P h uhu uhu schu P ( D )
⇒ P h uhu uhu schu uu \Rarr_P \text{h uhu uhu schu uu} ⇒ P h uhu uhu schu uu
b) sch uhu h uhu uhu schu schu sch uhu uhu \texttt{sch uhu h uhu uhu schu schu sch uhu uhu }
sch uhu h uhu uhu schu schu sch uhu uhu
A ⇒ P sch uhu P ( A ) A \Rarr_P \text{sch uhu } P(A) A ⇒ P sch uhu P ( A )
⇒ P sch uhu P ( B ) \Rarr_P \text{sch uhu } P(B) ⇒ P sch uhu P ( B )
⇒ P sch uhu h uhu P ( C ) \Rarr_P \text{sch uhu h uhu } P(C) ⇒ P sch uhu h uhu P ( C )
⇒ P sch uhu h uhu uhu P ( D ) \Rarr_P \text{sch uhu h uhu uhu } P(D) ⇒ P sch uhu h uhu uhu P ( D )
⇒ P sch uhu h uhu uhu schu P ( D ) \Rarr_P \text{sch uhu h uhu uhu schu } P(D) ⇒ P sch uhu h uhu uhu schu P ( D )
⇒ P sch uhu h uhu uhu schu schu P ( D ) \Rarr_P \text{sch uhu h uhu uhu schu schu } P(D) ⇒ P sch uhu h uhu uhu schu schu P ( D )
⇒ P sch uhu h uhu uhu schu schu P ( A ) \Rarr_P \text{sch uhu h uhu uhu schu schu } P(A) ⇒ P sch uhu h uhu uhu schu schu P ( A )
⇒ P sch uhu h uhu uhu schu schu sch uhu P ( A ) \Rarr_P \text{sch uhu h uhu uhu schu schu sch uhu } P(A) ⇒ P sch uhu h uhu uhu schu schu sch uhu P ( A )
⇒ P sch uhu h uhu uhu schu schu sch uhu uhu \Rarr_P \text{sch uhu h uhu uhu schu schu sch uhu uhu} ⇒ P sch uhu h uhu uhu schu schu sch uhu uhu
c) sch uhu sch uhu uhu uu \texttt{sch uhu sch uhu uhu uu} sch uhu sch uhu uhu uu
A ⇒ P sch uhu P ( A ) A \Rarr_P \text{sch uhu } P(A) A ⇒ P sch uhu P ( A )
⇒ P sch uhu sch uhu P ( A ) \Rarr_P \text{sch uhu sch uhu } P(A) ⇒ P sch uhu sch uhu P ( A )
⇒ P sch uhu sch uhu uhu \Rarr_P \text{sch uhu sch uhu uhu } ⇒ P sch uhu sch uhu uhu
Das erwünschte Wort lässt sich nicht erreichen weil wir zu früh ein Terminal erreichen.
sch \texttt{sch} sch A A A
Lösung:
sch uhu schu uhu uhu \texttt{sch uhu schu uhu uhu} sch uhu schu uhu uhu
d)
Das kürzeste Wort wäre ein Terminal mit der geringsten Buchstabenanzahl:
h \text{h} h
e)
Diese Sprache ist regulär / lässt sich mit einem endlichen Automaten beschreiben, weil sie nicht beliebig tief schachtelbar ist (wie bei
einem wohlgeformten Klammerausdruck).
P = { A → sch uhu A ∣ uhu ∣ B , B → h uhu C C → uhu D D → schu D ∣ u u ∣ A }
P=\{ \\A \rightarrow \operatorname{sch} \text { uhu } A \mid \text { uhu } \mid B, \\B \rightarrow \text { h uhu
} C \\C \rightarrow \text { uhu } D \\D \rightarrow \operatorname{schu} D~|~\mathrm{uu}~|~ A \\\}
P = { A → sch uhu A ∣ uhu ∣ B , B → h uhu C C → uhu D D → schu D ∣ uu ∣ A }
Ist äquivalent zur Grammatik:
P = { A → sch uhu A ∣ uhu ∣ h uhu uhu D , D → schu D ∣ u u ∣ A }
P=\{ \\A \rightarrow \operatorname{sch} \text { uhu } A \mid \text { uhu } \mid \text { h uhu} \text { uhu } D,
\\D \rightarrow \operatorname{schu } ~D~ | ~\mathrm{ uu }~| ~A \\\}
P = { A → sch uhu A ∣ uhu ∣ h uhu uhu D , D → schu D ∣ uu ∣ A }
Und lässt sich mit dem folgendem Automaten beschreiben:
Aufgabe 8 a) Als kontextfreie Grammatik (EBNF Notation) Vorteile der BNF:
Keine Angabe / Differenzierung zwischen Terminalen und Nonterminalen sowie Anfangsterminalen mehr notwendig weil es sich von der
Notation selbst ablesen lässt.
Man gibt nur noch die Produktionen an.
Vorteile der EBNF (verglichen zur BNF):
Leichtere Syntax ohne
(<, >, |, ::=)
indem zwischen Terminalen und Nonterminalen mit
""
differenziert wird.
Abkürzungen aus regulären Ausdrücken übernommen wie
(), [], {}
.
buchstabe = "A" | "B" | "C" | "D" | "E" | "F" | "G"
| "H" | "I" | "J" | "K" | "L" | "M" | "N"
| "O" | "P" | "Q" | "R" | "S" | "T" | "U"
| "V" | "W" | "X" | "Y" | "Z" | kleinbuchstabekleinbuchstabe = "a" | "b" | "c" | "d" | "e" | "f" | "g"
| "h" | "i" | j" | "k" | "l" | "m" | "n"
| "o" | "p" | q" | "r" | "s" | "t" | "u"
| "v" | "w" | x" | "y" | "z"ordner = buchstabe {buchstabe} "[" [liste] "]"liste = "," datei | "," ordner | listedatei = dateiname "." dateiendungdateiname = buchstabe [buchstabe] [buchstabe] [buchstabe]dateiendung = kleinbuchstabe kleinbuchstabe [kleinbuchstabe]
b) Als regulärer Ausdruck (algebraische Notation) k l e i n b u c h s t a b e = a + b + c + ⋯ + z kleinbuchstabe = a+b+c+\dots+z k l e inb u c h s t ab e = a + b + c + ⋯ + z
b u c h s t a b e = ( k l e i n b u c h s t a b e + ( A + B + C + ⋯ + Z ) ) buchstabe = (kleinbuchstabe+ (A+B+C+\dots+Z)) b u c h s t ab e = ( k l e inb u c h s t ab e + ( A + B + C + ⋯ + Z ))
o r d n e r = b u c h s t a b e ( b u c h s t a b e ) ∗ [ i n h a l t ] ordner = buchstabe(buchstabe)^*[inhalt] or d n er = b u c h s t ab e ( b u c h s t ab e ) ∗ [ inha lt ]
i n h a l t = ε + l i s t e inhalt = \varepsilon + liste inha lt = ε + l i s t e
l i s t e = ε + , d a t e i + , o r d n e r + l i s t e liste= \varepsilon+,datei+,ordner+liste l i s t e = ε + , d a t e i + , or d n er + l i s t e
d a t e i n a m e = b u c h s t a b e ( b u c h s t a b e + ε ) ( b u c h s t a b e + ε ) ( b u c h s t a b e + ε )
dateiname= buchstabe (buchstabe+\varepsilon) (buchstabe+\varepsilon) (buchstabe+\varepsilon)
d a t e inam e = b u c h s t ab e ( b u c h s t ab e + ε ) ( b u c h s t ab e + ε ) ( b u c h s t ab e + ε )
d a t e i e n d u n g = ( k l e i n b u c h s t a b e ) ( k l e i n b u c h s t a b e ) ( k l e i n b u c h s t a b e + ε )
dateiendung = (kleinbuchstabe)(kleinbuchstabe)(kleinbuchstabe+\varepsilon)
d a t e i e n d u n g = ( k l e inb u c h s t ab e ) ( k l e inb u c h s t ab e ) ( k l e inb u c h s t ab e + ε )
d a t e i = d a t e i n a m e . d a t e i e n d u n g datei = dateiname.dateiendung d a t e i = d a t e inam e . d a t e i e n d u n g
Aufgabe 9 a) Hakan kauft etwas. P = { Hakan / 1 , Kauft / 2 } \mathcal{P}=\{\text{Hakan } /1,\text { Kauft } / 2\} P = { Hakan /1 , Kauft /2 }
Mögliche Modellierungen:
∃ x ( Hakan ( x ) ⊃ ∃ y ( Kauft ( x , y ) ) )
\exists x~(\text{Hakan}(x) \supset \exists y~(\text{Kauft}(x,y)))
∃ x ( Hakan ( x ) ⊃ ∃ y ( Kauft ( x , y )))
∃ x , y ( Hakan ( x ) ∧ ( Kauft ( x , y ) ) \exists x,y ~(\text{Hakan}(x) \wedge(\text{Kauft}(x,y)) ∃ x , y ( Hakan ( x ) ∧ ( Kauft ( x , y ))
b) Hakan kauft eine DVD. P = { Hakan / 1 , Kauft / 2 , CD / 1 }
\mathcal{P}=\{\text{Hakan } /1,\text { Kauft } / 2, \text { CD } / 1\}
P = { Hakan /1 , Kauft /2 , CD /1 }
Mögliche Modellierungen:
∃ x ( Hakan ( x ) ⊃ ( ∃ y ( CD ( y ) ∧ Kauft ( x , y ) ) ) )
\exists x~(\text{Hakan}(x) \supset (\exists y~(\text{CD}(y) \wedge \text{Kauft}(x,y))))
∃ x ( Hakan ( x ) ⊃ ( ∃ y ( CD ( y ) ∧ Kauft ( x , y ))))
∃ x , y ( Hakan ( x ) ∧ CD ( y ) ∧ Kauft ( x , y ) )
\exists x,y ~(\text{Hakan}(x) \wedge\text{CD}(y) \wedge \text{Kauft}(x,y))
∃ x , y ( Hakan ( x ) ∧ CD ( y ) ∧ Kauft ( x , y ))
c) Anna kauft alles das, was Hakan kauft. P = { Hakan / 1 , Kauft / 2 , Anna / 1 }
\mathcal{P}=\{\text{Hakan } /1,\text { Kauft } / 2, \text { Anna } / 1\}
P = { Hakan /1 , Kauft /2 , Anna /1 }
Mögliche Modellierung:
∃ x , y ( Hakan ( x ) ∧ Anna ( y ) ⊃ ∀ z ( Kauft ( x , z ) ⊃ Kauft ( y , z ) ) )
\exists x,y ~(\text{Hakan}(x) \wedge \text{Anna}(y) \supset \forall z ~(\text{Kauft}(x,z) \supset
\text{Kauft}(y,z)))
∃ x , y ( Hakan ( x ) ∧ Anna ( y ) ⊃ ∀ z ( Kauft ( x , z ) ⊃ Kauft ( y , z )))
d) Jeder kauft etwas. P = { Mensch / 1 , Kauft / 2 } \mathcal{P}=\{\text{Mensch } /1,\text { Kauft } / 2\} P = { Mensch /1 , Kauft /2 }
Mögliche Modellierung:
∀ x ∃ y ( Mensch ( x ) ⊃ Kauft ( x , y ) )
\forall x \exist y ~ (\text{Mensch}(x) \supset \text{Kauft}(x,y))
∀ x ∃ y ( Mensch ( x ) ⊃ Kauft ( x , y ))
e) Jemand kauft alles. P = { Mensch / 1 , Kauft / 2 } \mathcal{P}=\{\text{Mensch } /1,\text { Kauft } / 2\} P = { Mensch /1 , Kauft /2 }
Mögliche Modellierung:
∃ x ∀ y ( Mensch ( x ) ⊃ Kauft ( x , y ) )
\exists x \forall y ~ (\text{Mensch}(x) \supset \text{Kauft}(x,y))
∃ x ∀ y ( Mensch ( x ) ⊃ Kauft ( x , y ))
Aufgabe 10 Universum, Prädikate, Funktionen U = {
Obi-Wan, Yoda, Luke, Anakin, DarthVader, DarthBane, DarthMaul,
DarthTyrannus, DarthSidious, Yaddle}
\mathcal{U}=\{\text { Obi-Wan, Yoda, Luke, Anakin, DarthVader, DarthBane, DarthMaul, }\\\text { DarthTyrannus,
DarthSidious, Yaddle\} }
U = {
Obi-Wan, Yoda, Luke, Anakin, DarthVader, DarthBane, DarthMaul,
DarthTyrannus, DarthSidious, Yaddle}
P = { B e k a ¨ m p f t / 2 , J e d i / 1 , S i t h / 1 , D u n k e l / 1 } \mathcal{P}=\{Bekämpft/2,~Jedi/1,~Sith/1,~Dunkel/1 \} P = { B e k a ¨ m p f t /2 , J e d i /1 , S i t h /1 , D u nk e l /1 }
F = { yoda / 0 , luke / 0 , d a r t h v a d e r / 0 } \mathcal{F}=\{\text {yoda}/ 0, ~\text{luke}/0, ~darthvader/0\} F = { yoda /0 , luke /0 , d a r t h v a d er /0 }
a) Es gibt dunkle Sith, die alle Jedi-Ritter bekämpfen.
Mögliche Modellierungen:
∃ x ( ( D u n k e l ( x ) ∧ S i t h ( x ) ) ⊃ ∀ y ( J e d i ( y ) ∧ B e k a ¨ m p f t ( x , y ) ) )
\exists x~ ((Dunkel(x) \wedge Sith(x)) \supset \forall y ~(Jedi(y)\wedge Bekämpft(x,y)))
∃ x (( D u nk e l ( x ) ∧ S i t h ( x )) ⊃ ∀ y ( J e d i ( y ) ∧ B e k a ¨ m p f t ( x , y )))
∃ x ∀ y ( D u n k e l ( x ) ∧ S i t h ( x ) ∧ ( J e d i ( y ) ∧ B e k a ¨ m p f t ( x , y ) )
\exists x \forall y~ (Dunkel(x) \wedge Sith(x) \wedge (Jedi(y)\wedge Bekämpft(x,y))
∃ x ∀ y ( D u nk e l ( x ) ∧ S i t h ( x ) ∧ ( J e d i ( y ) ∧ B e k a ¨ m p f t ( x , y ))
b) Kein Jedi-Ritter bekämft alle Sith.
Mögliche Modellierung:
¬ ( ∃ x ∀ y ( J e d i ( x ) ∧ S i t h ( y ) ∧ B e k a ¨ m p f t ( x , y ) ) )
\neg (\exists x \forall y ~(Jedi(x) \wedge Sith(y) \wedge Bekämpft(x,y)))
¬ ( ∃ x ∀ y ( J e d i ( x ) ∧ S i t h ( y ) ∧ B e k a ¨ m p f t ( x , y )))
Interpretationen I ( J e d i ) = { Obi-Wan, Yoda, Luke, DarthVader, Yaddle }
I(J e d i)=\{\text { Obi-Wan, Yoda, Luke, DarthVader, Yaddle }\}
I ( J e d i ) = { Obi-Wan, Yoda, Luke, DarthVader, Yaddle }
I ( S i t h ) = { DarthVader, DarthBane, DarthMaul, DarthTyrannus}
I( Sith )=\{\text { DarthVader, DarthBane, DarthMaul, DarthTyrannus\} }
I ( S i t h ) = { DarthVader, DarthBane, DarthMaul, DarthTyrannus}
I ( D u n k e l ) = { DarthBane, DarthVader, Anakin } I(Dunkel)=\{\text { DarthBane, DarthVader, Anakin }\} I ( D u nk e l ) = { DarthBane, DarthVader, Anakin }
I ( B e k a ¨ m p f t ) = { (
Obi-Wan, DarthTyrannus), (Obi-Wan, DarthBane), (Obi-Wan, DarthMaul),
(Yoda, DarthMaul), (Yoda, DarthTyrannus), (DarthVader, Luke), (DarthVader, DarthVader),
(Anakin, Obi-Wan), (Anakin, Luke), (Anakin, DarthVader),
(DarthBane, Obi-Wan), (DarthBane, Luke), (DarthBane, Yoda),
(DarthSidious, Yaddle)}
\begin{aligned}I(Bekämpft)=~&\{(\text { Obi-Wan, DarthTyrannus), (Obi-Wan, DarthBane), (Obi-Wan, DarthMaul),
}\\& \text { (Yoda, DarthMaul), (Yoda, DarthTyrannus), } \\&\text { (DarthVader, Luke), (DarthVader,
DarthVader), } \\& \text { (Anakin, Obi-Wan), (Anakin, Luke), (Anakin, DarthVader), } \\&\text {
(DarthBane, Obi-Wan), (DarthBane, Luke), (DarthBane, Yoda), } \\& \text { (DarthSidious, Yaddle)\} }
\end{aligned}
I ( B e k a ¨ m p f t ) = {(
Obi-Wan, DarthTyrannus), (Obi-Wan, DarthBane), (Obi-Wan, DarthMaul),
(Yoda, DarthMaul), (Yoda, DarthTyrannus),
(DarthVader, Luke), (DarthVader, DarthVader),
(Anakin, Obi-Wan), (Anakin, Luke), (Anakin, DarthVader),
(DarthBane, Obi-Wan), (DarthBane, Luke), (DarthBane, Yoda),
(DarthSidious, Yaddle)} I ( l u k e ) = Luke I(luke )=\text { Luke } I ( l u k e ) = Luke
I ( d a r t h v a d e r ) = DarthVader I({ darthvader })=\text { DarthVader } I ( d a r t h v a d er ) = DarthVader
c) ∃ x ( Dunkel ( x ) ∧ Sith ( x ) ∧ ( Bek a ¨ mpft ( x , luke ) ≢ Bek a ¨ mpft ( x , darthvader ) ) )
\exists x(\text {Dunkel }(x) \wedge \operatorname{Sith}(x) \wedge(\text { Bekämpft }(x, \text { luke }) \not
\equiv \text { Bekämpft }(x, \text { darthvader })))
∃ x ( Dunkel ( x ) ∧ Sith ( x ) ∧ ( Bek a ¨ mpft ( x , luke ) ≡ Bek a ¨ mpft ( x , darthvader )))
Es gibt mindestens einen dunklen Sith der entweder Luke oder Darthvader bekämpft aber nicht beide gemeinsam.
Überprüfung dieser Aussage
Die dunklen Sith sind {DarthBane, DarthVader}
DarthBane bekämpft: {Obi-Wan, Luke, Yoda} → mit der Interpretation
x = DarthBane x = \text{DarthBane} x = DarthBane
DarthVader bekämpft: {Luke, DarthVader} → mit der Interpretation
x = DarthVader x = \text{DarthVader} x = DarthVader
Durch den Existenzquantor wird die Erfüllbarkeit der Formel mit einer beliebigen Belegung für
x x x
Für alle
I , σ I, \sigma I , σ val I , σ ( F ) = 1 \textsf{val}_{I,\sigma}(F) = 1 val I , σ ( F ) = 1
d) ∀ x ∃ y ( Jedi ( x ) ∧ Sith ( y ) ∧ B e k a ¨ m p f t ( x , y ) )
\forall x \exists y(\operatorname{Jedi} (x) \wedge \operatorname{Sith}(y) \wedge \operatorname{Bekämpft}(x, y))
∀ x ∃ y ( Jedi ( x ) ∧ Sith ( y ) ∧ Bek a ¨ mpft ( x , y ))
Alle Jedis bekämpfen mindestens einen Sith.
Überprüfung dieser Aussage
Alle Jedis sind: {Obi-Wan, Yoda, Luke, DarthVader, Yaddle} Alle Sith sind: {DarthVader, DarthBane, DarthMaul, DarthTyrannus}
Dadurch ist diese Formel
widerlegbar
denn für mindestens eine
I , σ I, \sigma I , σ val I , σ ( F ) = 0 \textsf{val}_{I,\sigma}(F) = 0 val I , σ ( F ) = 0
e) ∀ x ( Jedi ( x ) ⊃ ∃ y ( Sith ( y ) ∧ B e k a ¨ m p f t ( y , x ) ) )
\forall x(\operatorname{Jedi}(x) \supset \exists y(\operatorname{Sith}(y) \wedge \operatorname{Bekämpft}(y, x)))
∀ x ( Jedi ( x ) ⊃ ∃ y ( Sith ( y ) ∧ Bek a ¨ mpft ( y , x )))
Alle Jedis werden von mindestens einem Sith bekämpft.
Überprüfung dieser Aussage
Alle Jedis sind: {Obi-Wan, Yoda, Luke, DarthVader, Yaddle} Alle Sith sind: {DarthVader, DarthBane, DarthMaul, DarthTyrannus} Yaddle wird nur von DarthSidious bekämpft, welcher kein Sith ist
Dadurch ist diese Formel
widerlegbar
denn für mindestens eine
I , σ I, \sigma I , σ val I , σ ( F ) = 0 \textsf{val}_{I,\sigma}(F) = 0 val I , σ ( F ) = 0
Aufgabe 11 Petri-Netz → endlicher Automat
Bezeichnungen der Transitionen
{ t 1 , t 2 , t 3 , t 4 } \{t_1, t_2, t_3, t_4\} { t 1 , t 2 , t 3 , t 4 } Σ \Sigma Σ
Belegung einer Stelle mit einem Token = Zustand
Q Q Q
A = ⟨ Q , Σ , δ , q 0 , F ⟩
\mathcal{A}=\left\langle Q, \Sigma, \delta, q_{0}, F\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩ finite automaton
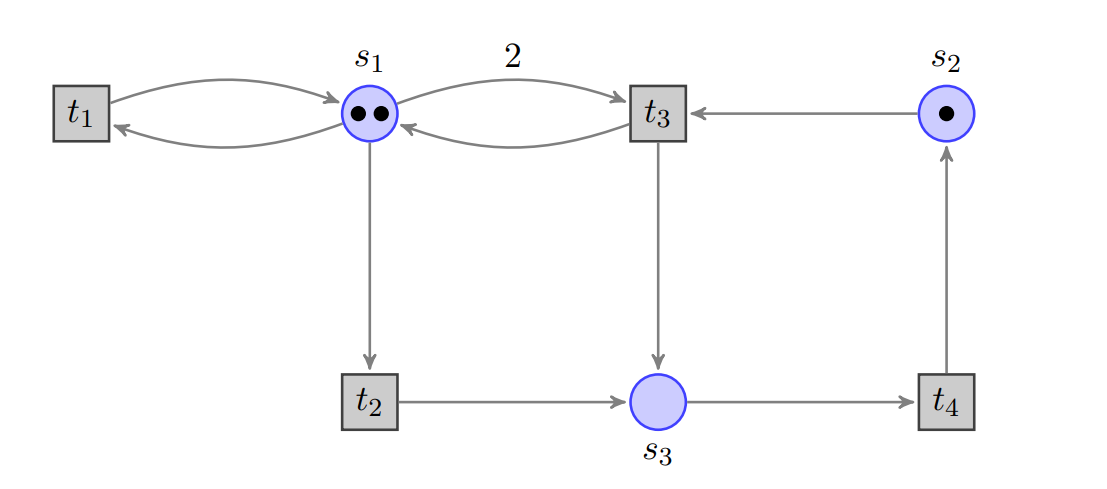
Q = { 210 , 101 , 111 , 110 , 002 , 010 , 012 , 011 , 021 , 020 , 030 } Q = \{210,101,111,110,002,010,012,011,021,020,030\} Q = { 210 , 101 , 111 , 110 , 002 , 010 , 012 , 011 , 021 , 020 , 030 } all possible states (finite)
Die Stelle der dreistelligen Ziffer
☐☐☐ ☐☐☐ ☐☐☐ s 1 s_1 s 1 s 3 s_3 s 3
∑ = { t 1 , t 2 , t 3 , t 4 } \sum = \{t_1, t_2, t_3, t_4\} ∑ = { t 1 , t 2 , t 3 , t 4 } input alphabet
δ : Q × Σ ↦ Q \delta: Q \times \Sigma \mapsto Q δ : Q × Σ ↦ Q transition function
Diese lässt sich aus unterer Abbildung herleiten.
q 0 = 210 q_{0} = 210 q 0 = 210 initial state
F = { 020 , 030 } F = \{020,030\} F = { 020 , 030 } final states
Aufgabe 12 a) Brücke für Fahrzeuge
2 Spuren, für 2 Richtungen - in beiden Richtungen befahrbar
Fahrzeugpositionen:
{ v o r B r u ¨ c k e , a u f B r u ¨ c k e , n a c h B r u ¨ c k e } \{vorBrücke, aufBrücke, nachBrücke\} { v or B r u ¨ c k e , a u f B r u ¨ c k e , na c h B r u ¨ c k e }
Anfangszustand: Alle Fahrzeuge möchten Brücke überqueren
Eine Seite 4 Fahrzeuge
Andere Seite 2 Fahrzeuge
Brücke selbst leer
Wir haben insgesamt 6 Stellen:
{ v o r O b e n , a u f O b e n , n a c h O b e n , v o r U n t e n , a u f U n t e n , n a c h U n t e n }
\{\ vorOben,~aufOben,~nachOben,~vorUnten,~aufUnten,~nachUnten\}
{ v or O b e n , a u f O b e n , na c h O b e n , v or U n t e n , a u f U n t e n , na c h U n t e n }
Ein Fahrzeug kann vor, auf und nach der Brücke sein und je in der linken oder rechten Spur.
Zur Einfachheit habe ich meine Spuren statt Links / Rechts in meinem Modell oben / unten genannt.
b) Nur 3 Fahrzeuge gleichzeitig auf der Brücke erlaubt, unabhängig von Fahrtrichtung.
Das entspricht einem Buffer mit 3 Tokens.
c) d) Wenn eine Reperatur stattfindet:
Ampeln installiert, abwechselnd grün (wenn Brücke komplett leer) Fahrzeuge fahren nur wenn: Grün, max 3 Fahrzeuge auf Brücke
Hinweis: diesmal habe ich die Stellen der Fahrzeug-Spuren im Modell vertauscht damit das Modellieren einfacher ist.
Es kommt auch zu keinen Kollisionen, dadurch, dass die Buffer der einzelnen Seiten unabhängig voneinander sind und eine Seite komplett leer
sein muss bevor die Ampel schaltet.