Definition 📌
Definition, Automatenarten
Deterministische endliche Automaten DEA A = ⟨ Q , Σ , δ , q 0 , F ⟩
\mathcal{A}=\left\langle Q, \Sigma, \delta, q_{0}, F\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩
Q Q Q all possible states (finite)
∑ \sum ∑ input alphabet
(kein
ε \varepsilon ε
δ : Q × Σ ↦ Q \delta: Q \times \Sigma \mapsto Q δ : Q × Σ ↦ Q transition function
Totale Funktion: Funktion, die für jeden Wert aus Definitonsmenge ein Abbild hat. Deshalb deterministisch.
q 0 ∈ Q q_{0} \in Q q 0 ∈ Q initial state
F ⊆ Q F \subseteq Q F ⊆ Q final states
Erweiterte Übergangsfunktion (auch für Leerwort)
δ ∗ : Q × Σ ∗ ↦ Q \delta^{*}: Q \times \Sigma^{*} \mapsto Q δ ∗ : Q × Σ ∗ ↦ Q
∀ q ∈ Q , s ∈ Σ , w ∈ Σ ∗ : δ ∗ ( q , ε ) = q , δ ∗ ( q , s w ) = δ ∗ ( δ ( q , s ) , w )
\forall q \in Q, s \in \Sigma, w \in \Sigma^{*}: \quad \delta^{*}(q, \varepsilon)=q, \quad \delta^{*}(q, s
w)=\delta^{*}(\delta(q, s), w)
∀ q ∈ Q , s ∈ Σ , w ∈ Σ ∗ : δ ∗ ( q , ε ) = q , δ ∗ ( q , s w ) = δ ∗ ( δ ( q , s ) , w )
Akzeptierte / Generierte Sprache
Nur Wörter die von
initial state
zu einem
final state
führen.
L ( A ) = { w ∈ Σ ∗ ∣ δ ∗ ( q 0 , w ) ∈ F }
\mathcal{L}(\mathcal{A})=\left\{w \in \Sigma^{*} \mid \delta^{*}\left(q_{0}, w\right) \in F\right\}
L ( A ) = { w ∈ Σ ∗ ∣ δ ∗ ( q 0 , w ) ∈ F }
Falle / Fehlerzustand
Wird meistens nicht eingezeichnet aber existiert in Tabelle.
Alle Fehlverhalten → Falle, dann kein Weg heraus.
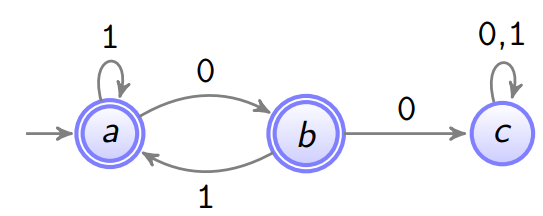
Beispiel:
00-freie Binärstrings c c c
Q = { a , b , c } Q=\{a, b, c\} Q = { a , b , c }
Σ = { 0 , 1 } \Sigma=\{0,1\} Σ = { 0 , 1 }
q 0 = a q_0 = a q 0 = a
F = { a , b } F=\{a, b\} F = { a , b }
δ : Q × Σ ↦ Q \delta: Q \times \Sigma \mapsto Q δ : Q × Σ ↦ Q
δ 0 1 a b a b c a c c c
\begin{array}{l|ll}\delta & 0 & 1 \\\hline a & b & a \\b & c & a \\c
& c & c\end{array}
δ
a b c 0 b c c 1 a a c
Beispielsweise:
101 ∈ L ( A ) 101 \in \mathcal{L}(\mathcal{A}) 101 ∈ L ( A )
Nichtdeterministische endliche Automaten NEA A = ⟨ Q , Σ , δ , q 0 , F ⟩
\mathcal{A}=\left\langle Q, \Sigma, \delta, q_{0}, F\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩
Alles gleich mit DEA nur
ε \varepsilon ε
δ ⊆ Q × ( Σ ∪ { ε } ) × Q
\delta \subseteq Q \times(\Sigma \cup\{\varepsilon\}) \times Q
δ ⊆ Q × ( Σ ∪ { ε }) × Q
δ : Q × ( Σ ∪ { ε } ) ↦ 2 Q \delta: Q \times(\Sigma \cup\{\varepsilon\}) \mapsto 2^{Q} δ : Q × ( Σ ∪ { ε }) ↦ 2 Q
Erweiterte Übergangsfunktion (auch für Leerwort)
δ ∗ \delta^* δ ∗
∀ q ∈ Q : ( q , ε , q ) ∈ δ ∗ \forall q \in Q: (q, \varepsilon, q) \in \delta^{*} ∀ q ∈ Q : ( q , ε , q ) ∈ δ ∗
∃ ( q 1 , w , q 2 ) ∈ δ ∗ , ( q 2 , s , q 3 ) ∈ δ : ( q 1 , w s , q 3 ) ∈ δ ∗
\exists\left(q_{1}, w, q_{2}\right) \in \delta^{*}, \left(q_{2}, s, q_{3}\right) \in \delta: \quad
\left(q_{1}, w s, q_{3}\right) \in \delta^{*}
∃ ( q 1 , w , q 2 ) ∈ δ ∗ , ( q 2 , s , q 3 ) ∈ δ : ( q 1 , w s , q 3 ) ∈ δ ∗ (Transivität)
Akzeptierte / Generierte Sprache
Nur Wörter die von
initial state
zu einem
final state
führen.
L ( A ) = { w ∈ Σ ∗ ∣ ( q 0 , w , q f ) ∈ δ ∗ f u ¨ r ein q f ∈ F }
\mathcal{L}(\mathcal{A})=\left\{w \in \Sigma^{*} \mid\left(q_{0}, w, q_{f}\right) \in \delta^{*} \text { für ein
} q_{f} \in F\right\}
L ( A ) = { w ∈ Σ ∗ ∣ ( q 0 , w , q f ) ∈ δ ∗ f u ¨ r ein q f ∈ F }
Beispiel:
Reelle Numerale mit Exponential-Teil
gültige Beispiele:
3.14
,
0.314E1
,
314.E-2
,...
Vorausgesetzt:
Min 1 Ziffer vor Punkt
Exponentialteil optional (mit E)
mindestens eine Ziffer nach E
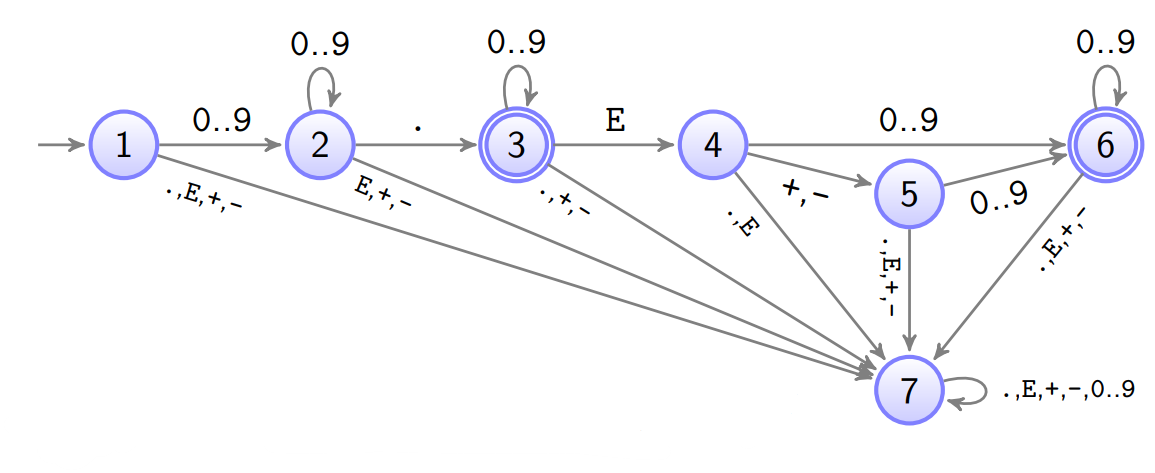
Endlicher (nicht deterministischer Automat)
mit ϵ \epsilon ϵ als Leerwort.
A = ⟨ { 1 , … , 7 } , { 0 , … , 9 , . , E , + , − } , δ , 1 , { 3 , 6 } ⟩
\mathcal{A}=\langle\{1, \ldots, 7\},\{0, \ldots, 9, ., \mathrm{E},+,-\}, \delta, 1,\{3,6\}\rangle
A = ⟨{ 1 , … , 7 } , { 0 , … , 9 , . , E , + , − } , δ , 1 , { 3 , 6 }⟩
L ( A ) = { w ∈ Σ ∗ ∣ ( 1 , w , 3 ) ∈ δ ∗ oder ( 1 , w , 6 ) ∈ δ ∗ }
\mathcal{L}(\mathcal{A})=\left\{w \in \Sigma^{*} \mid(1, w, 3) \in \delta^{*} \text { oder }(1, w,
6) \in \delta^{*}\right\}
L ( A ) = { w ∈ Σ ∗ ∣ ( 1 , w , 3 ) ∈ δ ∗ oder ( 1 , w , 6 ) ∈ δ ∗ }
δ 0 ⋯ 9 . E + − ε 1 { 1 , 2 } ⋯ { 1 , 2 } { } { } { } { } { } 2 { } ⋯ { } { 3 } { } { } { } { } 3 { 3 } ⋯ { 3 } { } { 4 } { } { } { } 4 { } ⋯ { } { } { } { 5 } { 5 } { 5 } 5 { 5 , 6 } ⋯ { 5 , 6 } { } { } { } { } { } 6 { } ⋯ { } { } { } { } { } { }
\begin{array}{c|cccccccc} \delta & 0 & \cdots & 9 & . & \mathrm{E} & +
& - & \varepsilon \\ \hline 1 & \{1,2\} & \cdots & \{1,2\} & \{\} &
\{\} & \{\} & \{\} & \{\} \\ 2 & \{\} & \cdots & \{\} & \{3\} &
\{\} & \{\} & \{\} & \{\} \\ 3 & \{3\} & \cdots & \{3\} & \{\} &
\{4\} & \{\} & \{\} & \{\} \\ 4 & \{\} & \cdots & \{\} & \{\} &
\{\} & \{5\} & \{5\} & \{5\} \\ 5 & \{5,6\} & \cdots & \{5,6\} &
\{\} & \{\} & \{\} & \{\} & \{\} \\ 6 & \{\} & \cdots & \{\} &
\{\} & \{\} & \{\} & \{\} & \{\} \end{array}
δ
1 2 3 4 5 6 0 { 1 , 2 } { } { 3 } { } { 5 , 6 } { } ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ 9 { 1 , 2 } { } { 3 } { } { 5 , 6 } { } . { } { 3 } { } { } { } { } E { } { } { 4 } { } { } { } + { } { } { } { 5 } { } { } − { } { } { } { 5 } { } { } ε { } { } { } { 5 } { } { }
Determinisierung (NEA
→ \rarr → Gegeben: NEA
A = ⟨ Q , Σ , δ , q 0 , F ⟩
\mathcal{A}=\left\langle Q, \Sigma, \delta, q_{0}, F\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩ (A steht für Automat)
δ ⊆ Q × ( Σ ∪ { ε } ) × Q \delta \subseteq Q \times(\Sigma \cup\{\varepsilon\}) \times Q δ ⊆ Q × ( Σ ∪ { ε }) × Q
Gesucht: DEA
A undefined = ⟨ Q undefined , Σ , δ undefined , q 0 undefined , F undefined ⟩
\widehat{\mathcal{A}}=\left\langle\widehat{Q}, \Sigma, \widehat{\delta}, \widehat{q_{0}},
\widehat{F}\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩
δ undefined : Q undefined × Σ ↦ Q undefined
\widehat{\delta}: \widehat{Q} \times \Sigma \mapsto \widehat{Q}
δ : Q × Σ ↦ Q
Unter der Bedingung dass
A ^ \mathcal{\hat{A}} A ^ A \mathcal{A} A L ( A ) = L ( A undefined ) \mathcal{L}(\mathcal{A})=\mathcal{L}(\widehat{\mathcal{A}}) L ( A ) = L ( A )
Definition von DEA A undefined \mathcal{\widehat{A}} A
Q undefined = 2 Q \widehat{Q}=2^{Q} Q = 2 Q (Potenzmenge von Q Q Q - Alle Teilmengen / Zustands-Wörter)
q 0 undefined = { q 0 } \widehat{q_{0}}=\left\{q_{0}\right\} q 0 = { q 0 } (Klammern stehen nicht für Menge)
F undefined = { { q undefined ∈ Q undefined ∣ q undefined ∩ F ≠ ∅ } ∪ { q 0 undefined } falls ε ∈ L ( A ) { q undefined ∈ Q undefined ∣ q undefined ∩ F ≠ ∅ } sonst
\widehat{F}=\left\{\begin{array}{ll}\{\widehat{q} \in \widehat{Q} \mid \widehat{q} \cap F \neq \emptyset\}
\cup\left\{\widehat{q_{0}}\right\} & \text { falls } \varepsilon \in \mathcal{L}(\mathcal{A})
\\\{\widehat{q} \in \widehat{Q} \mid \widehat{q} \cap F \neq \emptyset\} & \text { sonst }\end{array}\right.
F = { {
q
∈ Q ∣
q
∩ F = ∅ } ∪ {
q
0
} {
q
∈ Q ∣
q
∩ F = ∅ } falls ε ∈ L ( A ) sonst
Unsere finalen Zustände sind alle Zustands-Wörter / Mengen die bei einem Durchschnitt mit dem Zustand
F F F nicht leer sind → Die den Buchstaben F F F enthalten.
Falls Leerwörter erlaubt sind muss der Anfangszustand auch enthalten sein.
∀ q undefined ∈ Q , s ∈ ∑ : \forall \widehat{q} \in Q, s\in \sum : ∀ q ∈ Q , s ∈ ∑ :
δ undefined ( q undefined , s ) = { q ′ ∈ Q ∣ ∃ q ∈ q undefined , sodass ( q , s , q ′ ) ∈ δ ∗ }
\widehat{\delta}(\widehat{q}, s)=\left\{q^{\prime} \in Q \mid \exists q \in \widehat{q}, \text { sodass
}\left(q, s, q^{\prime}\right) \in \delta^{*}\right\}
δ ( q , s ) = { q ′ ∈ Q ∣ ∃ q ∈ q , sodass ( q , s , q ′ ) ∈ δ ∗ }
bzw
δ undefined ( q undefined , s ) = ⋃ q ∈ q undefined { q ′ ∈ Q ∣ ( q , s , q ′ ) ∈ δ ∗ } = ⋃ q ∈ q undefined δ ∗ ( q , s )
\widehat{\delta}(\widehat{q}, s)=\bigcup_{q \in \widehat{q}}\left\{q^{\prime} \in Q \mid\left(q, s,
q^{\prime}\right) \in \delta^{*}\right\}=\bigcup_{q \in \widehat{q}} \delta^{*}(q, s)
δ ( q , s ) = ⋃ q ∈
q
{ q ′ ∈ Q ∣ ( q , s , q ′ ) ∈ δ ∗ } = ⋃ q ∈
q
δ ∗ ( q , s )
Die Übergangsfunktion:
Q × s ∈ ∑ ↦ { … } Q \times s\in\sum \mapsto \{ \dots\} Q × s ∈ ∑ ↦ { … }
Bildet jeden Zustand mit Symbol auf einem Wort, dass alle Folgezustände enthält
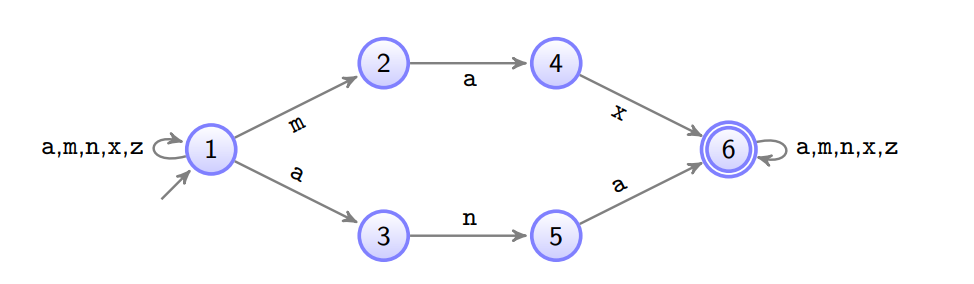
Beispiel:
Suche nach "max" und "ana" Dadurch, dass es keine ϵ \epsilon ϵ gibt ist Tabelle von δ \delta δ gleich mit δ ∗ \delta^* δ ∗
Anfangszustand ist
1 1 1 6 6 6
δ ∗ a m n x z 1 { 1 , 3 } { 1 , 2 } { 1 } { 1 } { 1 } 2 { 4 } { } { } { } { } 3 { } { } { 5 } { } { } 4 { } { } { } { 6 } { } 5 { 6 } { } { } { } { } 6 { 6 } { 6 } { 6 } { 6 } { 6 }
\begin{array}{c|ccccc}\delta^{*} & \mathrm{a} & \mathrm{m} & \mathrm{n} &
\mathrm{x} & \mathrm{z} \\\hline 1 & \{1,3\} & \{1,2\} & \{1\} & \{1\} &
\{1\} \\2 & \{4\} & \{\} & \{\} & \{\} & \{\} \\3 & \{\} & \{\}
& \{5\} & \{\} & \{\} \\4 & \{\} & \{\} & \{\} & \{6\} & \{\}
\\5 & \{6\} & \{\} & \{\} & \{\} & \{\} \\6 & \{6\} & \{6\} &
\{6\} & \{6\} & \{6\}\end{array}
δ
∗
1 2 3 4 5 6 a { 1 , 3 } { 4 } { } { } { 6 } { 6 } m { 1 , 2 } { } { } { } { } { 6 } n { 1 } { } { 5 } { } { } { 6 } x { 1 } { } { } { 6 } { } { 6 } z { 1 } { } { } { } { } { 6 }
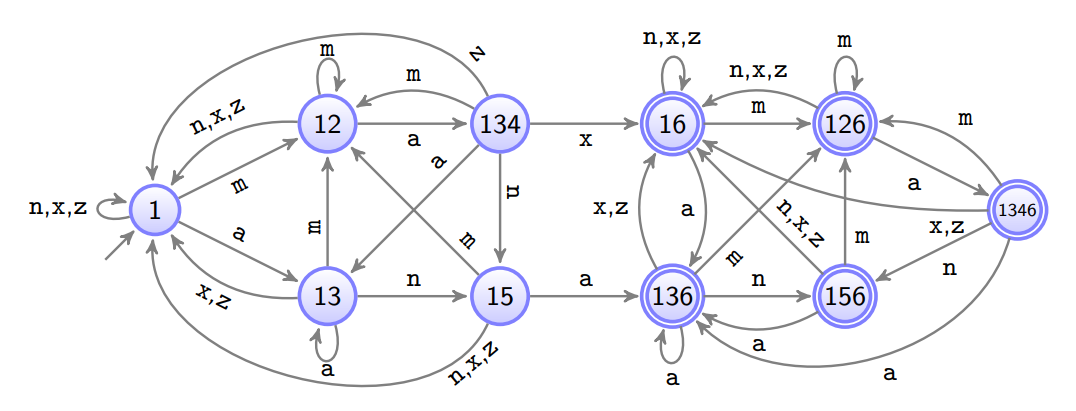
Wir definieren eine
δ undefined \widehat{\delta} δ
Anfangszustand ist
1 1 1 1 1 1 6 6 6
Wichtig: die Tabelleneinträge sind keine Mengen sondern Wörter obwohl wir {} benutzen.
δ undefined a m n x z { 1 } { 1 , 3 } { 1 , 2 } { 1 } { 1 } { 1 } { 1 , 2 } { 1 , 3 , 4 } { 1 , 2 } { 1 } { 1 } { 1 } { 1 , 3 } { 1 , 3 } { 1 , 2 } { 1 , 5 } { 1 } { 1 } { 1 , 3 , 4 } { 1 , 3 } { 1 , 2 } { 1 , 5 } { 1 , 6 } { 1 } { 1 , 5 } { 1 , 3 , 6 } { 1 , 2 } { 1 } { 1 } { 1 } { 1 , 6 } { 1 , 3 , 6 } { 1 , 2 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 3 , 6 } { 1 , 3 , 6 } { 1 , 2 , 6 } { 1 , 5 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 2 , 6 } { 1 , 3 , 4 , 6 } { 1 , 2 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 5 , 6 } { 1 , 3 , 6 } { 1 , 2 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 3 , 4 , 6 } { 1 , 3 , 6 } { 1 , 2 , 6 } { 1 , 5 , 6 } { 1 , 6 } { 1 , 6 }
\begin{array}{c|ccccc}\widehat{\delta} & \mathrm{a} & \mathrm{m} & \mathrm{n} &
\mathrm{x} & \mathrm{z} \\\hline\{1\} & \{1,3\} & \{1,2\} & \{1\} & \{1\} &
\{1\} \\\{1,2\} & \{1,3,4\} & \{1,2\} & \{1\} & \{1\} & \{1\} \\\{1,3\} &
\{1,3\} & \{1,2\} & \{1,5\} & \{1\} & \{1\} \\\{1,3,4\} & \{1,3\} & \{1,2\}
& \{1,5\} & \{1,6\} & \{1\} \\\{1,5\} & \{1,3,6\} & \{1,2\} & \{1\} &
\{1\} & \{1\} \\\{1,6\} & \{1,3,6\} & \{1,2,6\} & \{1,6\} & \{1,6\} &
\{1,6\} \\\{1,3,6\} & \{1,3,6\} & \{1,2,6\} & \{1,5,6\} & \{1,6\} & \{1,6\}
\\\{1,2,6\} & \{1,3,4,6\} & \{1,2,6\} & \{1,6\} & \{1,6\} & \{1,6\} \\\{1,5,6\}
& \{1,3,6\} & \{1,2,6\} & \{1,6\} & \{1,6\} & \{1,6\} \\\{1,3,4,6\} &
\{1,3,6\} & \{1,2,6\} & \{1,5,6\} & \{1,6\} & \{1,6\}\end{array}
δ
{ 1 } { 1 , 2 } { 1 , 3 } { 1 , 3 , 4 } { 1 , 5 } { 1 , 6 } { 1 , 3 , 6 } { 1 , 2 , 6 } { 1 , 5 , 6 } { 1 , 3 , 4 , 6 } a { 1 , 3 } { 1 , 3 , 4 } { 1 , 3 } { 1 , 3 } { 1 , 3 , 6 } { 1 , 3 , 6 } { 1 , 3 , 6 } { 1 , 3 , 4 , 6 } { 1 , 3 , 6 } { 1 , 3 , 6 } m { 1 , 2 } { 1 , 2 } { 1 , 2 } { 1 , 2 } { 1 , 2 } { 1 , 2 , 6 } { 1 , 2 , 6 } { 1 , 2 , 6 } { 1 , 2 , 6 } { 1 , 2 , 6 } n { 1 } { 1 } { 1 , 5 } { 1 , 5 } { 1 } { 1 , 6 } { 1 , 5 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 5 , 6 } x { 1 } { 1 } { 1 } { 1 , 6 } { 1 } { 1 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 6 } z { 1 } { 1 } { 1 } { 1 } { 1 } { 1 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 6 } { 1 , 6 }
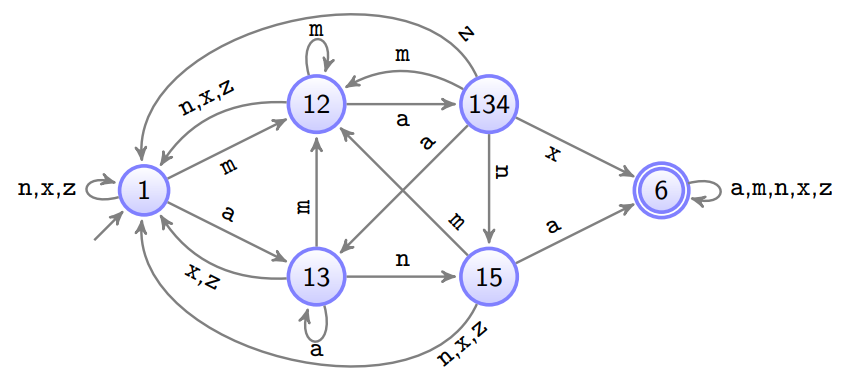
Da von den Endzuständen keine Kanten zurückführen und man somit den Endzustand nicht verlässt: kürzen möglich.
Endlicher Transducer
Automat beschrieben durch
A = ⟨ Q , Σ , Γ , δ , I , F ⟩ \mathcal{A}=\langle Q, \Sigma, \Gamma, \delta, I, F\rangle A = ⟨ Q , Σ , Γ , δ , I , F ⟩
Menge an Anfangszuständen
Γ \Gamma Γ output alphabet
δ ⊆ Q × ( Σ ∪ { ε } ) × ( Γ ∪ { ε } ) × Q
\delta \subseteq Q \times(\Sigma \cup\{\varepsilon\}) \times(\Gamma \cup\{\varepsilon\}) \times Q
δ ⊆ Q × ( Σ ∪ { ε }) × ( Γ ∪ { ε }) × Q
I ⊆ Q I \subseteq Q I ⊆ Q initial states
Erweiterte Übergangsrelation (auch für Leerwort)
δ ∗ ⊆ Q × Σ ∗ × Γ ∗ × Q
\delta^{*} \subseteq Q \times \Sigma^{*} \times \Gamma^{*} \times Q
δ ∗ ⊆ Q × Σ ∗ × Γ ∗ × Q
δ ∗ \delta^* δ ∗
∀ q ∈ Q : ( q , ε , ε , q ) ∈ δ ∗
\forall q \in Q: (q, \varepsilon, \varepsilon, q) \in \delta^{*}
∀ q ∈ Q : ( q , ε , ε , q ) ∈ δ ∗
( q 1 , w , w ′ , q 2 ) ∈ δ ∗ , ( q 2 , s , s ′ , q 3 ) ∈ δ ⟹ ( q 1 , w s , w ′ s ′ , q 3 ) ∈ δ ∗
\left(q_{1}, w, w^{\prime}, q_{2}\right) \in \delta^{*},\left(q_{2}, s, s^{\prime}, q_{3}\right) \in \delta
\quad \Longrightarrow \quad\left(q_{1}, w s, w^{\prime} s^{\prime}, q_{3}\right) \in \delta^{*}
( q 1 , w , w ′ , q 2 ) ∈ δ ∗ , ( q 2 , s , s ′ , q 3 ) ∈ δ ⟹ ( q 1 , w s , w ′ s ′ , q 3 ) ∈ δ ∗
Übersetzungsrelation
Automat generiert nicht mehr Sprache sondern gibt uns eine Übersetzungsrelation (zu jedem Eingabewort, ein Ausgabewort)
[ A ] = { ( w , w ′ ) ∈ Σ ∗ × Γ ∗ ∣ ∀ i ∈ I , f ∈ F : ( i , w , w ′ , f ) ∈ δ ∗ }
[\mathcal{A}]=\left\{\left(w, w^{\prime}\right) \in \Sigma^{*} \times \Gamma^{*} \mid \forall i \in I, f \in F:
\left (i, w, w^{\prime}, f\right) \in \delta^{*} \right\}
[ A ] = { ( w , w ′ ) ∈ Σ ∗ × Γ ∗ ∣ ∀ i ∈ I , f ∈ F : ( i , w , w ′ , f ) ∈ δ ∗ }
[ A ] ⊆ Σ ∗ × Γ ∗ [\mathcal{A}] \subseteq \Sigma^{*} \times \Gamma^{*} [ A ] ⊆ Σ ∗ × Γ ∗
Beispiele:
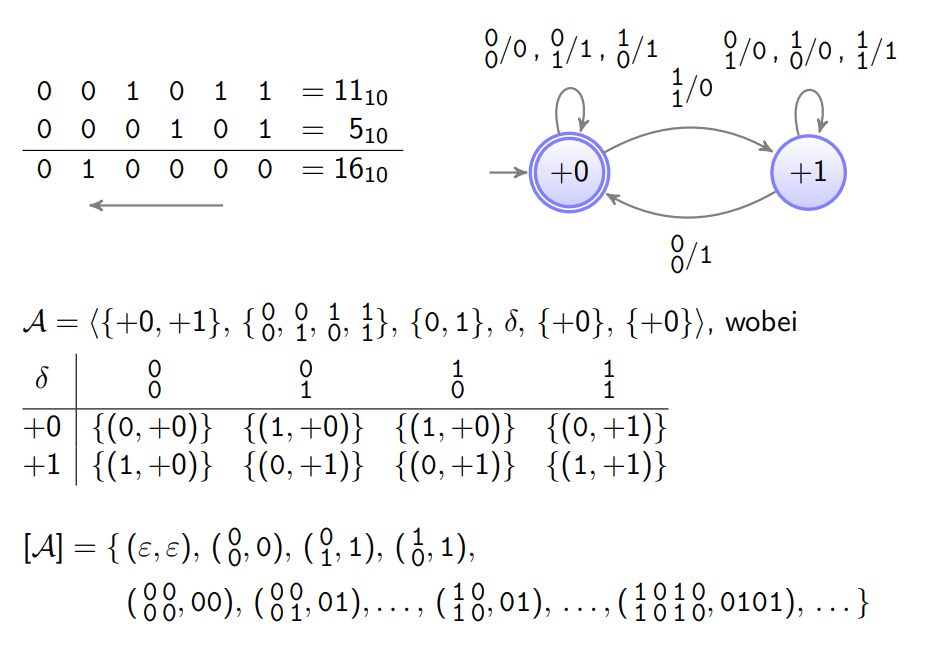
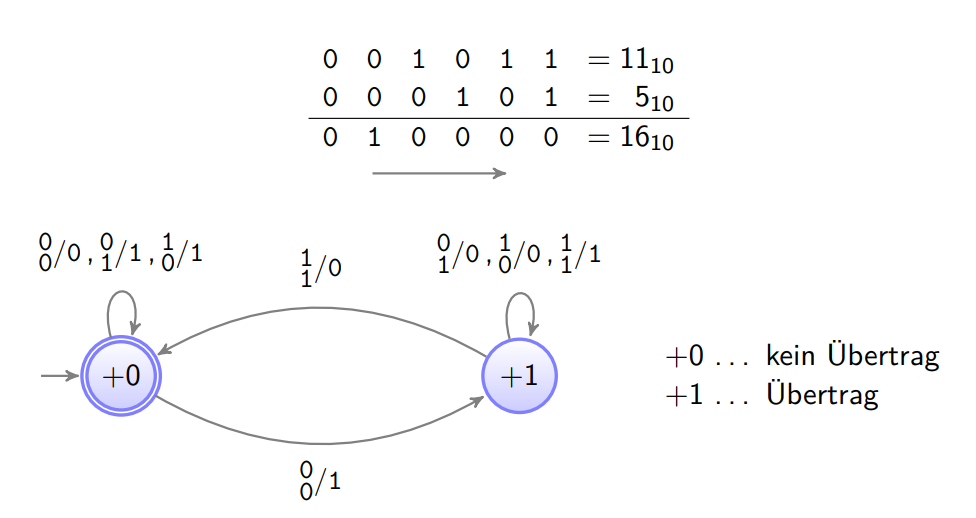
Binäraddition von R nach L (deterministisch) Binäraddition von L nach R (nicht deterministisch)
Mealy-Automat Art von Transducer, deterministisch
Ausgabe mit
Eingabe
verknüpft
Nur ein Anfangszustand
I = { q 0 } I=\left\{q_{0}\right\} I = { q 0 }
Alle Zustände sind Endzustände
F = Q F = Q F = Q
Keine
ε \varepsilon ε
Automat beschrieben durch
A = ⟨ Q , Σ , Γ , δ , γ , q 0 ⟩
\mathcal{A}=\left\langle Q, \Sigma, \Gamma, \delta, \gamma, q_{0}\right\rangle
A = ⟨ Q , Σ , Γ , δ , γ , q 0 ⟩
Γ \Gamma Γ output alphabet
γ : Q × Σ ↦ Γ \gamma: Q \times \Sigma \mapsto \Gamma γ : Q × Σ ↦ Γ output function
/ Ausgabefunktion
Bildet Relations-Tupel → Zu jeder Eingabe und jedem Zustand eine Ausgabe ( q , s , γ ( q , s ) , δ ( q , s ) ) (q, s, \gamma(q, s), \delta(q, s)) ( q , s , γ ( q , s ) , δ ( q , s ))
Erweiterte Ausgabefunktion (auch für Leerwort)
γ ∗ : Q × Σ ∗ ↦ Γ ∗ \gamma^{*}: Q \times \Sigma^{*} \mapsto \Gamma^{*} γ ∗ : Q × Σ ∗ ↦ Γ ∗
∀ q ∈ Q , s ∈ Σ , w ∈ Σ ∗ : \forall q \in Q, s \in \Sigma, w \in \Sigma^{*}: ∀ q ∈ Q , s ∈ Σ , w ∈ Σ ∗ :
γ ∗ ( q , ε ) = ε \gamma^{*}(q, \varepsilon)=\varepsilon γ ∗ ( q , ε ) = ε
γ ∗ ( q , s w ) = γ ( q , s ) ⋅ γ ∗ ( δ ( q , s ) , w )
\gamma^{*}(\textcolor{pink}q, s w)=\gamma(q, s) \cdot \gamma^{*}(\textcolor{pink}{\delta(q, s)}, w)
γ ∗ ( q , s w ) = γ ( q , s ) ⋅ γ ∗ ( δ ( q , s ) , w )
Übersetzungsfunktion
[ A ] ( w ) = γ ∗ ( q 0 , w ) [\mathcal{A}](w)=\gamma^{*}\left(q_{0}, w\right) [ A ] ( w ) = γ ∗ ( q 0 , w )
[ A ] : Σ ∗ ↦ Γ ∗ [\mathcal{A}]: \Sigma^{*} \mapsto \Gamma^{*} [ A ] : Σ ∗ ↦ Γ ∗
Beispiel:
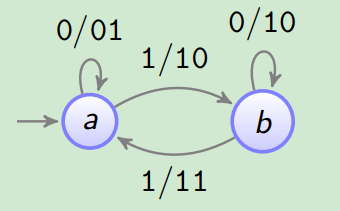
(1:2)-(0,1)-RLL Encoder A = ⟨ { a , b } , { 0 , 1 } , { 01 , 10 , 11 } , δ , γ , a ⟩
\mathcal{A}=\langle\{a, b\},\{0,1\},\{01,10,11\}, \delta, \gamma, a\rangle
A = ⟨{ a , b } , { 0 , 1 } , { 01 , 10 , 11 } , δ , γ , a ⟩
δ 0 1 a a b b b a
\begin{array}{c|cc}\delta & 0 & 1 \\\hline a & a & b \\b & b & a\end{array}
δ
a b 0 a b 1 b a γ 0 1 a 01 10 b 10 11
\begin{array}{l|cc}\gamma & 0 & 1 \\\hline a & 01 & 10 \\b & 10 &
11\end{array}
γ
a b 0 01 10 1 10 11
w : ε 0 1 00 10 01 11 000 100 ⋯ [ A ] ( w ) : ε 01 10 0101 1010 0110 1011 010101 101010 ⋯
\begin{array}{rllllllllllll}w: & \varepsilon & 0 & 1 & 00 & 10 & 01 & 11
& 000 & 100 & \cdots \\\hline[\mathcal{A}](w): & \varepsilon & 01 & 10 &
0101 & 1010 & 0110 & 1011 & 010101 & 101010 & \cdots\end{array}
w
: [ A ] (
w
) : ε ε 0 01 1 10 00 0101 10 1010 01 0110 11 1011 000 010101 100 101010 ⋯ ⋯
Moore-Automat Art von Transducer (technisch gesehen aber nicht), deterministisch
Ausgabe mit
Zustand
verknüpft
Nur ein Anfangszustand
I = { q 0 } I=\left\{q_{0}\right\} I = { q 0 }
Alle Zustände sind Endzustände
F = Q F = Q F = Q
Keine
ε \varepsilon ε
Automat beschrieben durch
A = ⟨ Q , Σ , Γ , δ , γ , q 0 ⟩
\mathcal{A}=\left\langle Q, \Sigma, \Gamma, \delta, \gamma, q_{0}\right\rangle
A = ⟨ Q , Σ , Γ , δ , γ , q 0 ⟩
Г \text { Г } Г output alphabet
γ : Q ↦ Γ \gamma: Q \mapsto \Gamma γ : Q ↦ Γ output function (bei Mealy: γ : Q × Σ ↦ Γ \gamma: Q \times \Sigma \mapsto \Gamma γ : Q × Σ ↦ Γ )
Erweiterte Ausgabefunktion (auch für Leerwort)
γ ∗ : Q × Σ ∗ ↦ Γ ∗ \gamma^{*}: Q \times \Sigma^{*} \mapsto \Gamma^{*} γ ∗ : Q × Σ ∗ ↦ Γ ∗
∀ q ∈ Q , s ∈ Σ , w ∈ Σ ∗ : \forall q \in Q, s \in \Sigma, w \in \Sigma^{*}: ∀ q ∈ Q , s ∈ Σ , w ∈ Σ ∗ :
γ ∗ ( q , ε ) = ε \gamma^{*}(q, \varepsilon)=\varepsilon γ ∗ ( q , ε ) = ε
γ ∗ ( q , s w ) = γ ( q ) ⋅ γ ∗ ( δ ( q , s ) , w )
\gamma^{*}(q, s w)=\gamma(q) \cdot \gamma^{*}(\delta(q, s), w)
γ ∗ ( q , s w ) = γ ( q ) ⋅ γ ∗ ( δ ( q , s ) , w )
γ ∗ ( q , s w ) = γ ( q , s ) ⋅ γ ∗ ( δ ( q , s ) , w )
\gamma^{*}(q, s w)=\gamma(q, s) \cdot \gamma^{*}(\delta(q, s), w)
γ ∗ ( q , s w ) = γ ( q , s ) ⋅ γ ∗ ( δ ( q , s ) , w )
Übersetzungsfunktion (gleich wie Mealy)
[ A ] ( w ) = γ ∗ ( q 0 , w ) [\mathcal{A}](w)=\gamma^{*}\left(q_{0}, w\right) [ A ] ( w ) = γ ∗ ( q 0 , w )
[ A ] : Σ ∗ ↦ Γ ∗ [\mathcal{A}]: \Sigma^{*} \mapsto \Gamma^{*} [ A ] : Σ ∗ ↦ Γ ∗
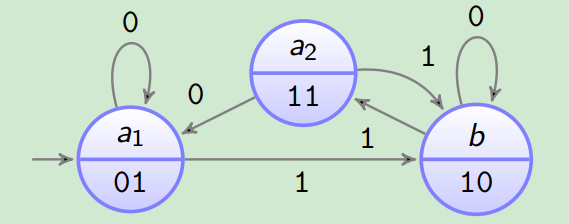
Beispiel:
(1:2)-(0,1)-RLL Encoder A = ⟨ { a , b } , { 0 , 1 } , { 01 , 10 , 11 } , δ , γ , a ⟩
\mathcal{A}=\langle\{a, b\},\{0,1\},\{01,10,11\}, \delta, \gamma, a\rangle
A = ⟨{ a , b } , { 0 , 1 } , { 01 , 10 , 11 } , δ , γ , a ⟩ bei Mealy
A = ⟨ { a 1 , a 2 , b } , { 0 , 1 } , { 01 , 10 , 11 } , δ , γ , a ⟩
\mathcal{A}=\left\langle\left\{a_{1}, a_{2}, b\right\},\{0,1\},\{01,10,11\}, \delta, \gamma,
a\right\rangle
A = ⟨ { a 1 , a 2 , b } , { 0 , 1 } , { 01 , 10 , 11 } , δ , γ , a ⟩
δ 0 1 a 1 a 1 b a 2 a 1 b b b a 2
\begin{array}{c|cc}\delta & 0 & 1 \\\hline a_{1} & a_{1} & b \\a_{2} & a_{1}
& b \\b & b & a_{2}\end{array}
δ
a
1
a
2
b 0 a
1
a
1
b 1 b b a
2
γ a 1 01 a 2 11 b 10
\begin{array}{c|c}\gamma & \\\hline a_{1} & 01 \\a_{2} & 11 \\b & 10\end{array}
γ
a
1
a
2
b 01 11 10
Büchi-Automaten Deterministisch
Automat beschrieben durch
A = ⟨ Q , Σ , δ , q 0 , F ⟩
\mathcal{A}=\left\langle Q, \Sigma, \delta, q_{0}, F\right\rangle
A = ⟨ Q , Σ , δ , q 0 , F ⟩ (alles gleich wie in DEAs definiert)
Akzeptanz von Wörtern
Wort
s 1 s 2 s 3 ⋯ ∈ ∑ ω s_{1} s_{2} s_{3} \cdots \in \sum^\omega s 1 s 2 s 3 ⋯ ∈ ∑ ω q 0 , q 1 , q 2 , q 3 , ⋯ ∈ Q q_{0}, q_{1}, q_{2}, q_{3}, \cdots \in Q q 0 , q 1 , q 2 , q 3 , ⋯ ∈ Q
q 0 ∈ Q q_{0} \in Q q 0 ∈ Q ∀ i ∈ N : δ ( q i − 1 , s i ) = q i \forall i \in \N: \delta\left(q_{i-1}, s_{i}\right)=q_{i} ∀ i ∈ N : δ ( q i − 1 , s i ) = q i lim i → ∞ \lim_{i\to\infty} lim i → ∞ q i ∈ F q_{i} \in F q i ∈ F (Endzustand ist ein "guter Zustand", kein Deadlock)
Akzeptierte/Generierte Sprache
L ( A ) = { w ∈ Σ ω ∣ w wird von A akzeptiert }
\mathcal{L}(\mathcal{A})=\left\{w \in \Sigma^{\omega} \mid w \text { wird von } \mathcal{A} \text { akzeptiert
}\right\}
L ( A ) = { w ∈ Σ ω ∣ w wird von A akzeptiert }
Beispiel:
Anwendung: in Programmen die liveliness property feststellen - Programm darf nicht absterben
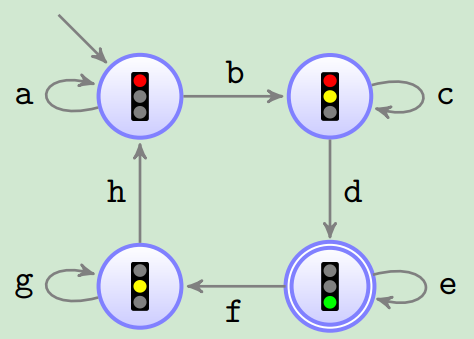
Faire Verkehrsampel
Es werden die wörter aus
{ a , … , h } ω \{\texttt{a}, \ldots, \texttt{h}\}^{\omega} { a , … , h }
ω
Nicht-Deterministisch
Automat beschrieben durch
A = ⟨ Q , Σ , δ , I , F ⟩ \mathcal{A}=\langle Q, \Sigma, \delta, I, F\rangle A = ⟨ Q , Σ , δ , I , F ⟩
I ⊆ Q I \subseteq Q I ⊆ Q
δ ⊆ Q × Σ × Q \delta \subseteq Q \times \Sigma \times Q δ ⊆ Q × Σ × Q
Akzeptanz von Wörtern
Wort
s 1 s 2 s 3 ⋯ ∈ Σ ω s_{1} s_{2} s_{3} \cdots \in \Sigma^\omega s 1 s 2 s 3 ⋯ ∈ Σ ω q 0 , q 1 , q 2 , q 3 , ⋯ ∈ Q q_{0}, q_{1}, q_{2}, q_{3}, \cdots \in Q q 0 , q 1 , q 2 , q 3 , ⋯ ∈ Q
q 0 ∈ Q , q 0 ∈ I q_{0} \in Q, \space q_0 \in I q 0 ∈ Q , q 0 ∈ I
∀ i ∈ N : δ ( q i − 1 , s i ) = q i \forall i \in \N: \delta\left(q_{i-1}, s_{i}\right)=q_{i} ∀ i ∈ N : δ ( q i − 1 , s i ) = q i
lim i → ∞ \lim_{i\to\infty} lim i → ∞ q i ∈ F q_{i} \in F q i ∈ F
Akzeptierte/Generierte Sprache
L ( A ) = { w ∈ Σ ω ∣ w wird von A akzeptiert }
\mathcal{L}(\mathcal{A})=\left\{w \in \Sigma^{\omega} \mid w \text { wird von } \mathcal{A} \text { akzeptiert
}\right\}
L ( A ) = { w ∈ Σ ω ∣ w wird von A akzeptiert }
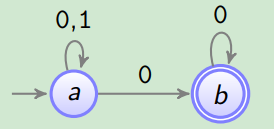
Beispiel:
Nur endlich viele 1er Ein Büchi-Automat, der genau jene ω-Wörter über {0, 1} akzeptiert, die nur eine endliche Anzahl an 1ern enthalten.
(wird nur von deterministischen akzeptiert)
Modellierung 📌
Modellierung durch endlichen Automaten